Анализ размерностей представляет собой общий метод, позволяющий с точностью до безразмерной константы получить выражение для нужной физической величины, размерность которой нам известна. Для этого выбираются «базовые» величины, ни одна из которых не может быть выражена через остальные. Их комбинация и даст интересующий результат. Анализ размерностей приводит к оценке по порядку величины, причём иногда получаются точные аналитические выражения.
В качестве примера приведём доказательство теоремы Пифагора. Рассмотрим прямоугольный треугольник с катетами a и b и гипотенузой c:

Острый угол напротив стороны a обозначим A. Из соображений размерности площадь треугольника S пропорциональна квадрату одной из сторон, скажем, гипотенузы:
![]()
Высота h, опущенная из прямого угла на гипотенузу, разбивает треугольник на два ему подобных, причём их гипотенузы равны a и b соответственно. Острый угол каждого из этих треугольников равен A, поэтому их площади могут быть выражены как
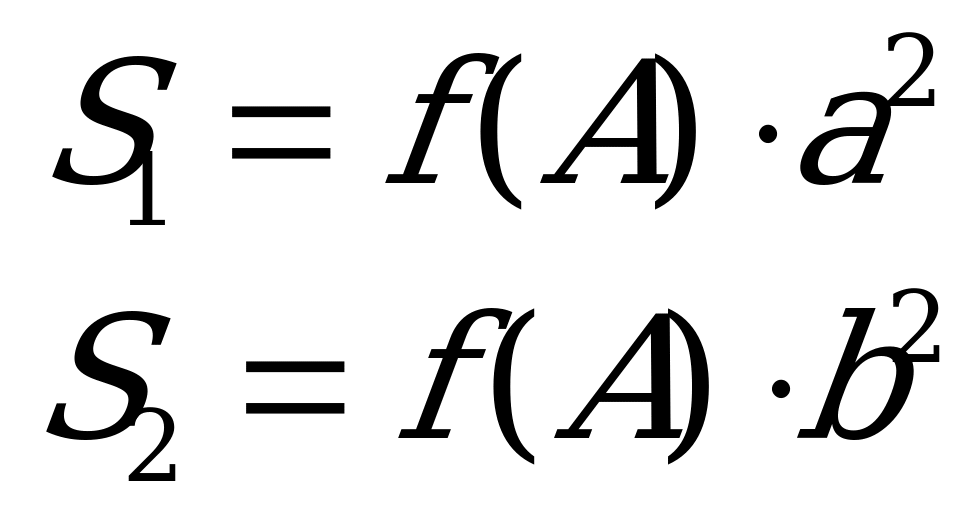 .
.
Подставляя эти формулы в очевидное равенство
![]()
и сокращая на общий множитель f(A), приходим к искомой теореме:
![]()
Перейдём к физическим приложениям.
В предлагаемом курсе мы будем пользоваться, главным образом, симметричной, или гауссовой системой единиц. В ней электрические величины измеряются в единицах СГСЭ, а магнитные — в единицах СГСМ. Лишь в отдельных случаях мы будем употреблять систему СИ, специально это оговорив, а там, где это уместно — и внесистемные единицы, такие как электрон–вольт (эВ) или ридберг (Ry). Применяемые значения констант взяты из статьи “The Fundamental Physical Constants”, опубликованной на странице 9 журнала “Physics Today” Volume 49, Number 8, Part 2, авторы — E. Richard Cohen и Barry N. Taylor.
Итак, массу мы измеряем в граммах (г), размеры — в сантиметрах (см) и время — в секундах (с). В качестве базовых величин возьмем элементарный электрический заряд e, массу электрона me и скорость света c:
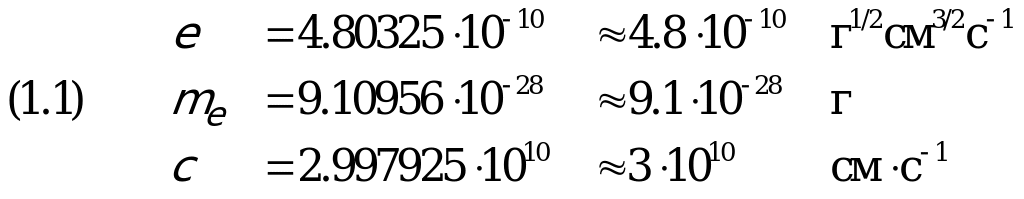
Это — экспериментальные величины, не определяемые теоретически.
Классический радиус электрона.Сформируем имеющую размерность длины комбинацию для релятивистской, но не квантовой величины: в ней должна присутствовать скорость света, но нет постоянной Планка. Для этого составим уравнение вида
![]()
Для размерностей это выглядит так:
![]()
Приравняв степени при одинаковых единицах размерности в левой и правой частях последней формулы, получим систему из трех линейных уравнений:
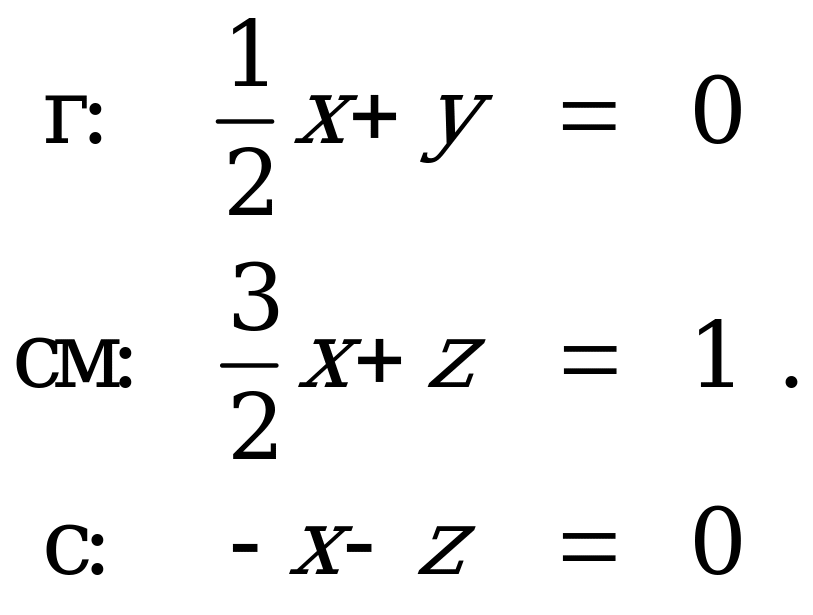
Решение этой системы дает:
x = 2, y = –1, z = –2.
Таким образом, комбинация базовых величин (1.1) с размерностью длины имеет вид:
![]()
Мы получили выражение для так называемого классического радиуса электрона re. Численно он равен
re=2.82·10–13 см.
Перепишем формулу для re в виде
![]()
В правой части последнего уравнения стоит кулоновская энергия взаимодействия зарядов e, находящихся на расстоянии re, а в левой части — энергия покоящегося электрона. Таким образом, re представляет собой такой размер шарика с зарядом e, при котором энергия взаимодействия электрона с возбуждаемым им полем равна его энергии покоя mec2.
В атомной физике энергию часто выражают в электронвольтах (эВ). Такую энергию приобретает электрон после прохождения разности потенциалов, равной одному вольту. Напомним, что вольт — это единица измерения разности потенциалов в системе СИ, она примерно в триста раз меньше соответствующей единицы гауссовой системы:
![]()
Отсюда вытекает связь между электронвольтом и эргом — единицей энергии в системе Гаусса:
1 эВ = 1.602192·10-12 эрг ≈ 1.6·10-12 эрг.
Хотя для температуры принята своя единица измерения — градус Кельвина, тем не менее, и здесь иногда прибегают к электрон–вольтам. Чтобы выразить температуру в энергетических единицах, надо выполнить замену
![]()
где k — постоянная Больцмана,
![]()
Отсюда легко вычислить температуру, соответствующую одному электронвольту:
1эВ=11604.55 K.
Выразим энергию покоя электрона в электронвольтах:
![]()
Известна реакция образования электрон-позитронных пар — превращение гамма–кванта (γ) в электрон (e–) и позитрон (e+):
![]()
Позитрон — это элементарная частица, масса которой равна массе электрона; заряды электрона и позитрона равны по абсолютной величине, но противоположны по знаку. Говорят, что позитрон является античастицей по отношению к электрону. Пороговая энергия реакции определяется суммарной энергией покоя электрона и позитрона и составляет около одного мегаэлектронвольта. Имеет место и обратная реакция — аннигиляция электрона и позитрона:
![]()
В этой реакции возникают два или три фотона.
Другая важная для атомной физики частица — протон относится к классу нуклонов. Нуклон — это обобщённое наименование протона и нейтрона, частиц, из которых состоит ядро атома. Протон значительно тяжелее электрона:
mp = 1836.11·me= 1.672661·10-24 г.
Энергия покоя протона mpc2 равна 938 МэВ. Нейтрон слегка тяжелее протона, его масса равна 1.6750·10-24 г, а соответствующая ему энергия покоя составляет 940 МэВ. Аннигиляция нуклона и антинуклона чаще всего приводит к образованию π–мезонов.

 Получите свидетельство
Получите свидетельство Вход
Вход











 Анализ размерностей. (67 KB)
Анализ размерностей. (67 KB)
 0
0 249
249 0
0 Нравится
0
Нравится
0



