Анализ графиков. Подготовка к ЕГЭ по профильной математике

Анализ графиков функций

Задание № 11

Анализ графиков функций

• Линейная функция
• Квадратичная функция
• Степенная функция
• Показательная и логарифмическая функция
• Тригонометрические функции
• Кусочно-линейная функция
• Комбинированные задачи

Прототипы заданий

• Найти аргумент по известному значению функции
• Найти значение функции по известному значению аргумента
• Найти координаты вершины параболы
• Найти точку пересечения графиков двух функций
• Найти один из параметров
• Найти решение уравнения

Линейная функция. График - прямая

b = f(0)

b = f(0)

Прямые перпендикулярны тогда, когда произведение их угловых коэффициентов равно -1

Прямые параллельны тогда, когда их угловые коэффициенты равны

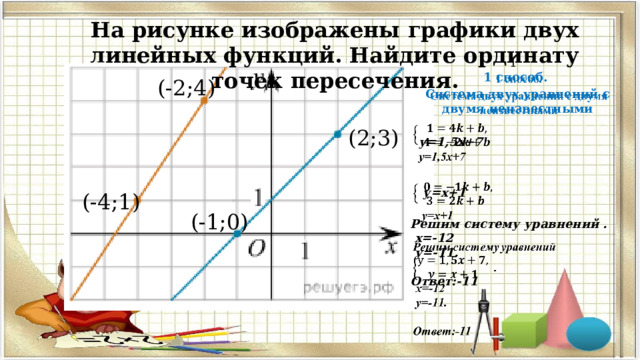
На рисунке изображены графики двух линейных функций. Найдите ординату точек пересечения.

1

1 способ.

Система двух уравнений с двумя неизвестными

у=1,5х+7

у=х+1

Решим систему уравнений .

х=-12

у=-11.

Ответ:-11

(-2;4)

(2;3)

(-4;1)

(-1;0)

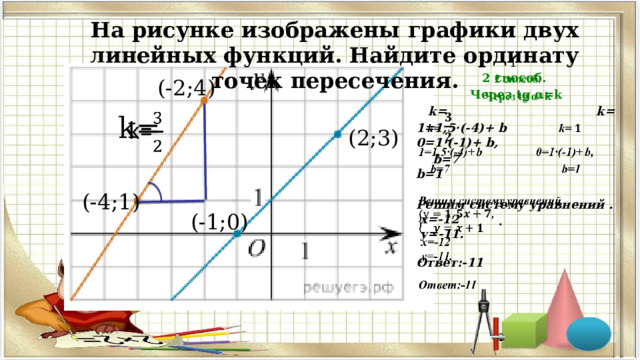
На рисунке изображены графики двух линейных функций. Найдите ординату точек пересечения.

1

2 способ.

Через tg α=k

k= k=

1=1,5·(-4)+ b 0=1·(-1)+ b,

b=7 b=1

Решим систему уравнений .

х=-12

у=-11.

Ответ:-11

(-2;4)

k=

(2;3)

(-4;1)

(-1;0)

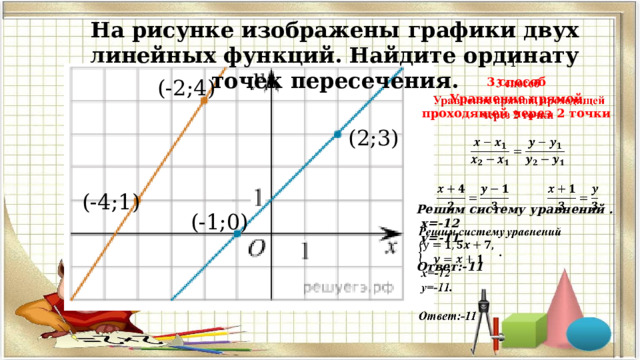
На рисунке изображены графики двух линейных функций. Найдите ординату точек пересечения.

1

(-2;4)

3 способ

Уравнение прямой, проходящей через 2 точки

Решим систему уравнений .

х=-12

у=-11.

Ответ:-11

(2;3)

(-4;1)

(-1;0)

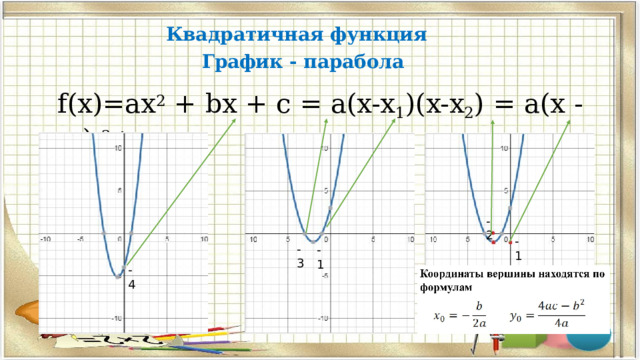
Квадратичная функция График - парабола

f(x)=ax 2 + bx + c = a(x-x 1 )(x-x 2 ) = a(x - m) 2 + n

-2

-1

-3

-1

-4

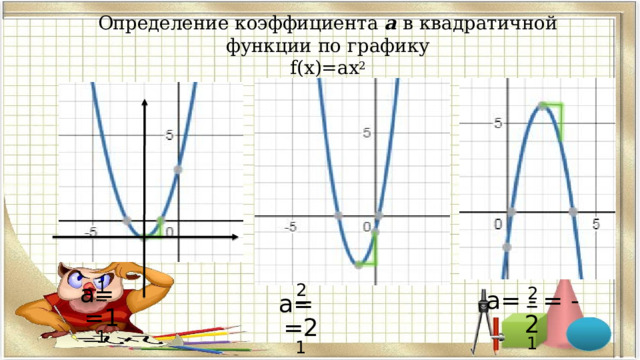
Определение коэффициента а в квадратичной функции по графику f(x)=ax 2

1

2

2

a= =1

1

a= - = -2

1

a= =2

1

На рисунке изображен график функции f(x)= x²+bx+c ,

где числа a,b и c -целые. Найдите значение f(-12).

Решение.

f(x)= (x-m)²+n,где m, n-координаты вершины параболы.

m= -4,n= -3, =1.

f(x)=(x-(-4))²+(-3),

f(x)=(x+4)²-3,

f(-12)=(-12+4)²-3,

f(-12)=61.

Ответ:61

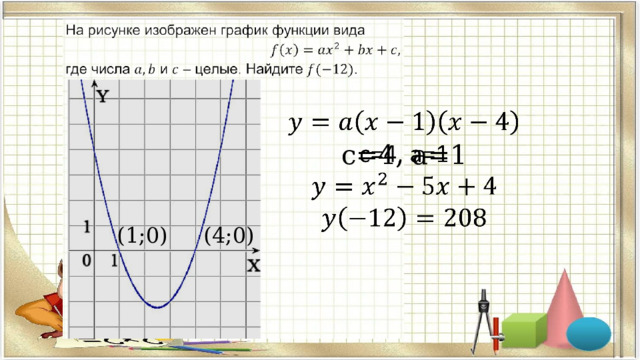
с=4, а=1

(1;0)

(4;0)

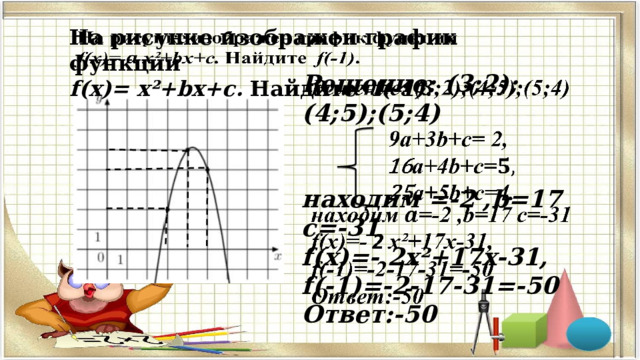
На рисунке изображен график функции

f(x)= x²+bx+c. Найдите f(-1) .

Решение: (3;2);(4;5);(5;4)

находим =-2 ,b=17 с=-31

f(x)=- 2 x²+17x-31,

f(-1)=-2-17-31=-50

Ответ:-50

На рисунке изображен график функции f(x)=ах ² +bx+c ,где числа ,b и c -целые. Найдите абсциссу вершины параболы.

Решение.

Абсцисса вершины параболы найдем по формуле = -

Из рисунка видно, что f(-3)=-2; f(-2)=1; f(-1)=6.Тогда

вычтем из 1 уравнения 2-е, получим5a-b=-

вычтем из 2 уравнения 3-е,получим 3a-b=-

Решив систему уравненийнаходим =1 ,b=8.

Абсцисса вершины параболы = - =-4.

Ответ:-4

На рисунке изображены графики функций f(x)=5х+9 и g(x)= ах ² +bx+c, которые пересекаются в точках А и В. Найдите абсциссу точки B

Решение. По графику с=-3.График функции g(x) проходит через точки (-2;-1);(-1;-3);(2;3).

Подставим координаты точки (-1;-3), получим

-3=а- b-3.Отсюда а=b.

g(x)= ах ² +аx-3.

Подставим координаты точки (2;3), получим, что а=1.

g(x)= х ² +x-3.

Чтобы найти абсциссу точки ,нужно решить уравнение х ² +x-3=5х+9,

х ² -4x-12=0.

По теореме Виета =-12, +=4

По графику =-2, тогда=6.

Ответ:6

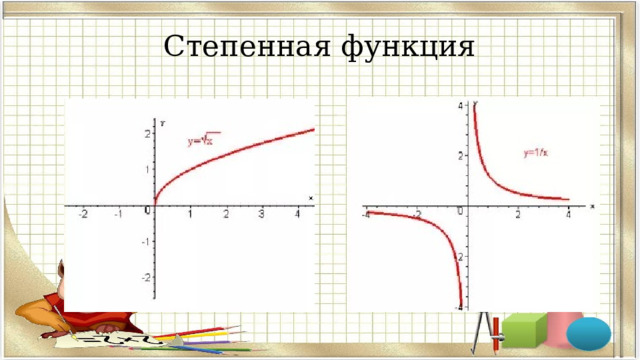
Степенная функция

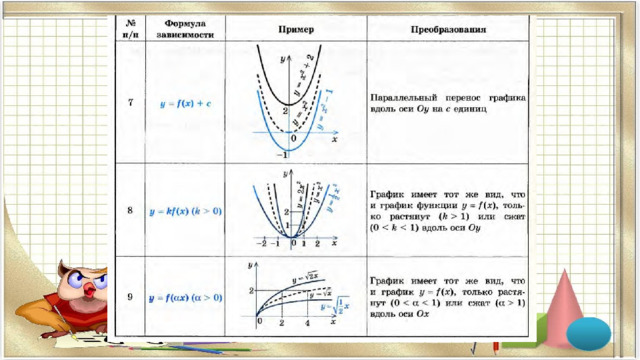
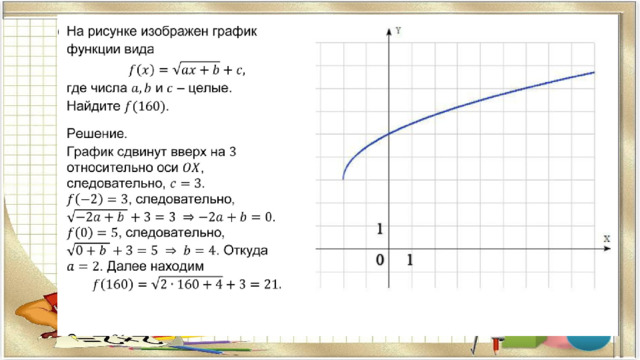
Другой способ решения

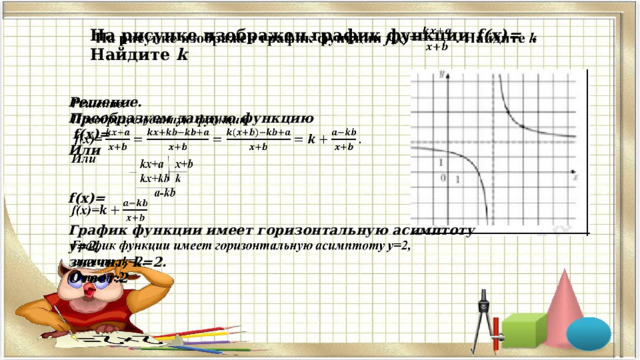
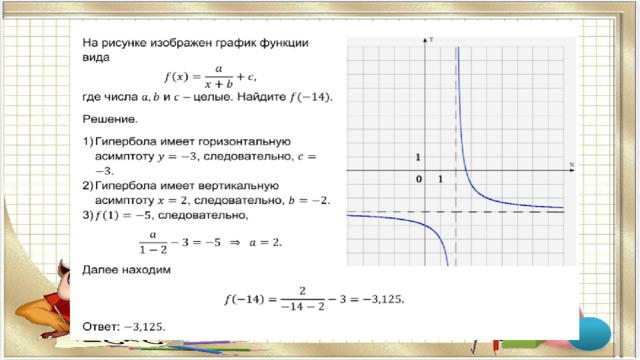
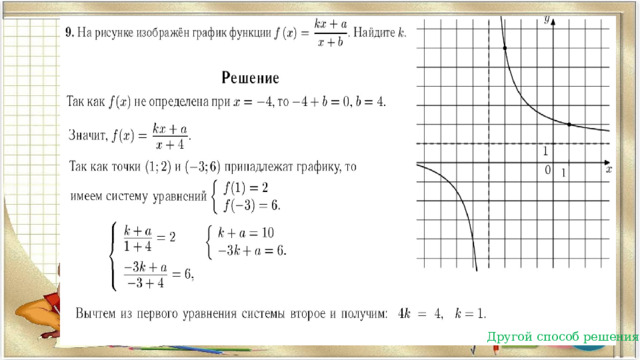
На рисунке изображен график функции f(x)= . Найдите k

Решение.

Преобразуем данную функцию

f(x)=

Или

f(x)=

График функции имеет горизонтальную асимптоту y=2,

значит, k=2.

Ответ:2

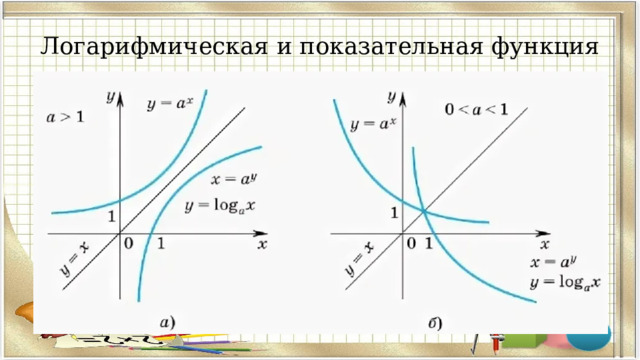
Логарифмическая и показательная функция

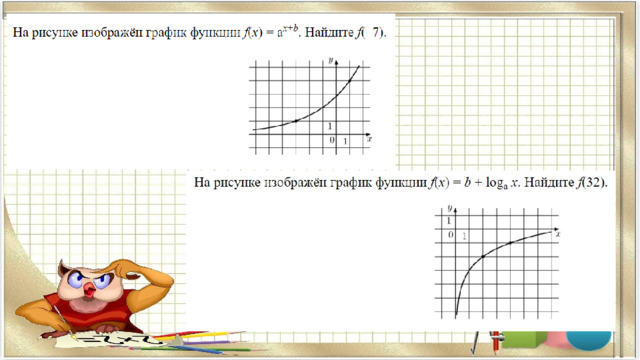
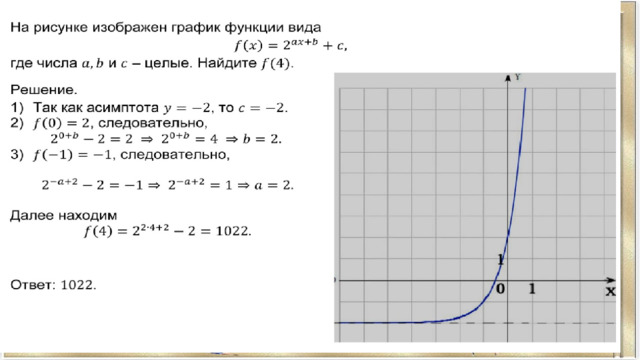
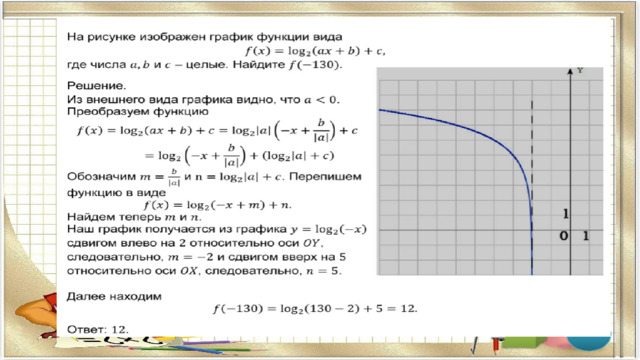
Кусочная функция

Тригонометрические функции

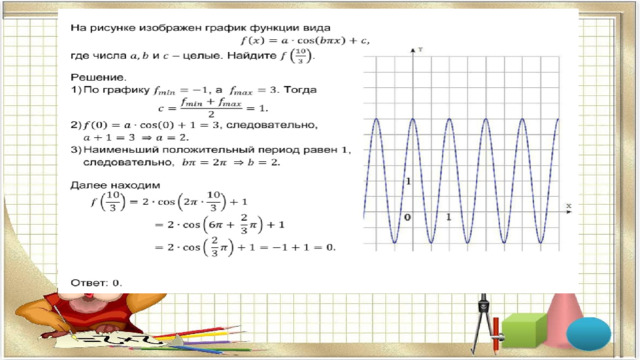
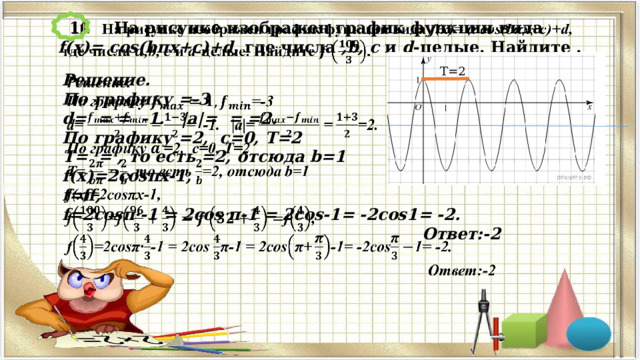
11 На рисунке изображен график функции вида f(x)= cos(bπx+c)+d, где числа ,b, c и d -целые. Найдите .

Т=2

Решение.

По графику =-3

d= = = -1. |a|= = =2.

По графику =2, c=0, T=2

T= = , то есть =2, отсюда b=1

f(x)=2cosπx-1,

f=ff,

f=2cosπ·-1 = 2cos π-1 = 2cos-1= -2cos1= -2.

Ответ:-2

Ссылки для задания №11

• ✅Все НОВЫЕ Задания №11 ЕГЭ 2024 Профиль с сайта.. | ege314.ru | ОГЭ и ЕГЭ по математике 2024 (vk.com )
• Задачи 11 ЕГЭ профильная математика, сортировка по темам (mathm.ru )
• 9. Функции и их свойства (ege314.ru )
• Новое ЕГЭ по математике — Профиль 2024. Открытый банк заданий с ответами. — math100.ru
• Задание 11 ЕГЭ по математике. Графики функций (ege-study.ru)