Алгоритмические структуры

В математике для решения типовых задач мы используем определенные правила, описывающие последовательности действий. Например, правила сложения дробных чисел, решения квадратных уравнений и т. д. Обычно любые инструкции и правила представляют собой последовательность действий, которые необходимо выполнить в определенном порядке. Для решения задачи надо знать, что дано, что следует получить и какие действия и в каком порядке следует для этого выполнить.

Предписание, определяющее порядок выполнения действий над данными с целью получения искомых результатов, и есть алгоритм.

В презентации из 22 слайдов демонстрируется:

- тема и содержание урока;

- что такое алгоритм и его свойства;

- форма записи алгоритма;

- приводятся примеры задач.

Методическая разработка урока по теме: «Алгоритмические структуры»

Козлова Татьяна Сергеевна

учитель математики и информатики

МОУ «СОШ № 42» г. Воркуты

Разгадайте тему урока, выполнив задания на карточках

А

Л

11010110000

Г

1530

О

358

Р

0,0101

И

0,24

Т

0,5

М

101000,01

Ы

50,2

28,4

Далее

Алгоритмы

Содержание

• Что такое алгоритм?
• Свойства алгоритма.
• Форма записи алгоритмов.
• Базовые алгоритмические структуры.
• Решение задачи на языке блок-схем

Что такое алгоритм?

В математике для решения типовых задач мы используем определенные правила, описывающие последовательности действий. Например, правила сложения дробных чисел, решения квадратных уравнений и т. д. Обычно любые инструкции и правила представляют собой последовательность действий, которые необходимо выполнить в определенном порядке. Для решения задачи надо знать, что дано, что следует получить и какие действия и в каком порядке следует для этого выполнить. Предписание, определяющее порядок выполнения действий над данными с целью получения искомых результатов, и есть алгоритм.

Далее

Алгоpитм — заранее заданное понятное и точное предписание возможному исполнителю совершить определенную последовательность действий для получения решения задачи за конечное число шагов.

Название "алгоритм" произошло от имени среднеазиатского математика Мухаммеда ибн Муса аль-Хорезми (Alhorithmi), (783—850 гг). В книге "Об индийском счете" он изложил правила записи натуральных чисел с помощью арабских цифр и правила действий над ними "столбиком", знакомые теперь каждому школьнику. С наступлением эры информатики алгоритмы становятся одним из важнейших факторов цивилизации.

Назад

Свойства алгоритма

Основные свойства алгоритмов следующие:

1. Понятность для исполнителя — исполнитель алгоритма должен понимать, как его выполнять. Иными словами, имея алгоритм и произвольный вариант исходных данных, исполнитель должен знать, как надо действовать для выполнения этого алгоритма.

2. Дискpетность (прерывность, раздельность) — алгоpитм должен пpедставлять пpоцесс pешения задачи как последовательное выполнение пpостых (или pанее опpеделенных) шагов (этапов).

3.Опpеделенность — каждое пpавило алгоpитма должно быть четким, однозначным и не оставлять места для пpоизвола. Благодаpя этому свойству выполнение алгоpитма носит механический хаpактеp и не тpебует никаких дополнительных указаний или сведений о pешаемой задаче.

Далее

4. Pезультативность (или конечность) состоит в том, что за конечное число шагов алгоpитм либо должен пpиводить к pешению задачи, либо после конечного числа шагов останавливаться из-за невозможности получить решение с выдачей соответствующего сообщения, либо неограниченно продолжаться в течение времени, отведенного для исполнения алгоритма, с выдачей промежуточных результатов.

5. Массовость означает, что алгоpитм pешения задачи pазpабатывается в общем виде, т.е. он должен быть пpименим для некотоpого класса задач, pазличающихся лишь исходными данными. Пpи этом исходные данные могут выбиpаться из некотоpой области, котоpая называется областью пpименимости алгоpитма.

Назад

Форма записи алгоритма.

На практике наиболее распространены следующие формы представления алгоритмов:

• словесная (запись на естественном языке);
• графическая (изображения из графических символов);
• алгоритмический язык (полуформализованные описания алгоритмов на условном алгоритмическом языке, включающие в себя как элементы языка программирования, так и фразы естественного языка, общепринятые математические обозначения и др.);
• программная (тексты на языках программирования).

Далее

Словесное описание алгоритма.

Словесный способ записи алгоритмов представляет собой описание последовательных этапов обработки данных. Алгоритм задается в произвольном изложении на естественном языке

Словесный способ не имеет широкого распространения, так как такие описания:

• строго не формализуемы; страдают многословностью записей;
• допускают неоднозначность толкования отдельных предписаний.

Далее

Назад

Например. Записать алгоритм сложения или вычитания десятичных дробей в «столбик»

Вместе формулируем алгоритм:

1 ) Уравнять в дробях количество знаков после запятой;

2) Записать их «в столбик» так, чтобы запятая оказалась под запятой;

3) Выполнить сложение (вычитание),не обращая внимания на запятую;

4) Поставить запятую под запятой.

Назад

Далее

Графическое описание алгоритма.

При графическом представлении алгоритм изображается в виде последовательности связанных между собой функциональных блоков, каждый из которых соответствует выполнению одного или нескольких действий.

Такое графическое представление называется схемой алгоритма или блок-схемой. В блок-схеме каждому типу действий (вводу исходных данных, вычислению значений выражений, проверке условий, управлению повторением действий, окончанию обработки и т.п.) соответствует геометрическая фигура, представленная в виде блочного символа. Блочные символы соединяются линиями переходов, определяющими очередность выполнения действий. В таблице приведены наиболее часто употребляемые символы.  

Назад

Далее

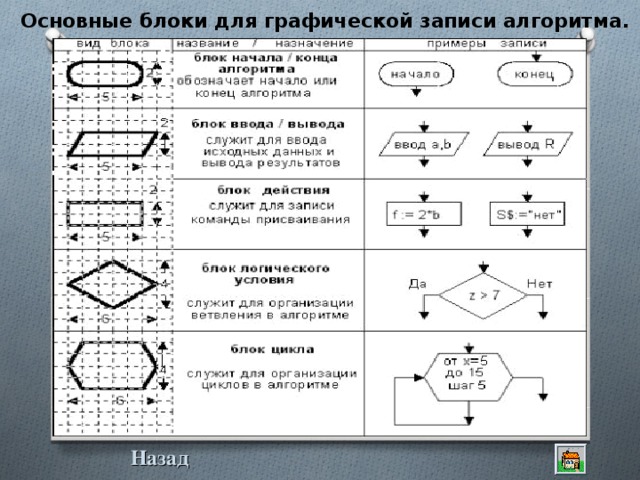
Основные блоки для графической записи алгоритма.

Назад

Базовые алгоритмические структуры.

Выделяют следующие виды алгоритмов: линейный, разветвляющийся, циклический и комбинированный. При определении вида алгоритма пользуются ключевыми словами.

Вид алгоритма.

Ключевые слова

Алгоритм, в котором есть структура СЛЕДОВАНИЕ называется линейным.

Следование – расположение действий друг за другом

Структура

Ключевых слов нет.

Далее

Алгоритм, в котором есть структура ВЕТВЛЕНИЕ называется разветвляющимся. Ветвление – выбор действия от какого-либо условия.

Если…то…иначе…;

При…(в значении если)

If Условие Then Серия 1 Else Серия 2 End If

При выборе нескольких условий используют оператор Case

Алгоритм, в котором есть структура ЦИКЛ называется циклическим.

Цикл – неоднократное повторение каких-либо действий.

Do While Тело Цикла Loop Условие

От…до…; …раз;

Пока…;

Если…(в значении пока…);

For Счетчик=НачЗнач To КонЗнач [ Step шаг ] Тело цикла Next

Do While Условие Тело Цикла Loop

Do Until Условие Тело Цикла Loop

Далее

Примеры алгоритмов

Линейный

Ветвление

Циклический

Назад

Далее

Линейный алгоритм.

На рисунке представлен алгоритм

лепки снеговика.

Назад

Далее

Ветвление

На рисунке

продемонстрирован

алгоритм ветвления

на примере выбора

пути маршрута.

Назад

Далее

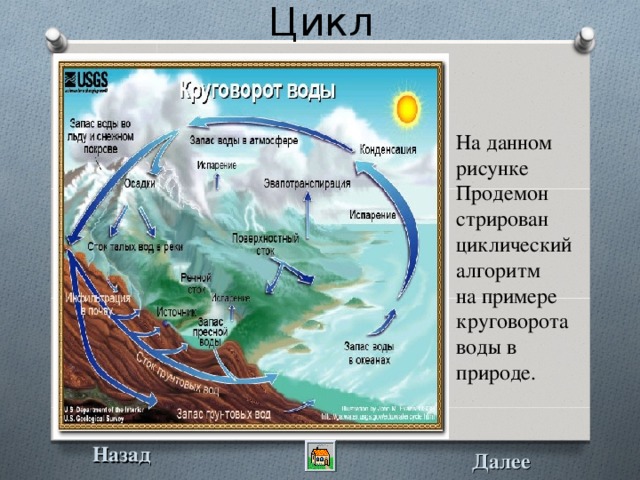
Цикл

На данном рисунке

Продемон

стрирован

циклический алгоритм

на примере круговорота

воды в природе.

Назад

Далее

Описание на псевдокодах

Далее

Описание на языке программирования

Нахождение площади треугольника по двум сторонам и углу между ними

Решение:

Program ploshad;

var a,b,s,u:real;

BEGIN

writeln('Ввести длины сторон треугольника');

readln(a,b);

writeln('Ввести величину угла между ними');

readln(u);

S:=1/2*a*b*sin(u);

writeln('Площадь равна',S);

END.

Далее

Решите задачу на языке блок-схем

ПРИМЕР 1.1. Зная длины трех сторон треугольника, вычислить площадь и периметр треугольника.

Пусть a, b, c - длины сторон треугольника. Необходимо найти S - площадь треугольника, P - периметр. Для нахождения площади можно воспользоваться формулой Герона: где r - полупериметр.

Входные данные: a, b, c.

Выходные данные: S, P.