Алгоритмы решения задач стереометрии в системе GAP

Алгоритмы решения задач стереометрии в системе GAP

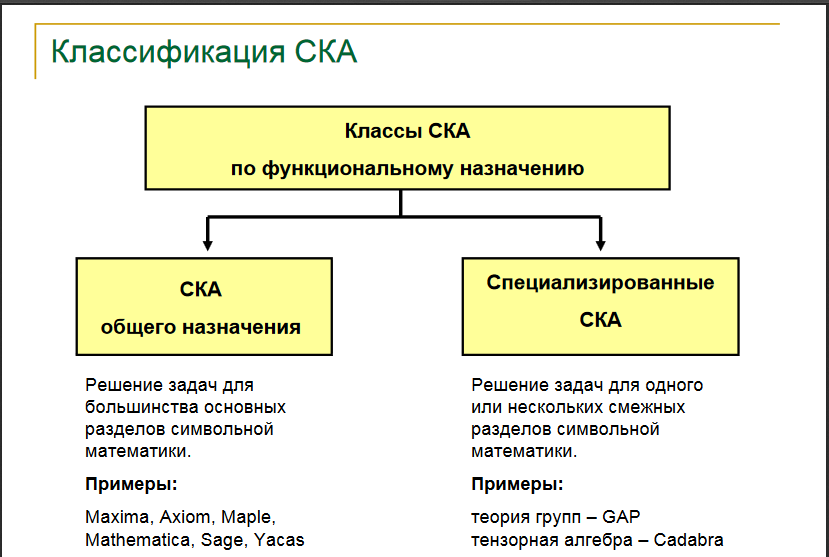
GAP - свободно распространяемая, открытая и расширяемая система компьютерной алгебры, название которой означает "Groups, Algorithms and Programming". Является системой компьютерной алгебры, задуманной как инструмент вычислительной теории групп, и впоследствии распространившейся на смежные разделы алгебры. В настоящее время GAP является уникальным всемирным совместным научным проектом, объединяющим специалистов в области алгебры, теории чисел, математической логики, информатики и др. наук из различных стран мира. Разработка системы была начата в 1986 г. Первоначально GAP разрабатывался в г. Аахен, Германия (Lehrstuhl D fur Mathematik, RWTH). В настоящее время центр разработки GAP и технической поддержки его пользователей находится в Шотландии (School of Mathematical and Computational Sciences, University of St.-Andrews).

• язык программирования, внешне напоминающий Паскаль;

• стандартные типы основных алгебраических объектов: групп (под- становок, абстрактных, матричных), колец, полей;

• удобные типы переменных, в т.ч. оперативно изменяемые списки и записи;

• более 4 тысяч библиотечных функций;

• обширная библиотека данных, включая практически все группы, по- рядок которых не превосходит 1000;

• прикладные программы, поставляемые вместе с GAP, охватывают такие разделы алгебры, как комбинаторная теория групп, конечные простые группы, теория представлений групп, теория графов, в т.ч. их группы автоморфизмов, теория кодирования, кристаллографиче- ские группы, группы Галуа и многое другое;

• подробное и удобное описание (около 1600 стр.) в формате «гипертекст»;

• бесплатное получение по сети Internet вместе с исходными текстами, являющимися незаменимым наглядным пособием для освоения GAP;

• работа в операционных системах DOS, Windows, Unix, Linux, MacOS;

• работа с процессором типа 386 и выше с ОЗУ от 8 Mb;

• занимаемое место на диске - от 10 до 100 Mb в зависимости от объема инсталляции;

• способность работать с ОЗУ до 128 Mb и файлом подкачки до 128 Mb.

GAP дает возможность производить вычисления с гигантскими целыми и рациональными числами, допустимые значения которых ограничены только объемом доступной памяти. Далее, система работает с конечными полями, мно- гочленами от многих переменных, рациональными функциями, векторами и мат- рицами. Пользователю доступны различные комбинаторные функции, элемен- тарные теоретико-числовые функции, разнообразные функции для работы с мно- жествами и списками.

Группы могут быть заданы в различной форме, например, как группы под- становок, матричные группы, группы, заданные порождающими элементами и определяющими соотношениями. Более того, построив, например, групповую алгебру, можно вычислить ее мультипликативную группу, и даже задать ее под- группу, порожденную конкретными обратимыми элементами групповой ал- гебры. Ряд групп может быть задан непосредственным обращением к библиотеч- ным функциям (например, симметрическая и знакопеременная группы, группа диэдра, циклическая группа и др.).

Функции для работы с группами включают определение порядка группы, вычисление классов сопряженных элементов, центра и коммутанта группы,

верхнего и нижнего центрального рядов, ряда коммутантов, Силовских под- групп, максимальных подгрупп, нормальных подгрупп, решеток подгрупп, групп автоморфизмов, и т.д. Для ряда конечных групп доступно определение их типа изоморфизма.

Теория представлений групп также входит в область применения си- стемы GAP. Здесь имеются инструменты для вычисления таблиц характеров кон- кретных групп, действий над характерами и интерактивного построения таблиц характеров, определения теоретико-групповых свойств на основании свойств таблицы характеров группы. Модулярные представления групп (т.е. представле- ния над полем, характеристика которого делит порядок группы) также могут быть исследованы с помощью GAP.

В версии 4.3, в которой были производены вычисления, были существен- ным образом расширены возможности для работы с векторными простран- ствами, алгебрами и модулями. В системе могут быть определены векторные пространства над всеми доступными полями и модули над всеми доступными кольцами. Имеются алгоритмы для вычисления структуры конечномерных ал- гебр Ли, которые могут быть, например, заданы структурными константами или порождающими элементами, вычисления различных их Лиевских подалгебр и идеалов.

Ключевыми словами GAP являются следующие слова: and, do, elif, else, end, fi, for, function, if, in, local, mod, not, od, or, repeat, return, then, until, while, quit, QUIT, break, rec, continue.

Примерами выражений являются: переменные, обращения к функциям, це- лые числа, перестановки, строки, функции, списки, записи. С помощью операто- ров из них могут быть составлены более сложные выражения. Операторы раз- биты на три класса:

• операторы сравнения: =, , , =, in;

• арифметические операторы: +, -, *, /, mod, ^;

• логические операторы: not, and, or.

gap2*2;; #два знака ";" подавляют вывод на экран gap2*2+9=Fibonacci(7) and Fibonacci(13) in Prime; true

Формат:

left-expr = right-expr left-exprright-expr

Примечание: любые объекты сравнимы между собой. Объекты различных типов всегда различны, т.е. = приведет к false, и — к true. Кроме того, для них определено отношение «меньше».

Операторы сравнения имеют больший приоритет по сравнению с логиче- скими операторами, но меньший по сравнению с арифметическими. Например, a*b = c and d интерпретируется как ((a*b)=c) and d). Еще один пример (сравнение, левая часть которого является выражением ):

gap 2 * 2 + 9 = Fibonacci(7); true

Формат:

+ right-expr

- right-expr

eft-expr + right-expr

left-expr - right-expr left-expr * right-expr eft-expr / right-expr

left-expr mod right-expr left-expr ^ right-expr

Значение, как правило, зависит от типа операндов. Mod определен только для целых и рациональных чисел. Для элемента группы ^ означает возведение в степень, если правый операнд - целое число, а если он — также элемент группы, то сопряжение с его помощью. Приоритет операторов (по убыванию):

3) ^

1. унарные + и - 5) *, /, mod

6) + и -

Пример: -2 ^ -2 * 3 + 1 означает (-(2 ^ (-2)) * 3) + 1 .

Арифметические операторы имеют наивысший приоритет по сравнению с операторами сравнения и логическими операторами.

Присваивания имеют формат var := expr;

Формат: procedure-var();

procedure-var(arg-expr {, arg-expr} );

Различие между процедурами и функциями введено для удобства, GAP же их не различает. Функция возвращает значение, но не производит побочных эф- фектов. Процедура не возвращает никакого значения, но производит какое-либо действие (например, процедуры Print, Append, Sort).

Формат:

if bool-expr1 then statements1

{ elif bool-expr2 then statements2 } [ else statements3 ]

fi;

При этом частей elif может быть произвольное количество или ни одной.

Часть else также может отсутствовать.

Формат:

function ( [ arg-ident {, arg-ident} ] ) [ localloc-ident {, loc-ident} ; ]

Математические модели, как планиметрии, так и стереометрии, основаны на векторной алгебре, хотя и не используют явно понятие векторного пространства. Наглядность изложения векторной алгебры и ее приложений к стереометрии играет первоочередную роль. Системы компьютерной математики (СКМ), особенно Maple, обладающие уникальными графическими возможностями, способны в полной мере продемонстрировать эту наглядность.

Процесс компьютерного моделирования фигур и объектов аналитической геометрии состоит из трех этапов: на первом этапе в координатном представлении вычисляются результаты вектор- ных операций; на втором этапе конструируются графические объекты, соответствующие этим операциям, наконец, на заключительном, третьем этапе, производится сборка сложных графических структур на основе простых. Сборка осуществляется с помощью команды display библиотеки Maple plots. Таким образом, можно сконструировать достаточно сложные многопараметрические программные процедуры, позволяющие контролировать свойства конструируемых графических объектов. Такие процедуры удобно объединить в пользовательскую библиотеку про- граммных процедур.

Алгоритмы, которые могут использоваться к решению задач в стереометрии, компьютерное моделирование объектов стереометрии:

На третьем этапе компьютерного моделирования конструируются программные процедуры изображения геометрических фигур. Продемонстрируем пример создания

процедуры Nagle(R,a,n,c) графического отображения призмы с ребром a (список), окрашенной в цвет c, в основании которой лежит правильный n-угольник, вписанный в окружность радиуса R:

VectorAlgebra[Nagle]:=proc(R,a,n,c) local

M,i,MN,Ma,MNa,ab,t,k,gab:

M:=(i)-[R*cos(2*Pi*i/n),R*sin(2*Pi*i/n),0]:

Ma:=(i)-[R*cos(2*Pi*i/n)+a[1],

R*sin(2*Pi*i/n)+a[2],a[3]]:

MN:=plots[polygonplot3d]([seq(Ma(i),i=1..n)],style

=WIREFRAME,color=c):MNa:=plots[polygon-

plot3d]([seq(M(i),i=1..n)]

,style=WIREFRAME,color=c):

ab:=(i,t)-[seq(M(i)[k]+a[k]*t,k=1..3)]:

gab:=(i)-

plots[spacecurve](ab(i,t),t=0..1,color=c):

plots[display](MN,MNa,seq(gab(i),i=1..n)):end

proc:

Результат исполнения этой процедуры показан на Рис.1:

VectorAlgebra[Nagle]:=proc(R,a,n,c)

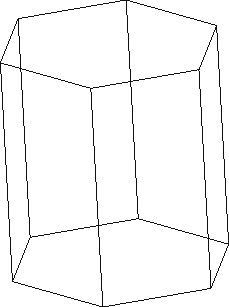
Рис.1. Графическая иллюстрация призмы VectorAlge- bra[Nagle](2,[1,2,3],5,red);

Пользовательская библиотека программных процедур "Vector-Algebra" содержит следующие процедуры:

• Reper(A,a,b,c,g,c1,c2,c3) – процедура графической иллюстрации координатного репера с опорной точкой A, и базисными векторами a,b,c, где g=n ´ m – количество отображаемых линий координатной сети, c1,c2,c3 – цвета соот- ветствующих плоскостей.

• Reper_name(A,a,b,c,g,c1,c2,c3,p,t,r,d) – процедура графического изображения подписей к координатным осям репера, где a,b,c – базис- ные векторы, g=n ´ m – количество отображаемых линий координатной сети, c1,c2,c3 – цвета соответствующих плоскостей, p,t,r – подписи к осям, d – цвет надписей на осях координат.

• Reper_pr (A,a,b,c,g,x1,y1,z1,x2,y2,z2,c1,c2, c3,c4,c5,p,t,r,d) – процедура графического изображения вектора с его проекциями в трехмер- ной системе координат. Эта процедура является комплексной, содержащей все выше перечисленные процедуры, вложенные друг в друга; здесь a,b,c – координаты заданных векторов, x1,y1,z1 – координаты начала вектора, x2,y2,z2 – координаты конца вектора, c1,c2,c3 – цвета соответствующих плоскостей, c4 – цвет изображения вектора, c5 – цвет его проекции на координатные плоскости, d – цвет надписей на осях координат.

• parallelogram(A,a,b) – процедура гра- фической иллюстрации параллелограмма где a, b, заданные векторы, приложенные к точке A.

• paralleiepiped_ABCD](A,a,b,c) и pyramid_ABCDE](A,a,b,c) – аналогичные процедуры визуализации параллелепипеда и тетраэдра.

На рис.2, 3 и 4 показано исполнение процедур S_vec(A,a,b),Prod_ vec(A,a,b) и Vec_Pr(M,x,e):

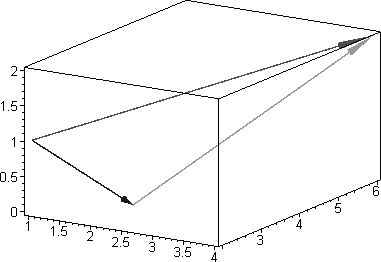
Рис.2. Исполнение графической иллюстрации сложе- ния векторов S_vec ([1,2,1],[1,1,1],[2,3,2]);

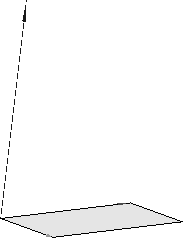
Рис.3. Исполнение процедуры векторного произведения Prod_vec ([1,2,1], [1,1,-1],[2,3,2]);

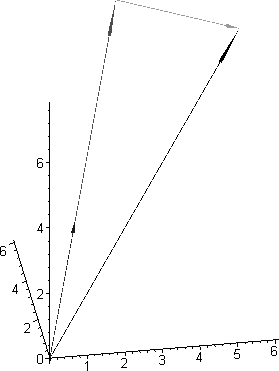
Рис.4. Исполнение графической иллюстрации параллельной и перпендикулярной составляющих вектора Vec_Pr([0,0,0],[10,10,10],[2,4,3])