ФГБОУ ВО «МОРДОВСКИЙ ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ ИНСТИТУТ ИМЕНИ М. Е. ЕВСЕВЬЕВА»
Факультет физико-математический
Реферат
на тему: Алгоритмы
построения поверхностей по аналитическому уравнению
Реферат выполнил
студент 5 курса группы МДМ-112______________М. С. Муратова
Реферат проверила ______________________Т. В. Кормилицына
Саранск 2017
Поверхностью второго порядка называется геометрическая фигура, которая в некоторой декартовой системе координат описывается уравнением
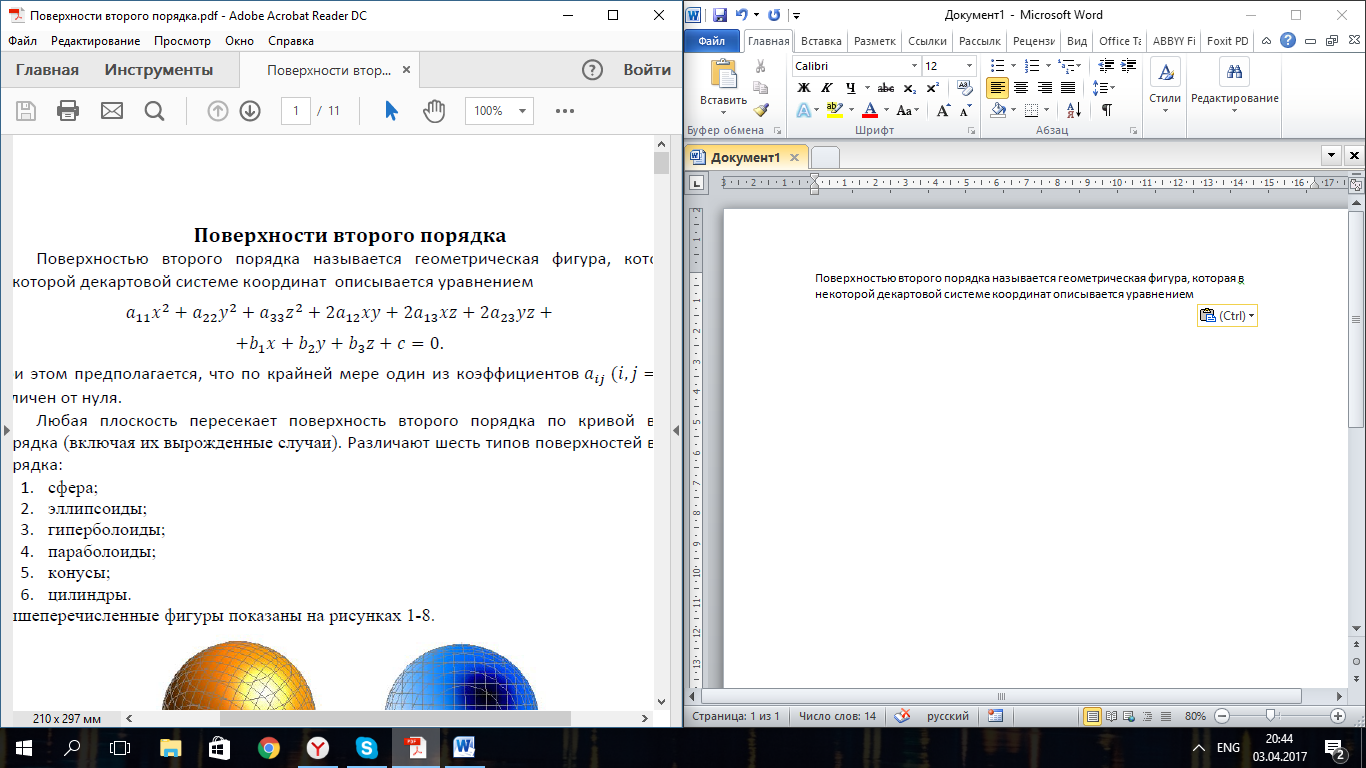
При этом предполагается, что по крайней мере один из коэффициентов отличен от нуля.
Любая плоскость пересекает поверхность второго порядка по кривой второго порядка (включая их вырожденные случаи). Различают шесть типов поверхностей второго порядка:
1. сфера;
2. эллипсоиды;
3. гиперболоиды;
4. параболоиды;
5. конусы;
6. цилиндры.
Сфера
Сфера представляет собой геометрическое место точек пространства, равноудалённых от некоторой точки, называемой центром сферы. В декартовой системе координат сфера описывается уравнением
![]()
Где 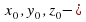 координаты центра сферы; R – радиус сферы.
координаты центра сферы; R – радиус сферы.
Сфера является телом, образованным вращением полуокружности вокруг своего диаметра.
Если центр сферы расположен в начале декартовой системы координат, то уравнение этой поверхности имеет вид
![]()
и называется каноническим уравнением сферы, а соответствующая система координат называется канонической.
Эллипсоиды
Эллипсоидом называется поверхность, которая в некоторой декартовой системе координат описывается уравнением
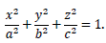
Это равенство называется каноническим уравнением эллипсоида. Величины a,b и c называются полуосями эллипсоида.
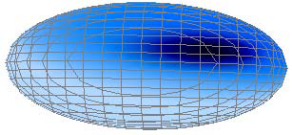
Эллипсоид может быть получен равномерным сжатием или растяжением сферы вдоль трёх взаимно перпендикулярных осей. Говоря иначе, уравнение эллипсоида получается из уравнения сферы масштабным преобразованием ![]()
Если какие‐либо две оси эллипсоида одинаковы, то эллипсоид называют сфероидом.
В этом случае эллипсоид является телом, образованным вращением половины дуги эллипса вокруг оси, соединяющей концы этой дуги. Пусть, например, 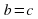 . Тогда эллипсоид
. Тогда эллипсоид
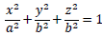
образован вращением верхней половины дуги эллипса, вокруг оси 0x.
Гиперболоиды
Гиперболоидом называется поверхность, которая в некоторой декартовой системе координат описывается одним из уравнений:
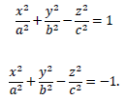
Величины a,b,c называются полуосями гиперболоида.
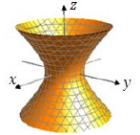
Однополостный гиперболоид ![]() .
.
Двухполостный гиперболоид ![]() .
.
Отметим, что
• однополостный гиперболоид вращения может быть получен вращением прямой вокруг некоторой скрещивающейся с ней прямой;
• двухполостный гиперболоид вращения является геометрическим местом точек, модуль разности расстояний от которых до двух заданных точек, называемых фокусами гиперболоида, есть величина постоянная.
Параболоиды
Параболоидом называется поверхность, которая в некоторой декартовой системе координат описывается одним из уравнений:
![]()
![]()
Параболоид представляет собой незамкнутую нецентральную поверхность (не имеющую центра симметрии).

Если p=q, то параболоид называется круговым и является телом вращения, образованным вращением одной ветви параболы 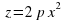 вокруг оси Oz.
вокруг оси Oz.
Если один из коэффициентов p или q равен нулю, то параболоид называется цилиндрическим.
Конусы
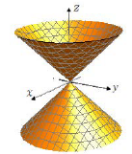
Каноническое уравнение конуса второго порядка можно представить в виде
![]()
В этом случае точка O(0,0,0) является вершиной конуса, а ось 0z – осью конуса.
Цилиндры
Если направляющая цилиндрической поверхности задается кривой второго порядка, то такая поверхность называется цилиндрической поверхностью второго порядка.
Эллиптической цилиндр: 
Параболический цилиндр: 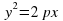
Гиперболический цилиндр: 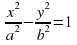

 Получите свидетельство
Получите свидетельство Вход
Вход












 Алгоритмы построения поверхностей по аналитическому уравнению (594.95 KB)
Алгоритмы построения поверхностей по аналитическому уравнению (594.95 KB)
 0
0 226
226 7
7 Нравится
0
Нравится
0


