3D построение в Scilab

ФГБОУ ВО «МОРДОВСКИЙ ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ ИНСТИТУТ ИМЕНИ М.Е.ЕВСЕВЬЕВА»

Факультет физико-математический

Кафедра информатики и вычислительной техники

РЕФЕРАТ

3D построение в Scilab

Выполнила: К. В. Василькина, студентка 5 курса, гр. МДМ-112

Направление подготовки 44.03.05 Педагогическое образование.

Профиль Математика. Информатика

Проверила: Т. В. Кормилицына, канд. физ-мат. н., доцент

Саранск 2017

Содержание

1. Что такое Scilab?............................................................................3

2. Возможности Scilab для построения поверхностей………………5

3. Построение графиков поверхностей, заданных параметрически.10

4. Построение трехмерной линии, заданной параметрически…….12

Список использованной литературы……………………………………12

1. Что такое Scilab?

Scilab - пакет прикладных математических программ, предоставляющий открытое окружение для инженерных (технических) и научных расчётов.

Scilab был спроектирован как открытая система, и пользователи могут добавлять в него свои типы данных и операции путём перегрузки.

Хотя первоначальный акцент при разработке пакета был сделан на матричную алгебру, вскоре функциональные возможности расширились настолько, что охватили большинство разделов научных вычислений, включая:

• 2D и 3D графики, анимацию;

• линейную алгебру и матрицы;

• полиномы и рациональные функции;

• интерполяцию и аппроксимацию;

• линейную, квадратичную и нелинейную оптимизацию;

• обыкновенные дифференциальные уравнения, дифференциально-алгебраические уравнения;

• решение линейных матричных неравенств;

• оптимизацию дифференцируемых и не дифференцируемых функций;

• обработку сигналов;

• математическую статистику.

Программа доступна для различных операционных систем, включая Linux, Microsoft Windows и Mac OS X. Возможности Scilab могут быть расширены внешними программами и модулями, написанными на разных языках программирования. Отличие от других программ заключается в том, что Scilab находится в свободном доступе, бесплатный.

Логотип Scilab:

Интерфейс: На рисунке показан интерфейс программы, начиная с версии 5.5.

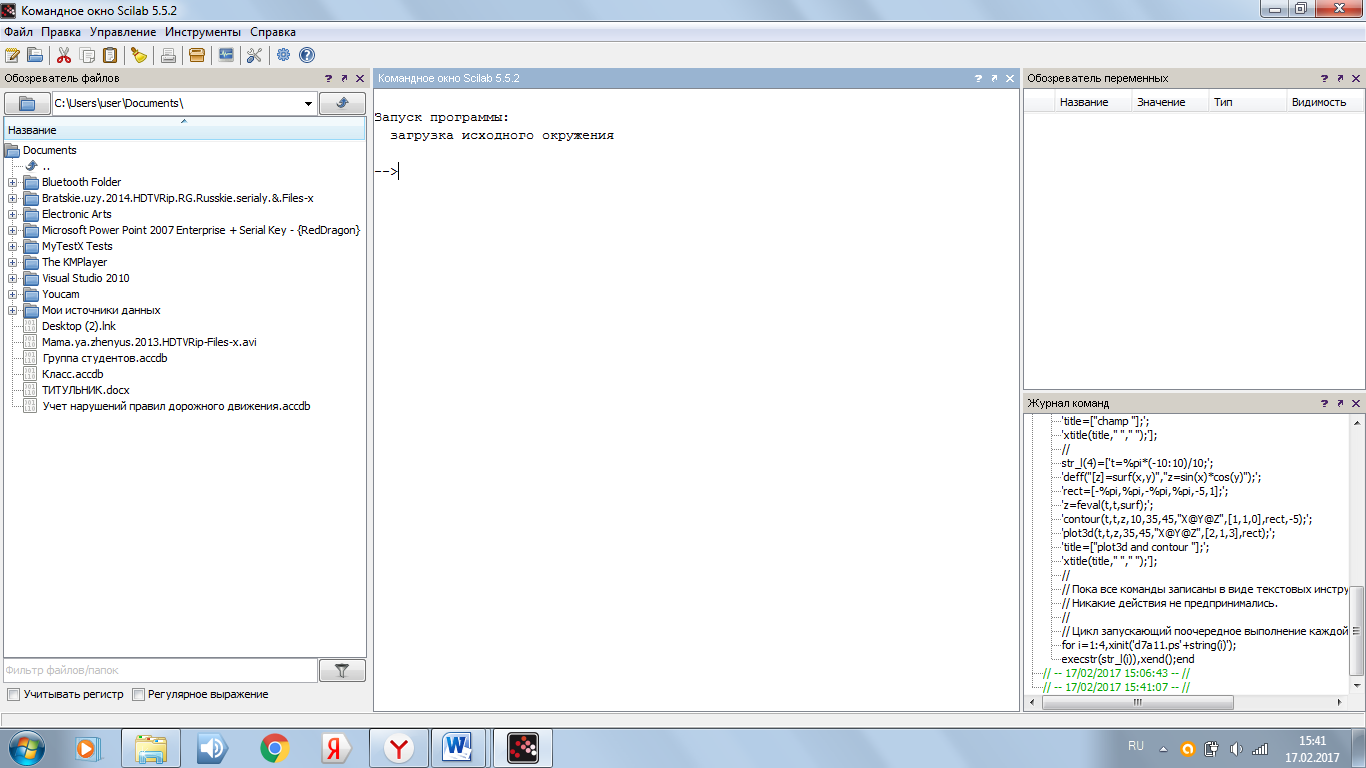
• Обозреватель файлов;

• Командное окно;

• Обозреватель переменных;

• Журнал команд.

Приведём простейшие вычисления в Scilab.

1. Вычислить площадь круга и длину окружности радиуса r=5.78.

Решение:

Площадь круга и длина окружности вычисляются по формулам:

S=∗r, l=2∗r соответственно, где r — радиус круга/окружности. Вычислим площадь круга и длину окружности радиуса r=5.78 .

--S=%pi*5.78^2

S =

104.95558

1. Код, задающий матрицу и считающий определитель:

M=[1 6 8; 7 8 8; 1 6 0]

det(M)

1. Возможности Scilab для построения поверхностей

В Scilab поверхность можно построить с помощью функций plot3d или plot3d1. Их отличие состоит в том что, plot3d строит поверхность и заливает ее одним цветом, а plot3d1 поверхность, каждая ячейка которой имеет цвет, зависящий от значения функции в каждом, соответствующем узле сетки (см рис. 2).

Рисунок 2. Отличие функций plot3d и plot3d

В функциях plot3d(x,y,z), plot3d1(x,y,z) три переменные, x – вектор-столбец значений абсцисс; y – вектор-столбец значений ординат; z – матрица значений функции в узлах сетки.

Задача 1. Построить график функции Z=sin(t)⋅cos(t) при помощи команды plot3d (см. рис. 3).

t=[0:0.3:2*%pi]';

Z=sin(t)*cos(t');

plot3d(t,t,Z);

Так как у нас две функции зависят от одной переменной, то дважды указываем параметр t.

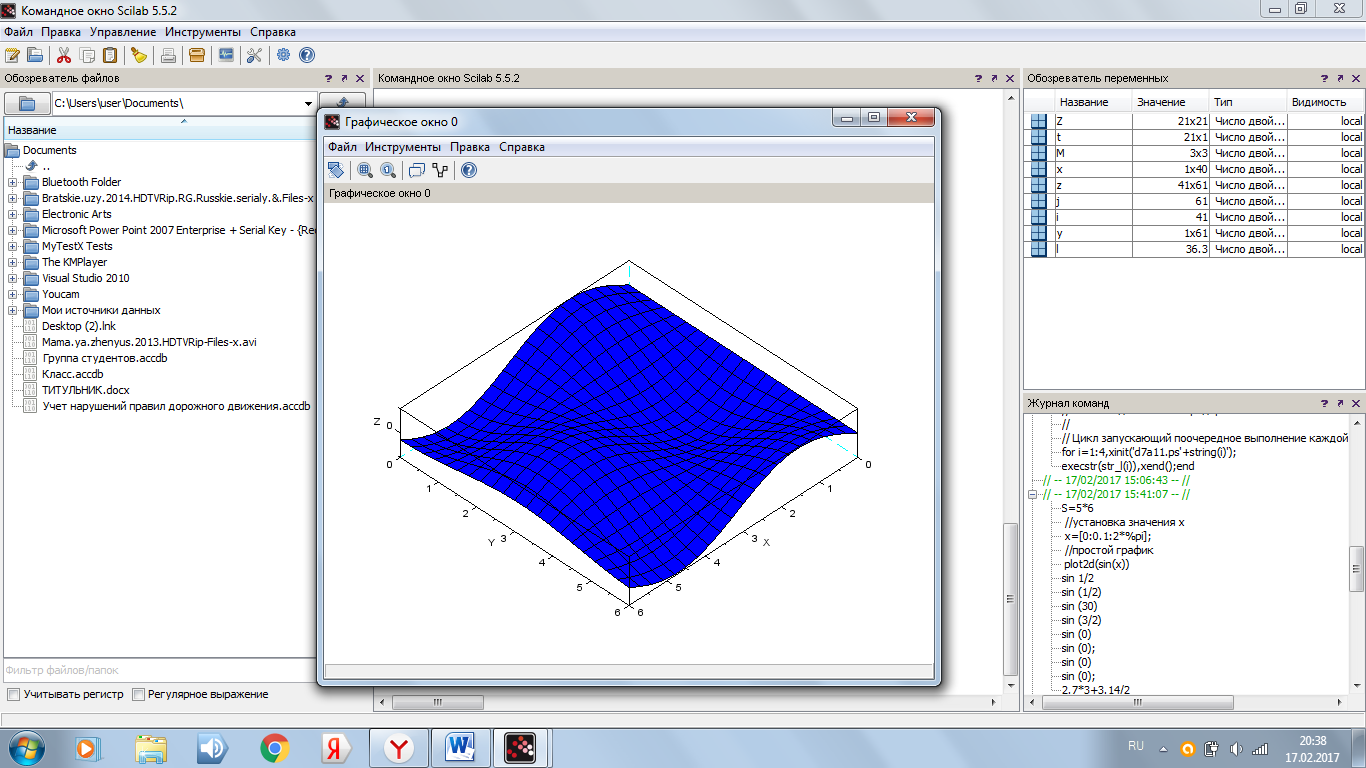
Рисунок 3. Результат программы с помощью функции plot3d

Построим поверхность, уравнение которой задается двумя независимыми переменными.

Задача 2. Построить график функции 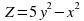при помощи команды plot3d1

Прежде всего, зададим массивы X и Y. Затем сформируем матрицу значений функции Z (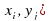, используя оператор цикла for. Здесь i параметр цикла, который будет перебирать все значения массива, а j параметр цикла который будет сопоставлять каждого значению массива X по очереди все значения массива Y.

Таким образом, сначала будут вычислены все значения функции Z при меняющемся Y (от первого до последнего значения в массиве) и первом значении массива X. Затем при втором значении массива X и т. д. Здесь используем функцию length, она определяет количество элементов массива X (Y). Наконец для построения поверхности обратимся к функции plot3d1 (см. рис.3).

x=[-2:0.1:2];

y=[-3:0.1:3];

for i=1:length(x)

for j=1:length(y)

z(i,j)=5*y(j)^2-x(i)^2;

end

end

plot3d1(x',y',z,-125,51);

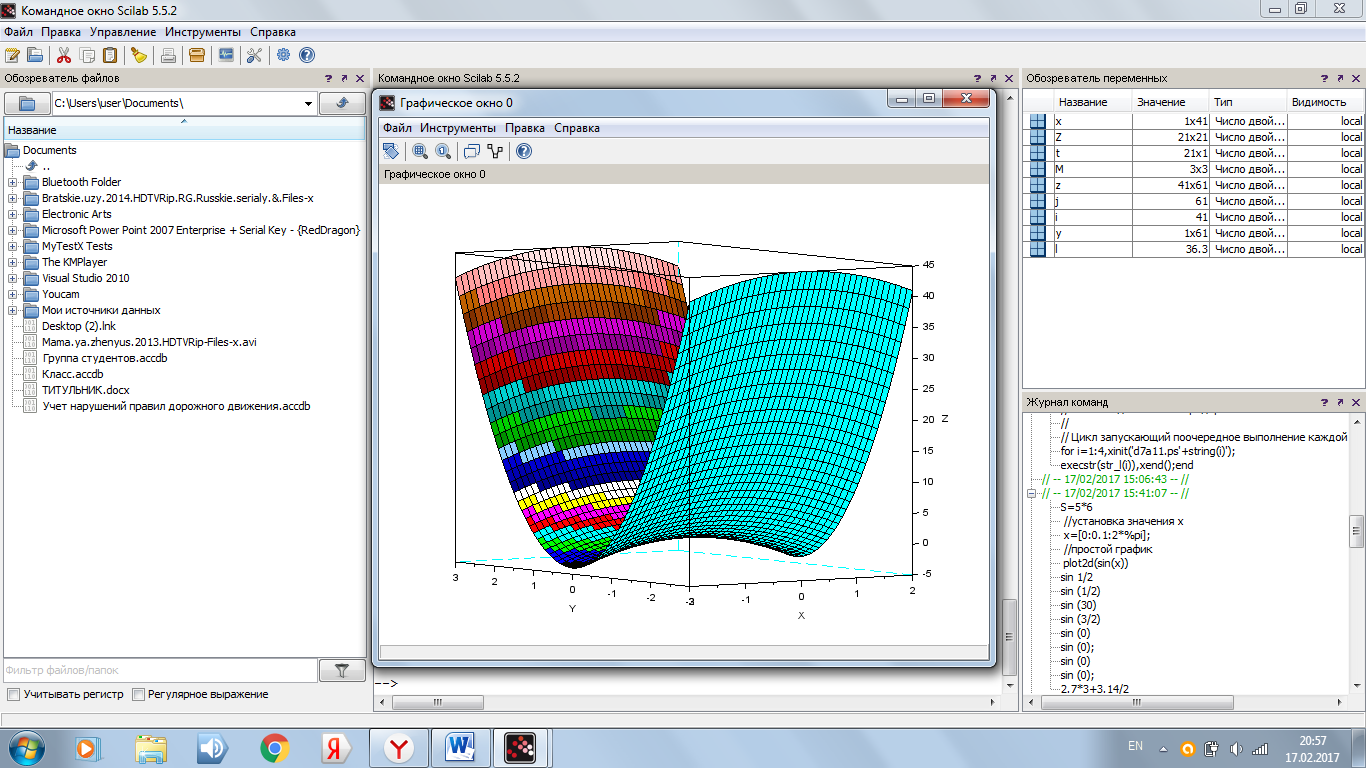
Рисунок 4. Результат программы с помощью функции plot3d1

Существуют также и другие функции, рассмотрим некоторые из них:

1. meshgrid (для формирования сетки);

2. mesh и surf (для построения графиков);

3. plot3d2 и plot3d3 (построение графиков поверхностей, заданных параметрически);

4. param3d (построение трехмерной линии, заданной параметрически).

Рассмотрим построение 3-х мерного графика на следующем примере функции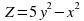, 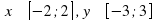. Для формирования сетки воспользуемся функцией meshgrid.

[x y]=meshgrid(-2:2,-3:3)

//Здесь -2:2 -массив, определяющий сетку по Х,

// -3:3 – массив, определяющий сетку по Y

[x y]=meshgrid(-2:0.1:2,-3:0.1:3);

z=5*y.^2-x.^2;

mesh(x,y,z); (см. рис. 5)

Функция surf строит каркасную поверхность, заливая ее каждую клетку цветом, который зависит от значения функции в узлах сетки (см. рис. 6).

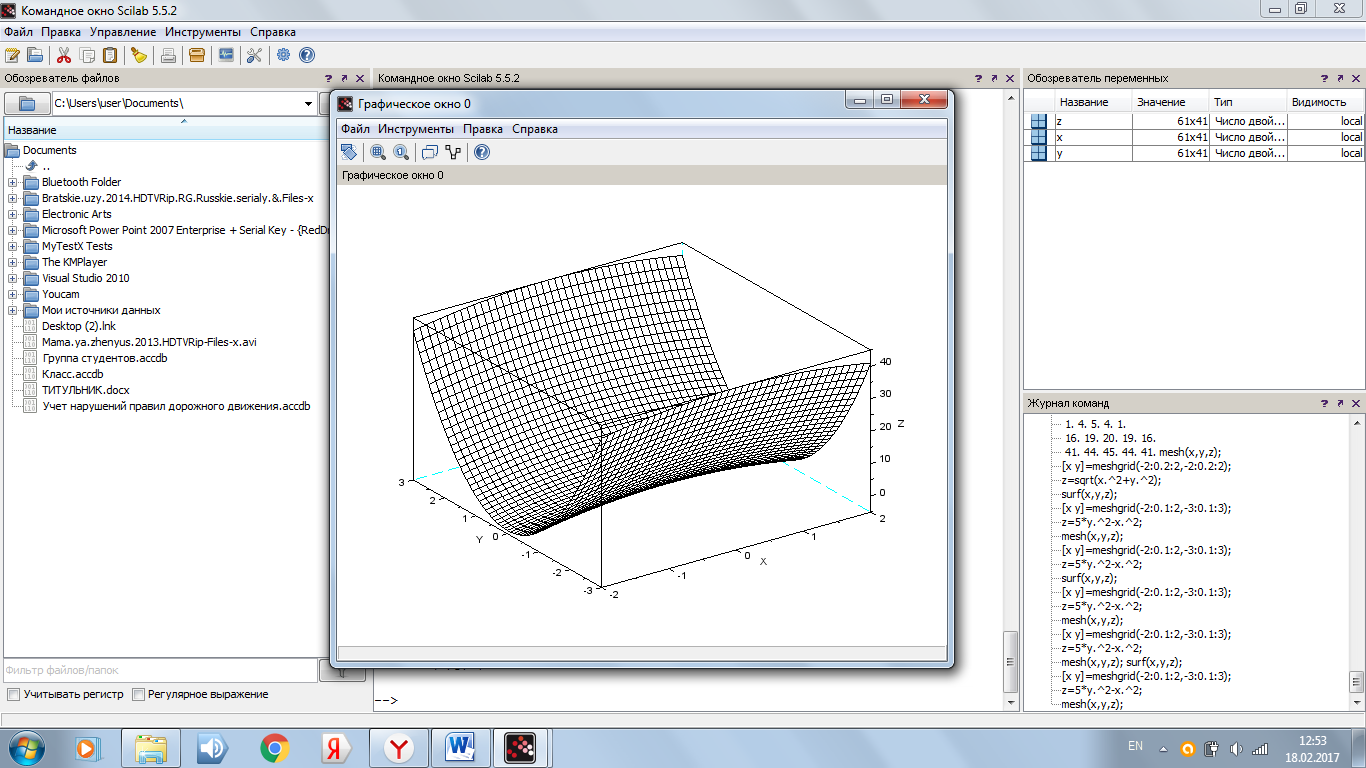
Рисунок 5. График функции, построенный с помощью функции mesh

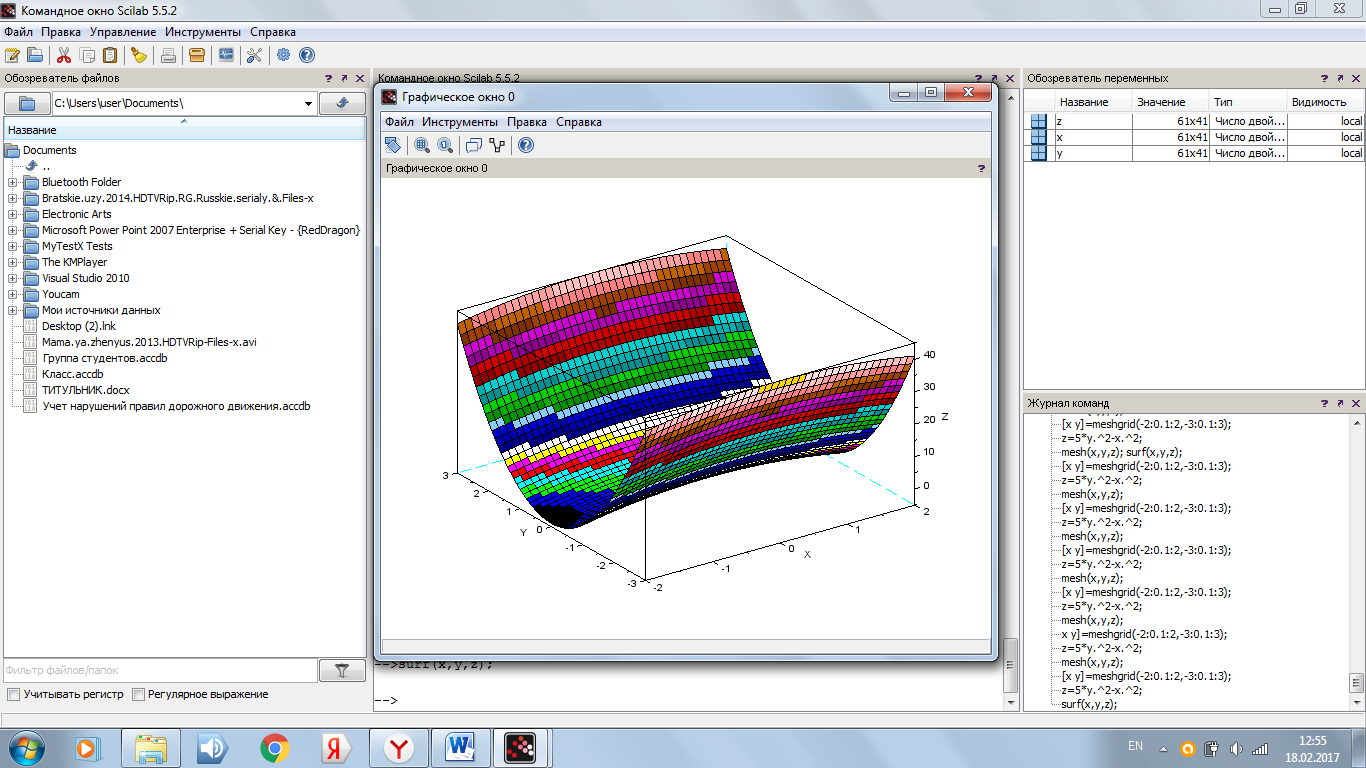
Рисунок 6. График функции, построенный с помощью функции surf

Рассмотрим функцию .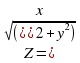

[x y]=meshgrid(-2:0.2:2,-2:0.2:2);

z=sqrt(x.^2+y.^2);

surf(x,y,z);

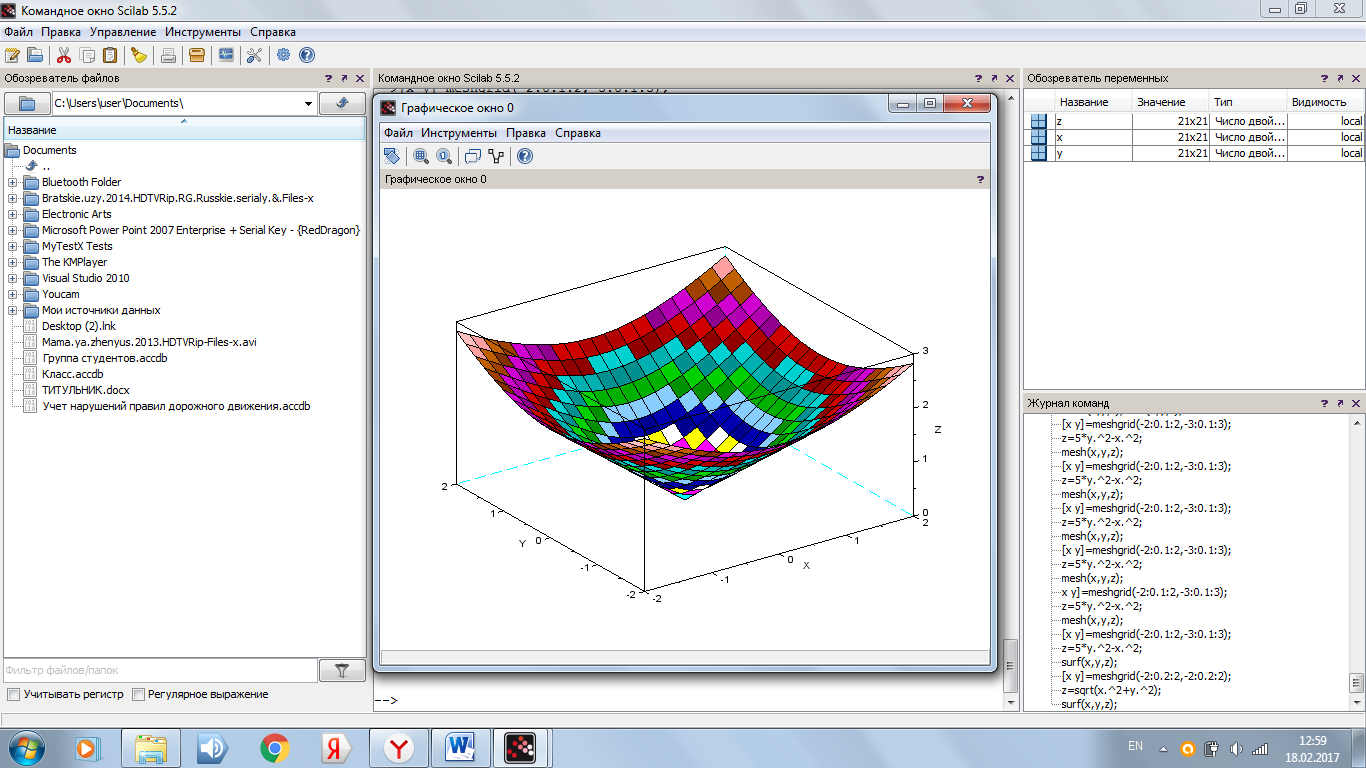
Рисунок 7. График функции 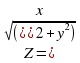, построенный с помощью функции surf

В Scilab можно построить графики двух поверхностей в одной системе координат, для этого, как и для плоских графиков следует использовать команду mtlb_hold('on'), которая блокирует создание второго нового окна при выполнении команд surf или mesh. Построить график функции 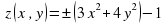. Результат программы представлен ниже на рисунке 8.

[x y]=meshgrid(-2:0.2:2,-2:0.2:2);

z=3*x.^2+4*y.^2-1;

z1=-3*x.^2-4*y.^2-1;

surf(x,y,z);

mtlb_hold('on');

surf(x,y,z1);

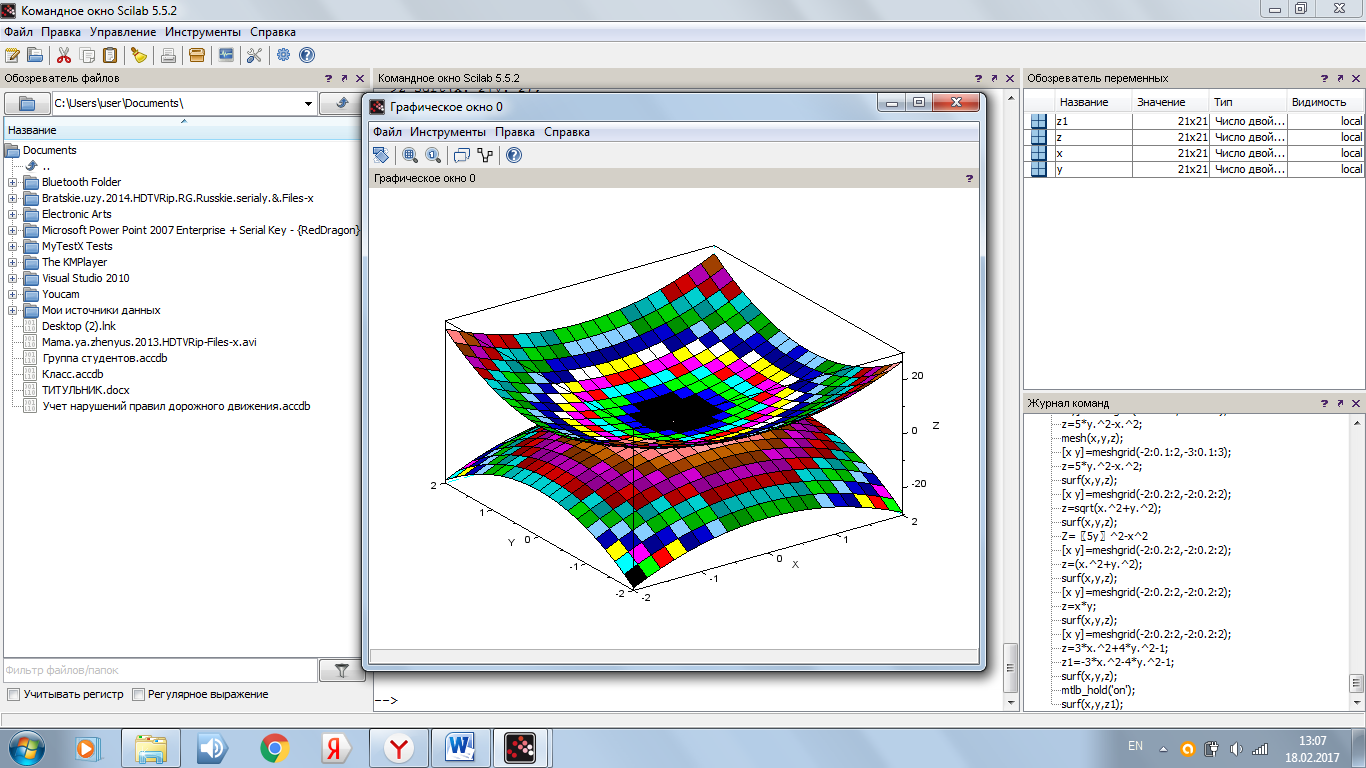
Рисунок 8. Результат программы

1. Построение графиков поверхностей, заданных параметрически

Рассмотрим задачу построения графика поверхности сферы x(u,v)=cos(u)cos(v), y(u,v)= cos(u)sin(v), z(u,v)=sin(u) (см. рис. 9)

u = linspace(-%pi/2,%pi/2,40);

v = linspace(0,2*%pi,20);

X = cos(u)'*cos(v);

Y = cos(u)'*sin(v);

Z = sin(u)'*ones(v);

plot3d2(X,Y,Z);

// Подпись графика

xtitle('Function w=exp(sin(x))','X','Y','Z');

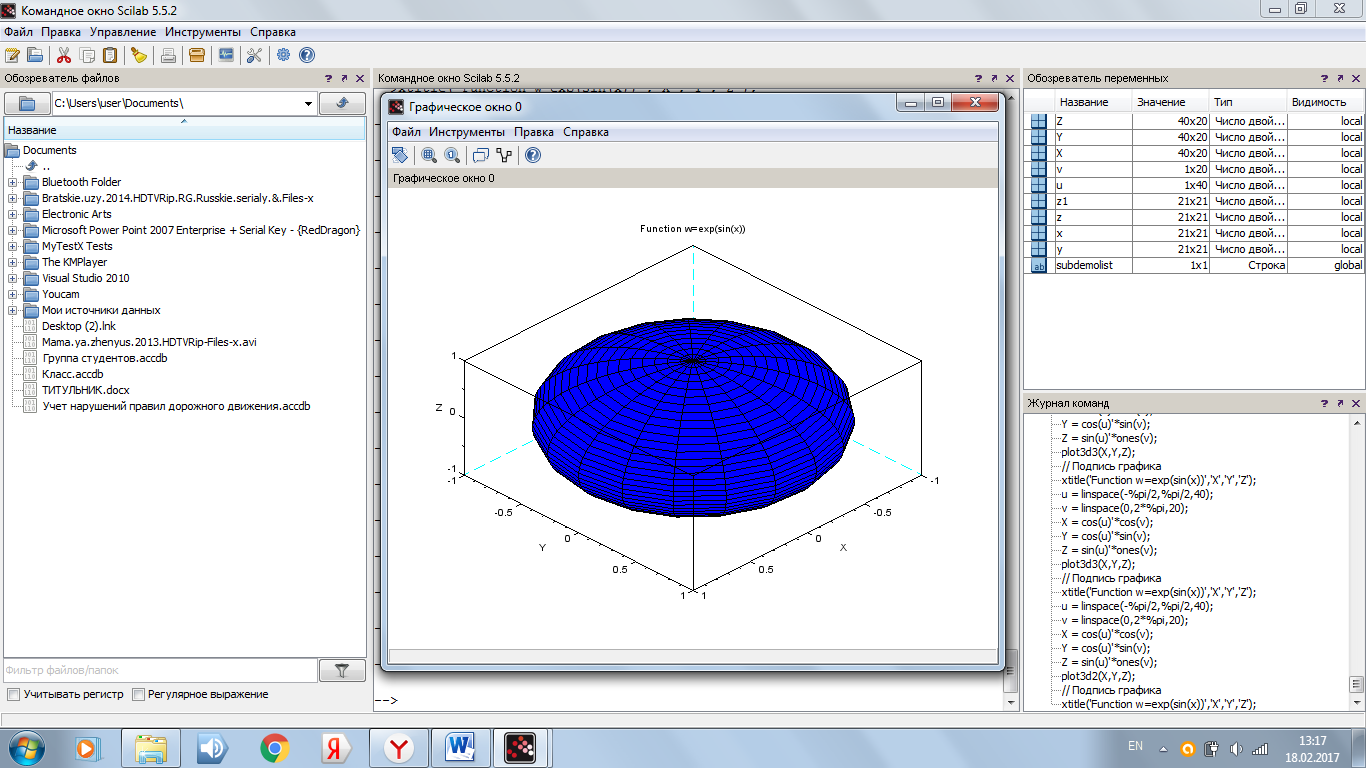
Рисунок 9. Результат программы с функцией plot3d2

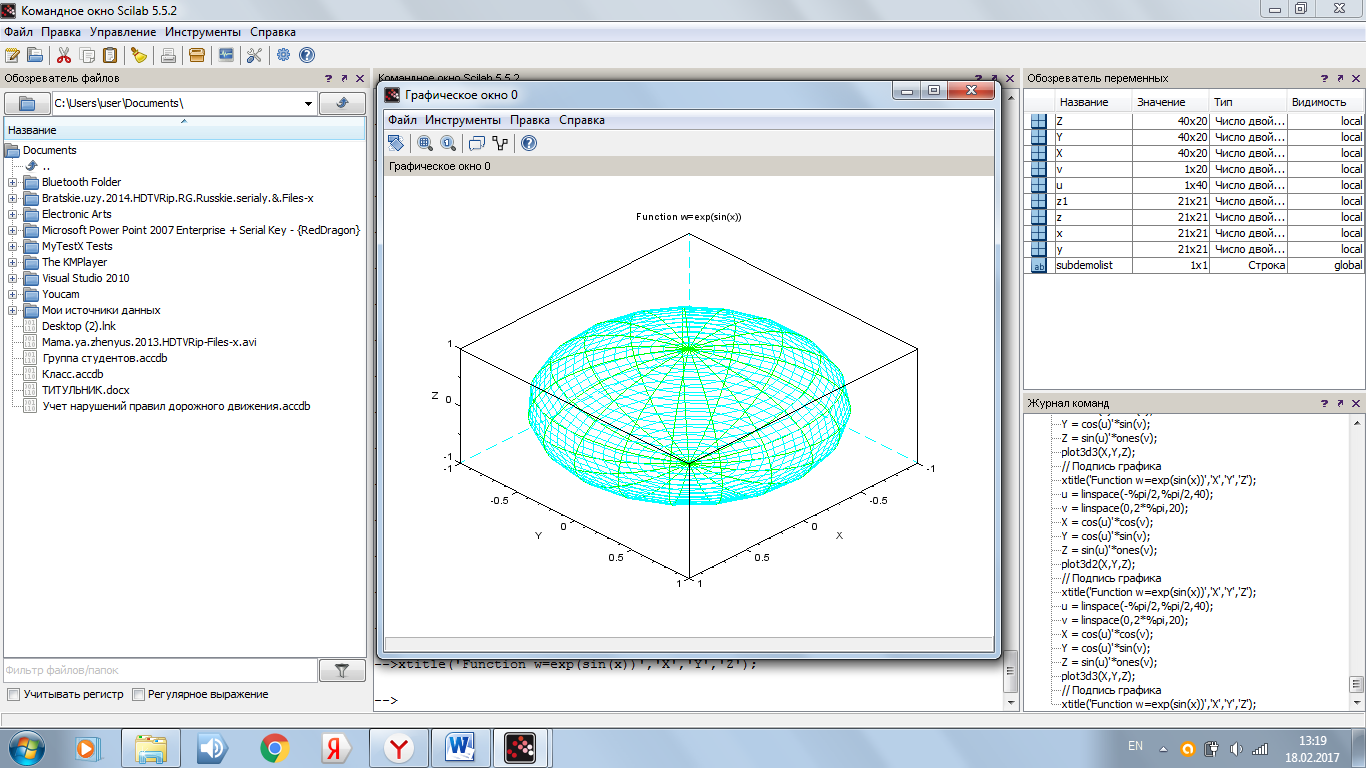
Рисунок 9. Результат программы с функцией plot3d3

1. Построение трехмерной линии, заданной параметрически

В качестве примера рассмотрим построение трехмерной линий, заданной уравнением x(t)=sin(t), y (t)=cos(t), z (t)= t/10 . (см. рис. 10)

t = 0:0.1:10*%pi;

param3d(sin(t),cos(t),t/10,45,35);

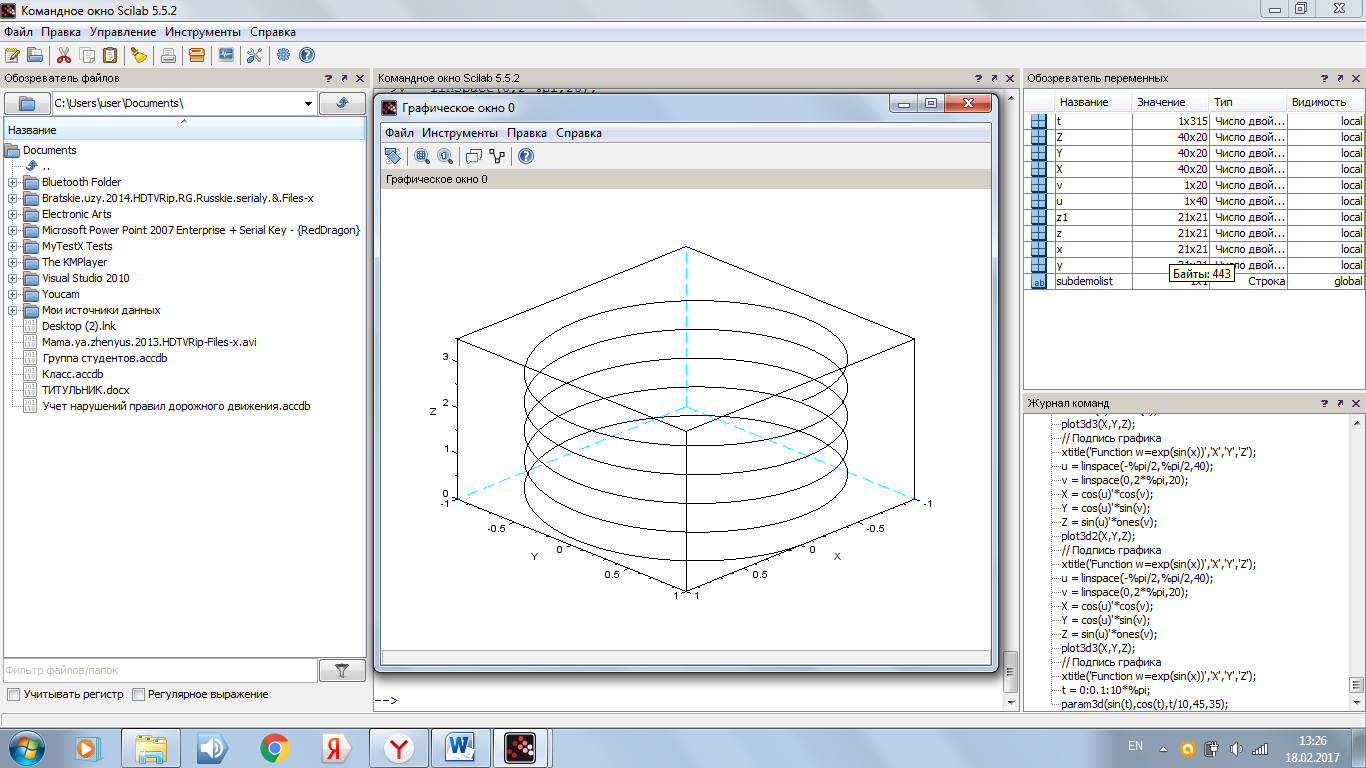
Рисунок 10. Результат программы с функцией param3d

Список использованной литературы

1. Алексеев, Е.Р., Чеснокова, О.В. Scilab теория и практика. Донецк – 2007. – 159с.

2. Андриевский А.Б., Андриевский Б.Р., Капитонов А.А., Фрадков А.Л. РЕШЕНИЕ ИНЖЕНЕРНЫХ ЗАДАЧ В SCILAB – С.Питербург. – 97 с.

3. Бакусов, Л. М., Кондратьева, О. В. Решение задач оптимизации средствами Scilab и Excel. – Уфа. – 2011. – 33 с.

4. http://teacher.ucoz.net/Lection/Scilab/glava_5.pdf

5. Сайт для скачивания программы Scilab: https://ru.vessoft.com/software/windows/download/scilab