3d построения в mathcad

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ

ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ «МОРДОВСКИЙ ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ

ИНСТИТУТ ИМЕНИ М. Е. ЕВСЕВЬЕВА»

Физико-математический факультет

Кафедра информатики и вычислительной техники

РЕФЕРАТ

3D ПОСТРОЕНИЯ В MATHCAD

Выполнила студентка группы МДМ-113

Романчукова Елена Ивановна

Проверила: Т. В. Кормилицына,

канд. физ.-мат. н., доцент

Саранск 2018

Введение 3

Система компьютерной математики MathCad 4

Интерфейс пользователя в MathCad 5

Графика в трехмерном пространстве в MathCad 7

Построение трехмерного графика по массиву данных 8

Построение трехмерного графика по заданному аналитическому выражению 9

Построение трехмерной столбиковой диаграммы 10

Построение совокупности точек в трехмерном пространстве 10

Построение нескольких графиков в трехмерном пространстве 11

Список использованных источников 13

Mathcad – система компьютерной алгебры из класса систем автоматизированного проектирования, ориентированная на подготовку интерактивных документов с вычислениями и визуальным сопровождением, отличается лёгкостью использования и применения для коллективной работы.

Mathcad был задуман и первоначально написан Алленом Раздовом из Массачусетского технологического института(MIT), соучредителем компании Mathsoft, которая с 2006 годаявляется частью корпорации PTC (Parametric Technology Corporation).

Mathcad имеет интуитивный и простой для использования интерфейс пользователя. Для ввода формул и данных можно использовать как клавиатуру, так и специальные панели инструментов.

Несмотря на то, что эта программа, в основном, ориентирована на пользователей, не являющихся программистами, Mathcad также используется в сложных проектах, чтобы визуализировать результаты математического моделирования путём использования распределённых вычислений и традиционных языков программирования. Также Mathcad часто используется в крупных инженерных проектах, где большое значение имеет трассируемость и соответствие стандартам.

Mathcad достаточно удобно использовать для обучения, вычислений и инженерных расчето. Открытая архитектура приложения в сочетании с поддержкой технологий. NET и XML позволяют легко интегрировать Mathcad практически в любые ИТ-структуры и инженерные приложения. Есть возможность создания электронных книг (e-Book).

Mathcad содержит сотни операторов и встроенных функций для решения различных технических задач. Программа позволяет выполнять численные и символьные вычисления, производить операции со скалярными величинами, векторами и матрицами, автоматически переводить одни единицы измерения в другие.

Среди возможностей Mathcad можно выделить:

–решение дифференциальных уравнений, в том числе и численными методами;

–построение двумерных и трёхмерных графиков функций (в разных системах координат, контурные, векторные и т. д.);

–использование греческого алфавита как в уравнениях, так и в тексте;

–выполнение вычислений в символьном режиме;

–выполнение операций с векторами и матрицами;

–символьное решение систем уравнений;

–аппроксимация кривых;

–выполнение подпрограмм;

–поиск корней многочленов и функций;

–проведение статистических расчётов и работа с распределением вероятностей;

–поиск собственных чисел и векторов;

–вычисления с единицами измерения;

–интеграция с САПР-системами, использование результатов вычислений в качестве управляющих параметров.

С помощью Mathcad инженеры могут документировать все вычисления в процессе их проведения.

Mathcad относится к системам компьютерной алгебры, то есть средств автоматизации математических расчетов. В этом классе программного обеспечения существует много аналогов различной направленности и принципа построения. Наиболее часто Mathcad сравнивают с такими программными комплексами, как Maple, Mathematica, MATLAB.

Mathcad, в отличие от Maple, изначально создавался для численного решения математических задач, он ориентирован на решение задач именно прикладной, а не теоретической математики, когда нужно получить результат без углубления в математическую суть задачи.

Главное меню в математическом пакете Mathcad состоит из девяти пунктов, в каждом из которых объединены функционально однородные команды:

–Файл (File). Пункты данного меню отражают общие действия по работе с документами, такие как создание, открытие, сохранение и печать документов с результатами расчетов.

–Правка (Edit). В данном меню в Mathcad сосредоточены общие команды по редактированию документа или его фрагментов, такие как: вырезать; копировать; вставить; проверить орфографию; отменить ранее выполненное действие; найти заданный фрагмент и, если необходимо, заменить его на другой.

–Вид (View). Определяет вид интерфейса пользователя, то есть перечень и порядок расположения различных элементов, отображаемых на экране дисплея при работе в Mathcad. Данное меню управляет масштабом, отображением линеек, строкой состояния, набором активных панелей инструментов.

–Вставка (Insert). Позволяет ввести в документ различные элементы: матрицы; графики; функции; рисунки и компоненты других программных приложений, например, Excel, MatLab.

–Формат (Format). Задает формат стиля, шрифта текста, абзаца. Позволяет установить вид формул и формат отображения результатов расчета.

– Математика (Math). Содержит команды, обеспечивающие проведение расчетов и задание опций, определяющих их точность.

–Символика (Symbolics). Включает команды выполнения различных символьных расчетов.

– Окно (Window). Команды данного меню активизируют различные документы и определяют режимы их отображения на экране дисплея.

–Помощь (Help). Команды данного меню позволяют получить инструкции по работе с математической системой Mathcad, а также вызвать «Центр ресурсов», содержащий многочисленные примеры решения задач.

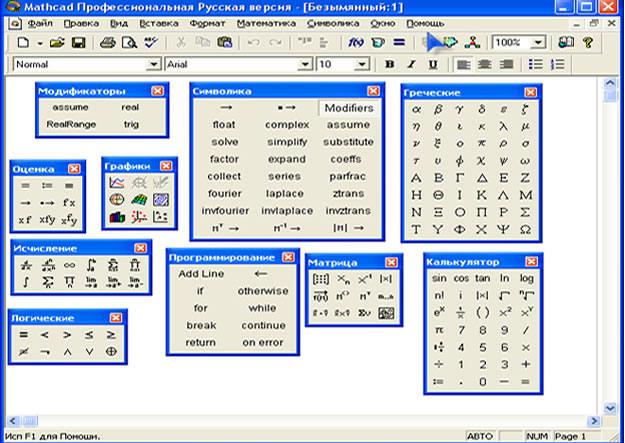
Рисунок 1 – Главное меню.

К стандартным панелям инструментов относятся панели инструментов «Стандартная» и «Форматирование», которые, как правило, по умолчанию активизируются при загрузке математической системы Mathсad. Кроме того, к стандартным панелям относится панель инструментов «Математика», содержащая ссылки на панели инструментов семейства «Математические».

К семейству панелей инструментов «Математические» относятся девять панелей инструментов (панель инструментов «Модификаторы» является дополнением панели инструментов «Символика»). Эти панели инструментов отображены на рис. в рабочей области Mathсad. Каждая из панелей содержит набор кнопок, позволяющих ввести определенные математические операторы и символы, задать вычислительные операции и действия при вводе математических выражений или при проведении расчетов.

В нижней части рабочей области расположена строка состояния, которая содержит общую служебную информацию. При перемещении курсора мыши в определенную область в левой части строки состояния выводится оперативная справка о предполагаемых действиях пользователя.

Трехмерная графика – одна из наиболее привлекательных сторон Mathcad. Вы можете построить трехмерные графики следующих типов:

Surface Plot [Ctrl]+2 – трехмерный график;

Contour Plot [Ctrl]+5 – карта линий уровня;

3D Scatter Plot – изображение совокупности точек в трехмерном пространстве;

3D Bar Plot – трехмерная гистограмма;

Vector Field Plot – векторное поле.

Вы можете выбрать тип графика, который надо построить одним из трех способов:

1) из подменю InsertGraph;

2) через панель инструментов – кнопкой “Graph Toolbar” открыв графическую палитру и выбрав из нее нужный тип графика;

3) через клавиатуру:

[Ctrl]+2 – построить трехмерный график;

[Ctrl]+5 – построить карту линий уровня.

Построенный график вы можете изменить в соответствии с вашим желанием: отодвинуть или приблизить, изменить масштаб, повернуть, изменить способ окраски поверхности, спрятать скрытые линии или показать их и т.д.

Рассмотрим более подробно процесс построения и редактирования различных трехмерных графиков.

Для того, чтобы построить поверхность по массиву данных, проделайте следующие действия:

1. Задайте размерность матрицы, по которой будет построен график (т.е. область изменения индексов для x и y).

2. Введите выражения, по которым вычисляются x и y (причем в эти выражения должны входить заданные ранее индексы).

3. Задайте аналитическое выражение функции двух переменных x и y, а затем определите матрицу на основе этой функции. Номер строки определяет значение x, номер столбца – значение y, а сам элемент матрицы – значение z, т.е. высоту над плоскостью xy.

4. Создайте поле трехмерного графика одним из трех способов:

а) через подменю InsertGraphSurface Plot;

б) через панель инструментов – кнопкой «Graph Toolbar» открыв графическую палитру и выбрав из нее тип графика «Surface Plot»;

в) через клавиатуру – [Ctrl]+2.

1. Введите вместо маркера ввода имя матрицы, содержащей набор данных, и щелкните мышью вне поля графика. После этого на экране появится поверхность, построенная по массиву данных (рис. 2).

Замечание. Если у вас уже есть массив данных, введите его в виде матрицы или импортируйте из другого приложения, а затем выполните п.4.

Рассмотрим пример построения поверхности по массиву данных.

Пример 1.

1. Диапазон изменения индексов:

2. Зададим x и y:

3. Определим f(x,y) и матрицу М:

4. Построим график:

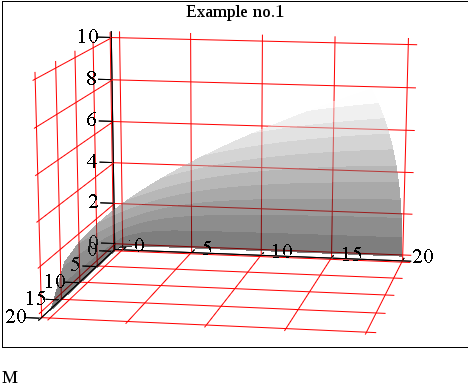
Рисунок 2 – Пример построения поверхности по массиву данных.

Вы можете построить трехмерный график не только по заданному массиву данных, но и по аналитическому выражению – функции двух переменных. Для этого:

1. Запишите выражение, определяющее функцию двух переменных. Оно может быть как скалярным (пример 2) так и векторным (пример 3).

2. Создайте поле трехмерного графика одним из трех способов:

а) через подменю InsertGraphSurface Plot;

б) через панель инструментов – кнопкой «Graph Toolbar» открыв графическую палитру и выбрав из нее тип графика «Surface Plot»;

в) через клавиатуру – [Ctrl]+2.

1. Введите вместо маркера ввода имя функции (аргументы указывать не надо) и щелкните мышью вне поля графика. После этого на экране появится поверхность, построенная по заданной вами функции (рис.3).

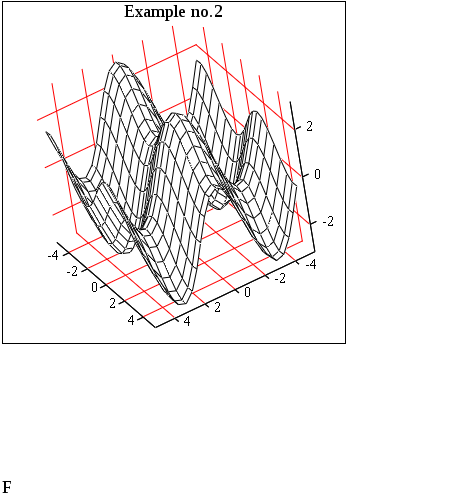
Рисунок 3 – Построение поверхности по аналитическому выражению в скалярной форме

Трехмерный объект можно представить не только в виде поверхности (рис.2), но и в виде трехмерной столбиковой диаграммы. Для ее построения требуется выполнить следующие действия:

1. Задайте матрицу или функцию двух переменных, по которой надо построить график.

2. Создайте поле графика одним из двух способов:

а) через подменю InsertGraph3D Bar Plot;

б) через панель инструментов – кнопкой «Graph Toolbar» открыв графическую палитру и выбрав из нее тип графика «3D Bar Plot».

1. Введите вместо маркера ввода имя функции или матрицы и щелкните мышью вне поля графика. После этого на экране появится трехмерная столбиковая диаграмма, построенная по заданной вами функции.

Если имеющийся массив данных вы хотите представить в виде точек в трехмерном пространстве, а не интерполировать его для построения поверхности, сделайте следующее:

1. Задайте три вектора или матрицы, определяющие x-, y- и z-координаты точек, соответственно. Число элементов в этих векторах лил матрицах равно числу точек, которые будут выведены на график. Вы также можете задать три функции одной или двух переменных.

2. Создайте поле графика одним из двух способов:

а) через подменю InsertGraph3D Scatter Plot;

б) через панель инструментов – кнопкой «Graph Toolbar» открыв графическую палитру и выбрав из нее тип графика «3D Scatter Plot».

1. Введите вместо маркера ввода в круглых скобках имена трех векторов или матриц, разделяя их запятыми и щелкните мышью вне поля графика. После этого на экране появится совокупность точек в трехмерном пространстве, построенная по заданным вами векторам или матрицам.

Вы можете построить в трехмерный график не только по заданному массиву данных, но и по аналитическому выражению – функции двух переменных. Для этого:

1. Задайте два массива данных или две функции двух переменных, по которым надо построить графики.

2. Создайте поле трехмерного графика одним из трех способов:

а) через подменю InsertGraphSurface Plot;

б) через панель инструментов – кнопкой «Graph Toolbar» открыв графическую палитру и выбрав из нее тип графика «Surface Plot»;

в) через клавиатуру – [Ctrl]+2.

1. Вместо маркера ввода введите (через запятую) имена матриц или функций и щелкните мышью вне поля графика. После этого в поле графика появятся две поверхности, построенные по заданным вами функциям или матрицам (рис. 4).

В следующем примере вы увидите пересечение поверхности, представленной на рис. 4 с плоскостью H(x,y) = x.

Пример 2. 1. Определим две функции двух переменных : 2. Построим график:

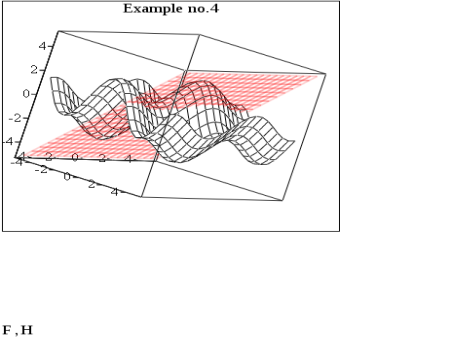
Рисунок 4 – Построение двух поверхностей в трехмерном пространстве

Замечание. В одном поле трехмерного графика можно построить не только две поверхности, но и совместить поверхность с картой линий уровня (например, вы можете поместить на один график саму поверхность и ее проекцию на плоскость xy).

1. Акишин, Б. А. Прикладные математические пакеты. Часть 1. MathCAD / Б. А. Акишин, Н. Х. Эркенов. – СПб. : РадиоСофт, 2009. – 132 с.

2. Алексеев, Е. Р. Mathcad 12 / Е. Р. Алексеев, О. В. Чеснокова. – М.: НТ Пресс, 2005. – 352 с.

3. Афонькина, М. Л. Проблема точности вычислений в системах компьютерной математики [Текст] / М. Л. Афонькина // Проблемы и перспективы развития информационных и коммуникационных технологий в образовании и науке: межвузовский сборник научно-методических трудов студентов, аспирантов и молодых ученых / МордГПИ. – Саранск, 2014. – 183с.

4. Бидасюк,  Ю. М. MathsoftMathCAD 11. Самоучитель / Ю.М. Бидасюк. – СПб. : Диалектика, 2004. – 224 с.

5. https://ru.wikipedia.

6. https://studfiles.net/preview/2479912/page:2/