Уравнение
Цели урока:
1) Обучающая: формировать представления об уравнении, корне уравнения, решении уравнений; организовать деятельность, направленную на выполнение учебных заданий, связанных с решением уравнений вида: х + а = b, x — a = b, a — x = b и приводимых к ним; создать условия для расширения знаний математических понятий и формирования новых знаний.
2) Развивающая: содействовать развитию и обогащению словарного запаса.
3) Воспитывающая: содействовать расширению кругозора.
Тип урока: изучение нового материала с первичным закреплением.
План урока:
1. Организационный этап.
2. Актуализация опорных знаний.
3. Этап получения новых знаний.
4. Этап обобщения и закрепления нового материала.
5. Рефлексия.
6. Заключительный этап.
Форма урока: Видеоматериал с элементами практикума.
Ход урока:
1. Организационный этап.
Здравствуйте. Прежде чем мы приступим к уроку, хотелось бы узнать, ваше настроение и как вы настроены к работе на уроке.
2. Актуализация опорных знаний:
На предыдущих уроках мы с вами решали задачи способом моделирования условия задачи отрезками, и в ходе решения составляли выражения для нахождения неизвестного числа.
3. Этап получения знаний:
Тема нашего урока «Уравнение». На этом уроке мы узнаем такие понятия как уравнение, корень уравнения. А также научимся составлять и решать уравнения.
В математике принято и очень удобно обозначать неизвестное число буквой, затем составлять равенство и решать это равенство. Рассмотрим задачу: Лере задали прочитать рассказ. Она прочитала этот рассказ за два дня. В первый день Лера прочитала 40 страниц. Сколько страниц прочитала Лера за второй день, если известно, что весь рассказ состоял из 65 страниц?
Решение: Для наглядности внесем известные нам данные в таблицу. Мы знаем, что за первый день Лера прочитала 40 страниц, и знаем, что всего 65 страниц в рассказе. Обозначим буквой х неизвестное количество страниц, которые Лера прочитала за второй день. Составим равенство по известным нам данным. Мы к страницам, прочитанным за первый день (40), прибавим количество прочитанных страниц за второй день (х), и это будет равно количеству всех страниц в рассказе (65). Получили равенство: 40 + х = 65. Нам надо найти такое значение х, при котором будет выполняться это равенство. По смыслу вычитания, чтобы найти неизвестное слагаемое мы должны от известной суммы отнять известное слагаемое.

Равенство 40 + х = 65 называют уравнением.
Уравнение - это равенство, содержащее букву, значение которой надо найти.
Значение буквы, при котором из уравнения получается верное числовое равенство, называют корнем уравнения.
Например, корнем уравнения 40 + х = 65 является число 25.
Если в равенство входит буква, то оно может быть верным при одних значениях этой буквы и неверным при других ее значениях. Например, уравнение 40 + х = 65 при х = 25 — верно, подставим вместо х значение 25, видим, что равенство выполняется верно. А при х = 15 — это равенство будет уже неверным, т.к. при замене х на число 15 равенство 40 + 15 никак не может быть равно 65.
Иногда надо узнать, является ли данное число корнем уравнения или нет. Тогда его не надо решать, нужно просто подставить предлагающиеся числа вместо неизвестного числа. Если получится верное равенство, то это данное число и есть корень уравнения, если равенство неверно — число не является корнем. Например, выполним задание: какое из чисел 3, 5 или 7, является корнем уравнения х + 7 = 12? Подставим по очереди каждое данное нам число. При х = 3 получаем равенство 3+7 равно оно 10, что в свою очередь не равно 12. При х = 5, получаем 5+7=12. При х = 7, получаем 7+7=14 и ≠12. При подстановке чисел мы убедились, что только число 5 дает в сумме с числом 7 верное равенство.
Решить уравнение — значит найти все его корни, или убедиться, что уравнение не имеет корней.
Запишите полезные правила для решения некоторых уравнений:

1. Нахождение неизвестного слагаемого:
a + x = b, где a и b — любые натуральные числа. Если нам неизвестно второе слагаемое, то мы должны из суммы вычесть первое слагаемое,
x + a = b. Если нам неизвестно первое слагаемое, то мы должны от суммы отнять второе слагаемое,
2. Нахождение неизвестного уменьшаемого:
x — a = b. Если нам неизвестно уменьшаемое, то мы должны к разности прибавить вычитаемое,
3. Нахождение неизвестного вычитаемого:
a — x = b. Если нам неизвестно вычитаемое, то мы должны от уменьшаемого отнять разность,
4. Этап обобщения и закрепления нового материала.
Итак, сделаем основные выводы: на этом уроке мы узнали, что такое уравнение, корень уравнения. Научились составлять уравнения и решать их.
Для закрепления материала ответьте на вопросы:
— Какое равенство называют уравнением?
— Какое число называют корнем уравнения?
— Что означает требование Решить уравнение?
— Как проверить, является ли определенное число корнем данного уравнения?
— Как найти неизвестное слагаемое (уменьшаемое, вычитаемое)?
5. Рефлексия.
Были ли трудности при работе на уроке? Если да, то какие?
Получите комплекты видеоуроков + онлайн версии
Похожие записи
 38113
38113 Нравится
0
Нравится
0

 Получите свидетельство
Получите свидетельство Вход
Вход







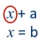


Непременно поделюсь им с детьми!
Всех благ главному кулинару умных идей!
Спасибо!