Повторим формулировку основного свойства дроби.
Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.
Например
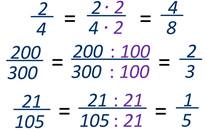
Обратите внимание, с помощью основного свойства дроби можно упрощать дроби, заменяя одну дробь другой, равной данной, но с меньшим числителем и знаменателем.
Например

Такое преобразование называется сокращением дроби.
Определение
Деление числителя и знаменателя дроби на одно и то же, не равное нулю, число, называется сокращением дроби.
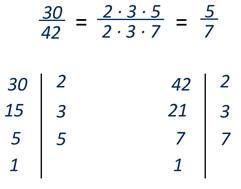
Либо можно сократить дробь сразу на 6.
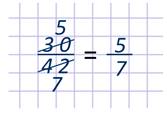
Не всякую дробь можно сократить!
Например

Определение
Значит, сокращение дроби можно провести тогда и только тогда, когда её числитель и знаменатель не являются взаимно простыми числами.
Если же числитель и знаменатель дроби взаимно просты, то дробь сократить нельзя.
Такие дроби называются несократимыми дробями.
Например

Задание
Сократить дробь 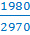 .
.
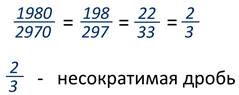
Сокращение закончено.
Кроме того, сокращение дробей можно упростить с помощью нахождения НОДа числителя и знаменателя дроби.
Например

Значит, дробь 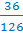 можно
сократить на 18. Получим
можно
сократить на 18. Получим
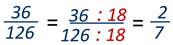
Задание
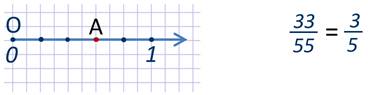
Отметим на координатном луче точку А с координатой 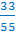 .
.
Итоги
Деление числителя и знаменателя дроби на одно и то же, не равное нулю, число, называется сокращением дроби.
Если же числитель и знаменатель взаимно просты, то дробь сократить нельзя. Такие дроби называются несократимыми дробями.

 Получите свидетельство
Получите свидетельство Вход
Вход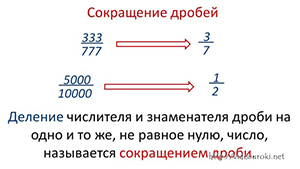



 0
0 6012
6012

