
- Привет, Плюс. А чем это ты занимаешься?
- Здравствуй, Минус. Понимаешь, меня пригласила в гости буква И. Ведь мы с ней в какой-то степени родственники.
- Интересно, а что общего может быть между математическим знаком и какой-то там буквой?
- Очень просто. Буква И так же как и я может объединять предметы. Ведь можно сказать, например, пять плюс два, а можно - пять и два. Все равно результат будет один и тот же.

- Понял. Ну а вот этот план-то тут при чем?
- Видишь ли, буква И живет за пределами нашего царства. Дорога предстоит долгая. Но дело в том, что к букве И можно добраться по двум разным дорогам. Вот посмотри. Передо мной точный подробнейший план местности по дороге в царство букв. И я пытаюсь понять, какая из этих двух дорог наиболее короткая.
- А чего тут думать! Ты посмотри - дороги состоят из отрезков. Такое впечатление, будто были прямые, а их кто-то поломал. Так они поломанными и остались.
- Не поломанными, а ломаными. Такие линии, состоящие из нескольких отрезков, в которых конец первого отрезок является началом второго, конец второго является началом третьего и так далее, называется ломаными линиями.
- Ну вот, ты сам и подсказал себе, как узнать, какая дорога короче. Ведь каждая дорога состоит из отрезков, а находить длину отрезков мы уже умеем.
- Ой, точно! Спасибо минус. А то я сидел-сидел и ничего придумать не мог. Кстати, отрезки в ломаной линии принято называть звенья, а места соединения звеньев между собой - это вершины.
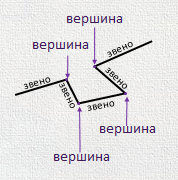
Итак, можно измерить длины ломаных, используя линейку.
Измерим длину каждого звена:
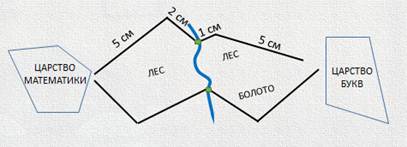
Получим длину всей дороги:
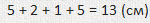
А вот вторую дорогу я измерю по-другому.
- А что, есть еще какой-то другой способ нахождения длины ломаной?
- Да, и здесь нам понадобятся и линейка, и циркуль. Для начала рисуем прямую, потом берем циркуль и измеряем длину первого звена и откладываем полученный результат на прямой. Затем так же измеряем остальные отрезки и так же откладываем на прямой, не забывая, что конец первого отрезка является началом второго, конец второго отрезка - это начало третьего и, конечно, конец третьего отрезка является началом четвертого.
А теперь измерим линейкой длину получившегося отрезка, составленного из четырех:
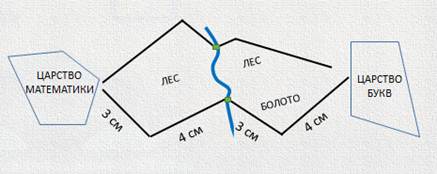
Получаем:
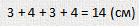
Странно, казалось, что этот второй путь короче. Давай-ка, я еще раз его перемерю линейкой. Так, действительно верно. Теперь я точно знаю, что, если пойду первой дорогой, то быстрее дойду в гости к букве И. Ведь её длина на плане - 13 сантиметров.
- Запомни, Плюсик. Длину ломаной на глазок не определишь. Для того чтобы измерить длину ломаной, надо измерить длину каждого звена, и результаты сложить.
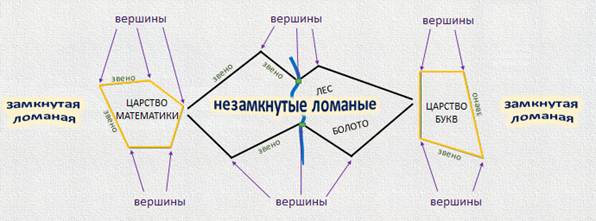
- Да, дорогой Минус. Я это теперь хорошо запомнил. Но вот еще что меня заинтересовало. Если внимательно посмотреть на план, то можно увидеть, что не только дороги, но и контуры царств тоже представляют из себя ломаные линии.
- Да, действительно. А я этого и не заметил. Я думал, что границы нашего царства математики просто имеет форму пятиугольника, а границы царства букв - четырехугольника.
- Все верно. Но и четырехугольник и пятиугольник состоят из ломаных линий. Правда, в отличие от дорог, эти линии полностью отгораживают свое внутреннее пространство, как бы закрывая, замыкая его. Внутрь попасть просто так невозможно. Поэтому подобные ломаные так и называются - замкнутые ломаные. А такие ломаные, как дороги, называются незамкнутыми, то есть не закрытыми.
- Ух ты, как много сегодня узнали. Теперь мы знаем, что:
· ломаная состоит из отрезков, которые называются звенья;
· точки, в которых соединяются звенья ломаной, называются вершинами;
· чтобы найти длину ломаной, надо измерить все её звенья и результаты сложить;
· ломаные бывают незамкнутые и замкнутые.
- Ну что же, пора мне в дорогу отправляться. Буква И, наверное, уже заждалась. До свидания, Минус.
- Счастливого пути. Возвращайся скорее.
- Не скучай, мой друг, скоро увидимся.

 Получите свидетельство
Получите свидетельство Вход
Вход



 0
0 2977
2977

