Вопросы занятия:
· ввести понятия «уравнение с одной переменной», «решение уравнений с одной переменной»;
· разобрать что значит «решить уравнение»;
· ввести понятие равносильных уравнений.
Материал урока
Рассмотрим следующую задачу.
К заданному числу прибавили 9 и получили в сумме 25. Какое число задумано?
Обозначим букой х задуманное число. Тогда по условию задачи
х + 9 = 25
То есть, чтобы найти неизвестное число, мы составили равенство, которое содержит переменную х. Равенства такого вида называются уравнениями с одной переменной.
Теперь надо найти такое значение переменной х, при подстановке которого в наше уравнение получается верное числовое равенство. Для этого переносим 9 в правую часть равенства и получаем:
х = 25 – 9.
х = 16
То есть 16 и есть задуманное число.
Найденное значение переменной х называется решением уравнения, или корнем уравнения.
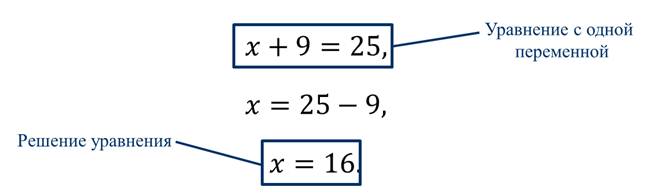
Таким образом, можем сформулировать следующие определения.
Равенство, содержащее одну переменную, называется уравнением с одной переменной, или уравнением с одним неизвестным.
Значение переменной, при котором уравнение превращается в верное числовое равенство, называется корнем (или решением) уравнения.
Рассмотренное выше уравнение имеет один корень.
Но есть уравнения, которые имеют два, три, четыре и более корней или не имеют корней вообще.
Например,

Определение.
Решить уравнение – это значит найти все его корни или доказать, что их нет.
Определение.
Два уравнения называются равносильными, если каждый корень первого уравнения является корнем второго, и наоборот – каждый корень второго уравнения является корнем первого, то есть, оба уравнения имеют одни и те же корни.
Равносильными являются также уравнения, которые не имеют корней.
Например,
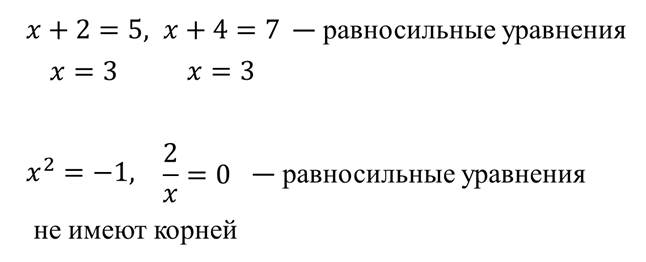
А теперь сформулируем свойства, которые используются при решении уравнений.
Свойство 1.
Если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получится уравнение, равносильное данному.
Например,
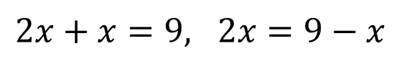
Свойство 2.
Также, если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнения, равносильное исходному.
Например,
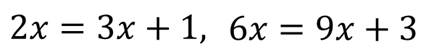
Давайте решим следующие упражнения.
Пример.

Пример.

Пример.

Пример.


 Получите свидетельство
Получите свидетельство Вход
Вход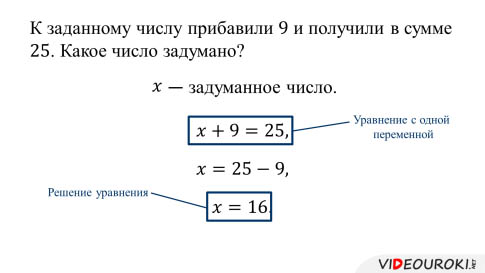



 0
0 19415
19415

