Ромб и квадрат

Давайте ещё раз вспомним, что параллелограмм – это четырёхугольник, у которого противоположные стороны попарно параллельны. А прямоугольник – это параллелограмм, у которого все углы прямые.

На этом уроке мы поговорим о таких геометрических фигурах как ромб и квадрат.

Итак, ромб – это параллелограмм, у которого все стороны равны.

Так как ромб является параллелограммом, то он обладает всеми его свойствами, о которых мы с вами говорили на предыдущих уроках.

Теорема. Свойства диагоналей ромба. У ромба диагонали взаимно перпендикулярны и лежат на биссектрисах его углов.

Доказательство.

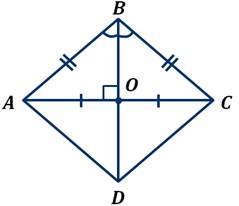
Рассмотрим .

, следовательно,  – медиана.

.

 – равнобедренный.

Медиана – биссектриса, высота.

Следовательно, диагональ  и лежит на биссектрисе  .

Что и требовалось доказать.

Теперь сформулируем и докажем признаки ромба.

Теорема. Признак ромба. Если у параллелограмма диагонали взаимно перпендикулярны, то этот параллелограмм – ромб.

Доказательство.

Рассмотрим  и .

Сторона  – общая, , так как диагонали  т.  делятся пополам

 по двум катетам.

Следовательно, .

, .

Следовательно, .

 – ромб.

Что и требовалось доказать.

И ещё один признак.

Теорема. Признак ромба. Если у параллелограмма одна из диагоналей лежит на биссектрисе угла, то этот параллелограмм – ромб.

Доказательство.

.

как накр. лежащие при и секущей .

Следовательно, .

 – равнобедренный, то есть .

,.

Следовательно, .

 – ромб.

Что и требовалось доказать.

Задача. Чему равны углы ромба, если его меньшая диагональ равна стороне?

Решение.

 – равносторонний.

.

,

.

Ответ: , , , .

Решим ещё одну задачу.

Задача. В ромбе  перпендикуляр , проведённый из вершины  делит сторону  пополам. Найдите градусную меру .

Решение.

 – прямоугольный.

.

, то есть  .

.

, – внутр. одностор. при   и секущей .

.

Так как , то .

.

.

Ответ: .

Теперь поговорим о квадрате.

Квадрат – это прямоугольник, у которого все стороны равны. Также можно сказать, что квадрат – это ромб, у которого все углы прямые.

Эти два определения равносильны. Из каждого следует, что квадрат – это  параллелограмм, который одновременно является и прямоугольником, и ромбом.

Следовательно, квадрат обладает всеми свойствами и прямоугольника, и ромба.

Основные свойства квадрата:

1.Все углы квадрата прямые.

2. Диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и лежат на биссектрисах его углов.

Задача. На рисунке  – квадрат, . Найдите .

Решение.

.

,  – смежные, то есть  .

Так как , то .

.

 – равнобедренный, тогда .

,

,

,

.

,,

то есть ,.

Ответ: ,.