Вопросы занятия:
· повторить, как извлекается корень n-ой степени из числа;
· повторить свойства арифметического корня n-ой степени;
· показать, как можно применить свойства корня при решении задач.
Материал урока
Определение.
Корнем n-ой степени из числа а называется такое число, энная степень которого равна А.
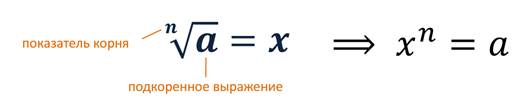
Говоря о корне энной степени нужно понимать, что показатель корня n является натуральным числом.
Вам хорошо известен такой частный случай корня n-ой степени, как корень второй степени, то есть квадратный корень из числа. Показатель корня в этом случае не пишут.
Определение.
Квадратным корнем из числа называют такое число, квадрат которого равен числу а.

Например,

Ещё одним частным случаем является корень третьей степени, мы привыкли называть его корнем кубическим.
Например,

Вы могли задаться вопросом, почему.

Чтобы ответить на этот вопрос, рассмотрим два случая корня энной степени: где показатель корня является нечётным числом и где показатель корня является чётным числом.


Но чтобы избавиться от неоднозначности в вычислениях, договорились неотрицательный корень n-ой степени обозначать как «корень n-ой степени из а». А отрицательный как «минус корень n-ой степени из а».

Исходя из этой договорённости и становится понятно, что

Из рассмотренных случаев можем сделать заключение, что:

Пример.

Вернёмся к определению корня энной степени

В первую запись вместо можно подставить:

Тогда получаем свойство, которым очень удобно пользоваться при вычислении корня энной степени.
Но ведь корень чётной степени мы договорились считать числом неотрицательным. Поэтому чтобы не возникало путаницы при вычислении корней, вместо этого свойства мы пользовались двумя:
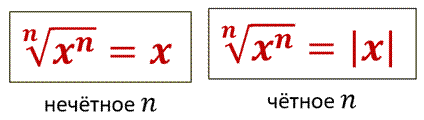
Пример.

Вы видите, что корень энной степени из любого неотрицательного числа а имеет смысл при любых Эн и принимает неотрицательные значения. Такой корень называют арифметическим корнем n-ой степени из числа а.
Любой корень можно выразить через арифметический.
Корни чётных степеней всегда являются арифметическими, ведь подкоренное выражение у них является числом неотрицательным, и под их значениями мы условились понимать неотрицательные числа.
Это же касается корней нечётных степеней из неотрицательных чисел.
А вот, например, корни нечётных степеней из отрицательных чисел можно записать так, при этом вынеся минус перед корнем.

Таким образом, при работе с любым корнем энной степени можно всегда перейти к рассмотрению арифметического корня.
Также при работе с корнями энной степени очень важно знать ещё несколько свойств. Напомним их.

Все эти свойства пригодятся вам при работе с выражениями, содержащими знак корня.
Итоги урока
На этом уроке мы с вами вспомнили, как извлекать корень n-ой степени из числа. Напомнили, что корень n-ой степени из неотрицательного числа считают числом неотрицательным, и называют «арифметическим корнем n-ой степени».
Так корень чётной степени из неотрицательного числа всегда является корнем арифметическим и поэтому равен числу неотрицательному. А корня чётной степени из отрицательного числа не существует. Корень нечётной степени из неотрицательного числа равен числу неотрицательному. Например, корень третьей степени из двадцати семи равен трём.
Ну, а корень нечётной степени из отрицательного числа равен числу отрицательному. Его нужно выражать с помощью арифметического корня n-ой степени, при этом вынося минус из-под знака корня. Также мы напомнили свойства арифметического корня энной степени и применили их на конкретных примерах.



 Получите свидетельство
Получите свидетельство Вход
Вход



 0
0 14513
14513

