Графические информационные модели. Использование графов при решении задач

Вопросы:

·      Решение задач с помощью графов.

·      Что такое граф?

·      Какие виды графов бывают и чем они отличаются?

Граф – это совокупность объектов со связями между ними. Вершины – это объекты, а ребра – это связи.

Взвешенный граф – это граф, в котором вершины или рёбра характеризуются некоторой дополнительной информацией – весами вершин или рёбер.

Цепь – это путь по вершинам и рёбрам графа, в который любое ребро графа входит не более одного раза.

Цикл – это цепь, в которой начальная и конечная вершины совпадают.

Сеть – это граф с циклом.

Семантическая сеть – это информационная модель, имеющая вид графа, вершинам которого соответствуют определённые объекты, а рёбра задают отношения между ними.

Дерево – это граф, в котором нет циклов, то есть в нём нельзя из некоторой вершины пройти по различным рёбрам и вернуться в ту же вершину.

А теперь приступим к решению задач с использованием графов.

Задача 1: У Маши есть 2 конверта: обычный и экспресс, и 3 марки: круглая, прямоугольная и треугольная. Сколькими способами Маша может выбрать конверт и марку, чтобы отправить письмо?

Нарисуем граф. Первую вершину графа обозначим буквой П – письмо. От письма будут отходить два ребра к вершине О (обычный) и Э (экспресс). От каждой вершины О и Э будут отходить по три ребра к каждому виду марки, которые обозначим соответственно буквами К – круглая, П – прямоугольная и Т – треугольная. Сосчитав получившиеся вершины, мы можем ответить на поставленный вопрос.

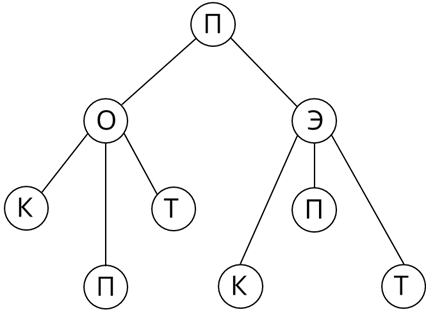
Ответ: Маша может выбрать конверт и марку шестью разными способами.

Задача 2: На дополнительное занятие по физической культуре пришли восемь учащихся: Саша, Маша, Таня, Артём, Женя, Лёша, Настя и Юра. Физкультурный руководитель Николай Владимирович попросил их построиться по росту. Известно, что Саша выше Маши, Таня выше Артёма, Женя ниже Лёши, но выше Насти, Настя выше Саши, Лёша ниже Юры, а Маша выше Тани. Давайте поможем ребятам выстроиться по росту.

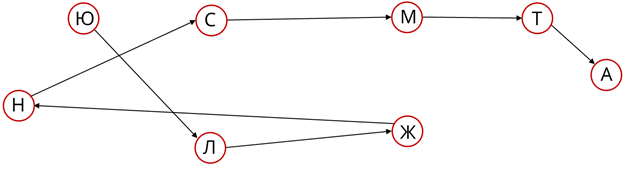
Для этого будем использовать граф. Вершинами нашего графа будут первые буквы имён ребят. В задаче мы видим, что существует две категории определения роста: «быть выше» и «быть ниже». Рассмотрим категорию «быть выше» и проведём стрелки от более высокого учащегося к более низкому. В задаче сказано, что Саша выше Маши, соответственно стрелку проводим от Саши к Маше. Таким же образом проставляем стрелки от Тани к Артёму. Так как по условию задачи Женя ниже Лёши, соответственно Лёша будет выше Жени, значит проведём стрелку от Лёши к Жене, затем от Жени к Насте и так далее. В результате получим граф.

Найдём на нём ученика, к которому не идёт ни одной стрелки. Это Юра. Значит он будет самым высоким среди всех. Далее идём по стрелке от Юры к Лёше, это говорит о том, что Лёша будет стоять на втором месте. Далее идёт Женя, Настя, Саша, Маша, Таня и Артём. Таким образом мы помогли учащимся выстроиться по росту.

Задача 3: Крестьянин купил на базаре козу, кочан капусты и волка. По дороге домой нужно было переправиться через реку. У крестьянина была маленькая лодка, в которую кроме него могла поместиться только одна из его покупок.

Как ему переправить все товары через реку, если нельзя оставлять козу наедине с капустой и волка наедине с козой?

Решим задачу с использованием графов. Итак, изначально на берегу находятся крестьянин, волк, коза и капуста. Проведём первое ребро, когда крестьянин переправится один.

Этого делать нельзя, так как коза может съесть капусту или же волк съест козу. Рассмотрим следующий вариант: Крестьянин перевезёт волка через реку, а на берегу останется коза с капустой.

Такой вариант нам тоже не подходит. А если попробовать переправить через реку козу, а волка оставить с капустой?

Волк не съест капусту, значит, данный вариант нам подходит. Выделим его на нашем графе. Ну и рассмотрим ещё один вариант, крестьянин переправит капусту, а на берегу останется волк с козой.

Такой вариант не подходит. Теперь вернёмся к выделенному варианту. На первом берегу у нас остались волк и капуста, а на втором берегу крестьянин и коза. Крестьянин соответственно вернётся к волку и капусте.

Здесь так же есть два варианта переправы.

Рассмотрим первый из них. Можно на берегу оставить капусту и перевезти волка. На втором берегу у нас окажутся крестьянин, коза и волк. Далее крестьянин может отправиться за капустой и оставить на втором берегу козу и волка.

Но этот вариант нам не подходит. Есть ещё один: крестьянин забирает козу и переправляет её к капусте. Соответственно на первом берегу у нас окажутся крестьянин, капуста и коза, а на втором – волк. В данном случае есть два варианта переправы. Первый: оставить козу с капустой и отправится к волку, но данный вариант нам не подходит.

Второй: перевезти капусту к волку. И крестьянину останется вернуться за козой и переправить её на второй берег.

В данной ветви графа мы рассмотрели первый путь переправы.

Переходим ко второму. Для этого вернёмся к вершине графа, где на первом берегу остались крестьянин, волк и капуста, а на втором – коза. Так как в первом случае крестьянин перевозил волка, теперь возьмём капусту и переправим к козе. Таким образом, на первом берегу останется волк, а на втором крестьянин, коза и капуста.

Крестьянину нужно вернуться за волком, но он не может оставить козу с капустой, поэтому этот вариант не подходит. Крестьянину нужно взять козу и перевести к волку.

Таким образом на первом берегу у нас будут волк, коза и крестьянин, а на втором – капуста. Здесь существует два варианта. Крестьянин может один переправиться к капусте, что естественно будет неправильно, или же взять волка и перевезти на второй берег.

Таким образом получим, что на первом берегу у нас осталась коза, а на втором крестьянин, волк и капуста.

Обратите внимание, что мы пришли к такому же варианту, как и в первом случае. Далее переправа будет в той же последовательности, как и в первой ситуации. Крестьянину останется перевезти капусту к волку. И затем вернуться за козой и переправить её на второй берег.

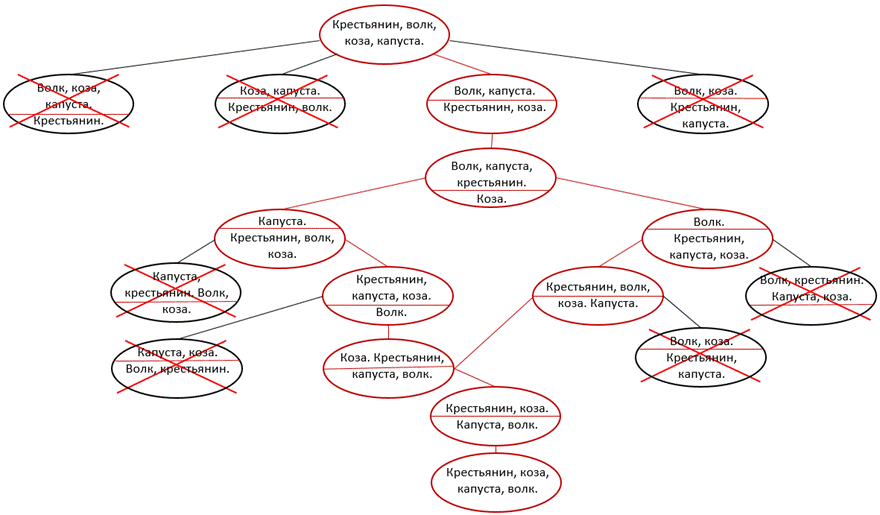
Заметим, что если сосчитать количество переправ с одного берега на другой и обратно, то мы во всех случаях получим по семь раз, по какой бы ветви графа мы не пошли.

Задача 4: Сколько трёхзначных чисел можно составить из четырёх цифр: 1, 2, 3 и 4.

Для начала решим эту задачу с использованием графов. Нам понадобится четыре графа, корневыми вершинами которых будут числа один, два, три и четыре соответственно. Эти вершины будут обозначать разряд сотен. Рассмотрим решение данной задачи на примере графа с корневой вершиной один. От этой вершины будут отходить четыре ребра к вершинам с цифрами один, два, три и четыре, которые будут обозначать разряд десятков. И от каждого десятка будут отходить четыре ребра к разрядам единиц. Получим следующий граф.

Три остальных графа будут аналогичны первому, с одним лишь отличием – корневой вершиной.

Для того чтобы узнать количество трёхзначных чисел, состоящих из цифр один, два, три и четыре можно сосчитать сколько получилось вариантов в разряде единиц каждого числа. Вы видите, что вариантов много и для того, чтобы не пересчитывать количество, можно воспользоваться комбинаторным правилом умножения:

Пусть имеется n элементов и требуется выбрать из них один за другим k элементов.

Если первый элемент можно выбрать n₁ способами, после чего второй элемент можно выбрать n₂ способами из оставшихся, затем третий элемент можно выбрать n₃ способами из оставшихся и так далее, то число способов, которыми могут быть выбраны k элементов, равно:

n₁×n₂×n₃×…×n_k

Итак, у нас четыре элемента, значит n равно четырём. Количество цифр в трёхзначном числе 3, тогда k равно трём. Первую цифру можно выбрать четырьмя способами, вторую и третью также четырьмя способами, так как условием задачи не запрещено повторять цифры в числе. В результате мы получаем, что из цифр 1, 2, 3 и 4 можно составить 64 различных трёхзначных числа.

Как видите, не всегда нужно строить граф. Чаще всего его используют, если нужно записать или же выбрать определённые числа, состоящие из этих цифр.

Сегодня мы вспомнили: термины с прошлого урока: граф, взвешенный граф, цепь, цикл, сеть, семантическая сеть и дерево.

C помощью графов научились решать некоторые задачи: находить количество всех возможных комбинаций и выбирать из всех вариантов решения те, которые подходят по условию.