Напряженность электрического поля. Принцип суперпозиции полей

Напомним, что не так давно мы познакомились с понятием электрического поля. Электрическое поле — это особая форма материи, которая создается покоящимися электрическими зарядами и оказывает воздействие на другие заряды.

Для того, чтобы каким-то образом описать электрическое поле, необходимо ввести количественную характеристику, которая называется напряженностью электрического поля. Рассмотрим электрическое поле, создаваемое зарядом q₁. Мы можем помещать в разные точки этого поля заряд q₂ и измерять силу, с которой поле заряда q₁ действует на заряд q₂.

Исходя из закона Кулона:

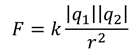
Таким образом, отношение силы, действующей на заряд со стороны поля, к величине этого заряда не зависит от самого заряда:

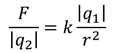
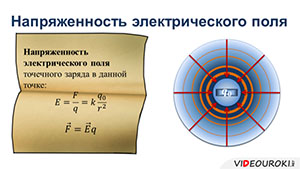
Поэтому, можно считать это отношение характеристикой поля. Итак, напряженность электрического поля — это отношение силы, действующей на помещаемый в данную точку поля заряд, к величине этого заряда:

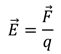
Как видно из формулы, единицей измерения напряженности поля является ньютон на кулон:

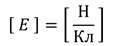
Напряженность электрического поля, как и сила, является векторной величиной.

Направление вектора напряженности совпадает с направлением вектора силы, действующей на положительный заряд, помещенный в данное поле.

Исходя из всего выше сказанного, мы можем найти напряженность электрического поля, созданного точечным зарядом:

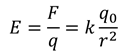
Как видно из формулы, напряженность поля в данной точке прямо пропорциональна величине заряда и обратно пропорциональна квадрату расстояния между зарядом и данной точкой поля.

Рассмотрим простой пример, когда точечный положительный заряд создает электростатическое поле.

Модуль напряженности данного поля вычисляется по формуле, которую мы только что рассматривали. То есть напряженность будет убывать пропорционально квадрату расстояния между зарядом и данной точкой поля. Таким образом, во множестве точек, равноудаленных от заряда будет наблюдаться одинаковая напряженность. Как вы знаете, множество точек равноудаленных от центра — это есть ни что иное, как сфера.

Теперь, внесем в данное поле так называемый пробный заряд. Пробным зарядом называется точечный положительный заряд.

Как вы знаете, в данном случае возникнет кулоновская сила отталкивания:

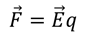
Исходя из этого, мы можем определить направление вектора напряженности. Таким образом, мы можем заключить, что вектор напряженности будет направлен вдоль прямой, соединяющей заряд и данную точку поля.

Теперь внесем пробный заряд в поле, создаваемое отрицательным зарядом. В этом случае между отрицательным зарядом и пробным зарядом возникнет кулоновская сила притяжения. Поскольку напряженность сонаправлена с силой Кулона, мы можем заключить, что напряженность поля, создаваемого отрицательным зарядом, будет направлена не от заряда, а к заряду.

Возникает резонный вопрос: как охарактеризовать поле, если оно создается не одним, а несколькими зарядами? В этом случае, нам снова нужно воспользоваться пробным зарядом и рассмотреть, силы, действующие на него:

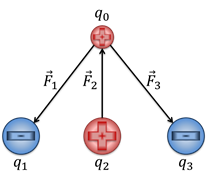
Итак, на рисунке пробный заряд обозначен за q₀. На него будут действовать кулоновские силы притяжения со стороны зарядов q₁ и q₃ (поскольку они отрицательные) и кулоновская сила отталкивания со стороны заряда q₂ (поскольку он положительный). Как вы знаете, результирующая сила равна векторной сумме всех сил, действующих на данное тело:

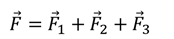
Если теперь мы разделим это уравнение на величину пробного заряда, то получим, что напряженность поля в данной точке равна векторной сумме напряженностей полей, создаваемых зарядами:

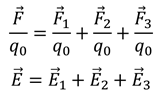
Этот метод называется принципом суперпозиции полей, который гласит следующее: если в данной точке пространства различные заряженные частицы создают электрические поля, с определенными напряженностями, то результирующая напряженность поля в этой точке будет равна векторной сумме напряженностей этих полей.

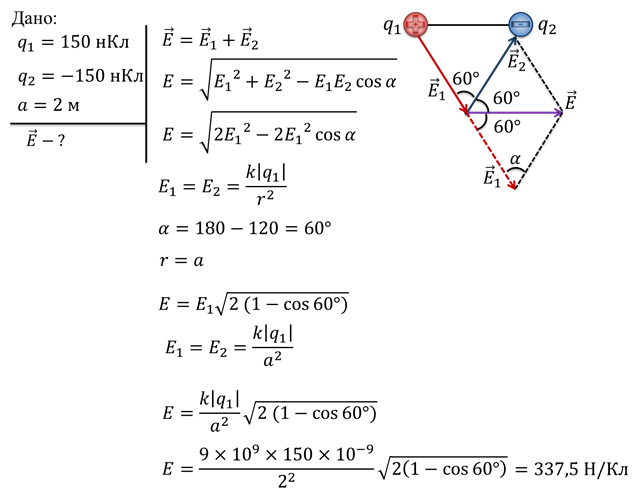
Пример решения задачи.

Задача. Два равных по модулю заряда находятся в вершинах равностороннего треугольника, сторона которого равна 2 м. Найдите модуль и направление напряженности в третьей вершине треугольника, если модуль заряда равен 150 нКл.