Наибольший общий делитель. Взаимно простые числа

На данном уроке мы продолжим работу с делителями числа. Напомним, что делителем натурального числа а называют натуральное число, на которое а делится без остатка.

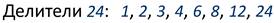
Рассмотрим простой случай. Саша и Маша решили украсить кабинет осенними букетами из сухих листьев. Саша собрал 12 кленовых листьев. Маша принесла 18 листьев каштана.

«А как нам узнать, какое количество букетов мы сможем составить, чтобы в каждом клиновых листьев было одинаковое количество, да и листьев каштана во всех букетах было поровну?» – спросил Саша.

«Каждое из чисел 12 и 18 должно делиться на число букетов» – ответила Маша. – «Поэтому выпишем все делители этих чисел».

Попробуем перевести эту задачу на математический язык.

Определение

Наибольшее натуральное число, на которое делятся без остатка числа a и b, называют наибольшим общим делителем этих чисел.

Наибольший общий делитель двух чисел обозначается НОД (по первым буквам слов «Наибольший Общий Делитель»).

Например

Наибольший общий делитель чисел 12 и 18 равен 6.

Теперь найдём НОД чисел 26 и 45.

Определение

Обратите внимание, что существуют числа, у которых только один общий делитель: единица. Такие числа называют взаимно простыми.

Таким образом, числа называются взаимно простыми, если у них нет общих делителей кроме единицы.

НОД взаимно простых чисел равен 1.

Чтобы находить наибольший общий делитель, не обязательно перебирать все делители чисел. В некоторых случаях это очень долгая и кропотливая работа. Существует другой способ.

Чтобы найти наибольший общий делитель двух чисел надо: разложить каждое из чисел на простые множители.

Примеры

Задание

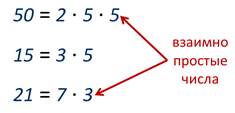
Обратите внимание, как интересно получается: сами числа составные, а вот между собой – взаимно простые.

Итоги

Наибольшее натуральное число, на которое делятся без остатка числа a и b, называют наибольшим общим делителем этих чисел.

Наибольший общий делитель двух чисел обозначается НОД по первым буквам слов «Наибольший Общий Делитель».

Если у нескольких чисел нет общих делителей кроме единицы, то эти числа называются взаимно простыми. НОД взаимно простых чисел равен 1.