«То, что мы знаем, – ограничено,
а то, чего мы не знаем, – бесконечно»
Пьер-Симон Лаплас
Данная тема посвящена решению задач на конденсаторы.
Задача 1. Найдите электроёмкость конденсатора, который при зарядке до напряжения 1,5 кВ, получает заряд, равный 60 мкКл.
|
ДАНО:
|
СИ
|
РЕШЕНИЕ Запишем формулу, по которой рассчитывается электроёмкость
Тогда получаем, что при условиях задача она равна
|
|
|
Ответ: 40 нФ.
Задача 2. На первый конденсатор подаётся напряжение 100 В, а на второй — 250 В. При этом, конденсаторы накапливают одинаковые заряды. Сравните электроёмкости этих конденсаторов.
|
ДАНО:
|
РЕШЕНИЕ Запишем формулу для вычисления электроёмкости
Тогда электроёмкости первого и второго конденсаторов равны
Т.к. заряды равны, то отношение электроёмкостей обратно пропорционально отношению напряжений
|
|
|
Ответ: электроёмкость первого конденсатора в 2,5 раза больше, чем электроёмкость второго конденсатора.
Задача 3. Плоский конденсатор, в котором в качестве диэлектрика используется бумага, имеет электроёмкость 20 нФ. Расстояние между пластинами конденсатора равно 0,4 мм. Если при напряжении 500 В, конденсатор обладает потенциальной энергией 12 мкДж, то какова площадь одной пластины этого конденсатора?
|
ДАНО:
|
СИ
|
РЕШЕНИЕ
Запишем формулу для определения электроёмкости плоского конденсатора
Потенциальная энергия заряженного конденсатора равна
Подставляя первую формулу во вторую получим
|
|
|
Ответ: 17 см2.
Задача 4. На пластинах плоского бумажного конденсатора равномерно распределен заряд с поверхностной плотностью 600 нКл/м2. Расстояние между пластинами равно 0,5 мм. Как изменится напряжение между его обкладками при увеличении расстояния между пластинами до 2 мм?
|
ДАНО:
|
СИ
|
РЕШЕНИЕ
Запишем формулу для расчета электроёмкости плоского конденсатора
Электроёмкость в общем виде может быть выражена по формуле
Поверхностная плотность заряда определяется по выражению
Приравняем первые две формулы
Исходя из формулы для определения поверхностной плотности, величина заряда равна
Тогда
|
|
|
Ответ: напряжение увеличится на 40,7 В.
Задача 5. При увеличении напряжения, поданного на конденсатор с ёмкостью 6 мкФ, в 3 раза, энергия поля возросла на 0,2 Дж. Найдите заряд на конденсаторе до увеличения напряжения.
|
ДАНО:
|
СИ
|
РЕШЕНИЕ Запишем формулу, по которой вычисляется потенциальная энергия заряженного конденсатора
Запишем общую формулу для определения электроёмкости конденсатора
Запишем теперь выражения для начальной и конечной энергии конденсатора
Разность этих энергий равна
В условии задачи сказано, что
С учетом последнего равенства получаем
Из общего определения электроёмкости
Тогда
|
|
|
Ответ: 2,2 мКл.

 Получите свидетельство
Получите свидетельство Вход
Вход







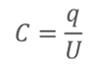
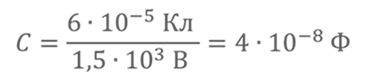





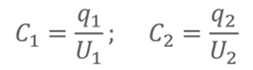
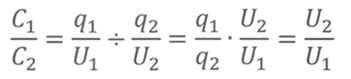
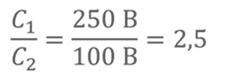
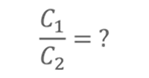


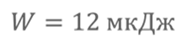






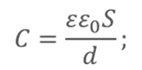
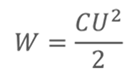

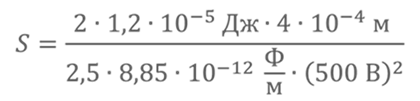




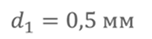


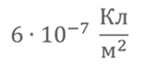



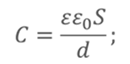

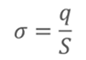
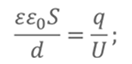









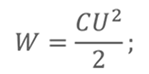








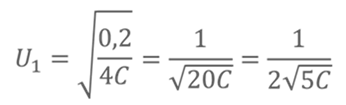
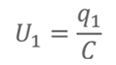

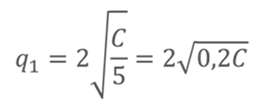


 0
0 10248
10248


