На этом уроке мы познакомимся с понятием конуса. Дадим определение конуса. Рассмотрим, какими элементами он обладает. А также разберемся, как находят объем, площадь боковой поверхности и площадь полной поверхности конуса.
Итак, рассмотрим понятие конуса. Вокруг нас существует множество предметов, имеющих форму конуса. Вафельные рожки для мороженного имеют форму конуса, дорожный конус, шляпа ведьмочки для хэлоуина, колпак у Буратино, колпаки для дня рождения, некоторые архитектурные сооружения, декоративным растениям, придают форму конуса и многое другое.

Конус – это один из видов тел вращения. Итак, если взять прямоугольный треугольник, например, треугольник ABC и вращать его вокруг катета AB, то в результате получится тело, которое называется конусом.
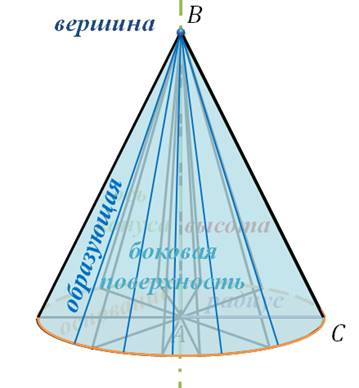
Прямая AB называется осью конуса. А отрезок AB – его высотой.
При вращении катета AC образуется круг, он называется основанием конуса.
Иногда радиус этого круга называют радиусом конуса.
При вращении гипотенузы BC образуется поверхность, состоящая из отрезков с общим концом B. Ее называют конической поверхностью или боковой поверхностью конуса.
Отрезки, из которых она составлена, называются образующими конуса.
Точка B называется вершиной конуса.
Определение. Конус – это тело, ограниченное кругом и конической поверхностью.
Пользуясь принципом Кавальери, можно доказать, что объем конуса
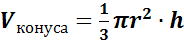 , где r –
радиус основания конуса, h – его высота.
, где r –
радиус основания конуса, h – его высота.
На рисунке изображен конус, у которого радиус равен r, а образующая равна l. Боковую поверхность конуса, как и боковую поверхность цилиндра, можно развернуть на плоскость, разрезав ее по одной из образующих.
Давайте представим, что боковую поверхность конуса разрезали по образующей AB и развернули таким образом, что получился круговой сектор ABB’. Стороны AB и A’B которого являются двумя краями разреза боковой поверхности конуса.
Разверткой боковой поверхности конуса является круговой сектор. Обратите внимание, радиус сектора равен образующей конуса, т.е. l. А длина дуги сектора равна длине окружности основания конуса, т.е. равна 2πr.
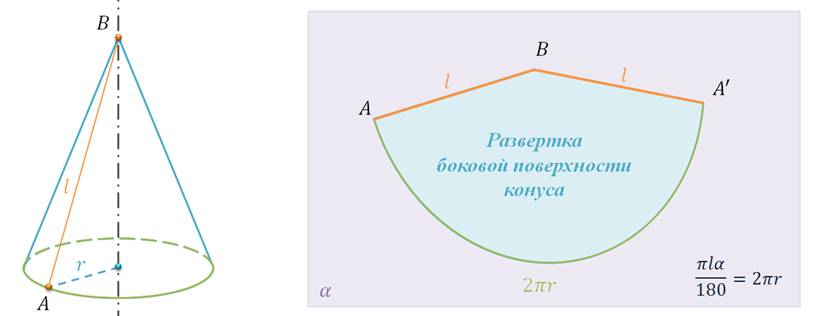
За площадь боковой поверхности конуса принимается площадь ее развертки. Выразим площадь боковой поверхности конуса через его образующую l и радиус основания r.
Площадь кругового сектора – развертки боковой поверхности конуса –
равна 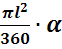 , где α – градусная мера дуги
сектора.
, где α – градусная мера дуги
сектора.
Длина дуги окружности с градусной мерой α и радиусом l равна пи эль альфа деленное на сто восемьдесят. С другой
стороны, длина этой дуги равна два пи эр, т.е. 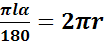 . Отсюда, площадь боковой поверхности
конуса
. Отсюда, площадь боковой поверхности
конуса
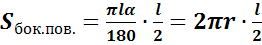 . Т.е. площадь боковой поверхности
конуса с образующей l и радиусом основания r выражается формулой:
. Т.е. площадь боковой поверхности
конуса с образующей l и радиусом основания r выражается формулой:  .
.
Площадью полной поверхности конуса называется сумма площадей боковой
поверхности и основания. Отсюда видим,
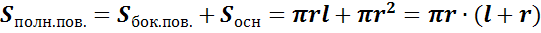 .
.
Задача. Радиус основы конуса 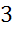 метра,
высота
метра,
высота  метра. Найдите площади боковой и
полной поверхностей конуса.
метра. Найдите площади боковой и
полной поверхностей конуса.
Решение.
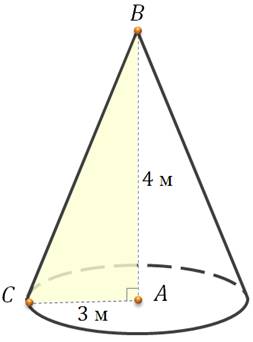
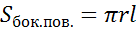

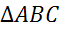 – прямоугольный.
– прямоугольный.
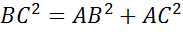
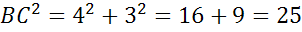
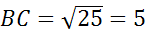 (м)
(м)
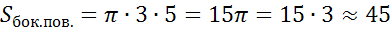 (м2)
(м2)
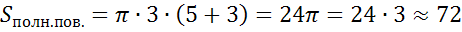 (м2)
(м2)
Ответ: 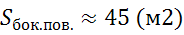 ,
, 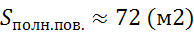 .
.
Задача. Радиус основы конуса 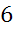 см,
высота
см,
высота 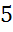 см. Найдите объем конуса,
см. Найдите объем конуса, 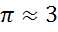 .
.
Решение.
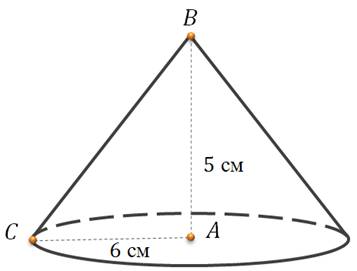
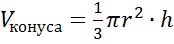
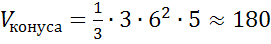 (см3)
(см3)
Ответ:  .
.
Конус в переводе с греческого «konos» означает «сосновая шишка». С конусом люди знакомы с глубокой древности. В 1906 году была обнаружена книга «О методе», написанная Архимедом. В этой книге дается решение задачи об объеме общей части пересекающихся цилиндров. Архимед приписывает честь открытия этого принципа древнегреческому философу Демокриту. С помощью этого принципа Демокрит получил формулы для вычисления объема пирамиды и конуса.
Подведем итоги. На этом уроке мы познакомились с понятием конуса. Узнали, что конус – это тело, ограниченное кругом и конической поверхностью. Рассмотрели, какими элементами он обладает. А также разобрались, как находят объем, площадь боковой поверхности и площадь полной поверхности конуса.

 Получите свидетельство
Получите свидетельство Вход
Вход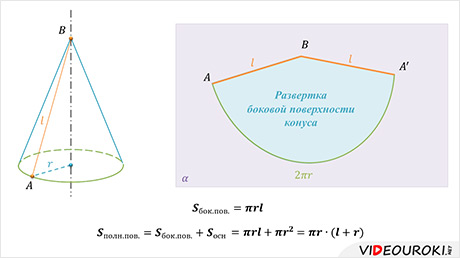



 0
0 6523
6523



