“Умение решать задачи — это практическое
искусство, подобное плаванию или катанию
на лыжах, или игре на фортепиано: научиться
этому можно, лишь подражая избранным
образцам и постоянно тренируясь”
Д. Пойа
На предыдущих темах повторялись основные понятия, связанные с магнитным полем.
Магнитное поле — это особый вид материи, посредством которого осуществляется взаимодействие между движущимися электрически заряженными частицами.
Силовой характеристикой магнитного поля является магнитная индукция — векторная величина, являющаяся силовой характеристикой магнитного поля и которая полностью характеризует магнитное поле.
В магнитном поле на проводник с током действует сила Ампера, а на отдельно движущуюся частицу — сила Лоренца.
В данной теме рассмотрим основные типы задач, а также попытаемся выделить общую методику их решений. В представленной теме можно выделить три типа задач:
1) на расчет полей (вычисление магнитной индукции, в какой либо точке магнитного поля);
2) о силовом действии магнитного поля на проводники или контур с током;
3) о силовом действии магнитного поля на движущиеся в нем заряженные частицы.
Рассмотрим первый тип задач на конкретных примерах.
Задача 1. По четырем длинным прямым параллельным проводникам, проходящим через вершины квадрата, со стороной 30 см, перпендикулярно его плоскости, проходят одинаковые токи по 10 А, причем по трем проводникам проходят токи в одном направлении, а по четвертому — в противоположном. Определите индукцию магнитного поля в центре квадрата.

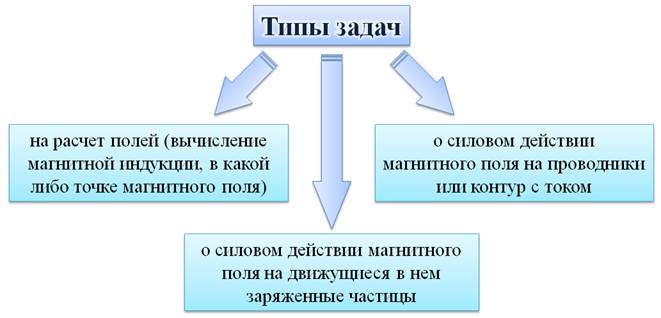
Задача 2. Соленоид длиной 40 см и диаметром 4 см, содержит 2000 витков проволоки сопротивлением 150 Ом. Определите индукцию магнитного поля внутри катушки, если к ней подведено напряжение 6 В.
Выделим общие рекомендации для решения задач на расчет полей. При решении задач данного типа, главное следует помнить, что силовой характеристикой магнитного поля является магнитная индукция, которая в каждой точке поля направлена по касательной к линии магнитной индукции. Поэтому необходимо:
1. Сделать схематический рисунок, указав на нем проводник с током, создающий магнитное поле;
2. Через данную точку провести линию магнитной индукции, определив ее направление, пользуясь правилом правого винта;
3. Изобразить магнитную индукцию в точке наблюдения вектора индукции магнитного поля, направленную по касательной к линии магнитной индукции;
4. Рассчитать модуль магнитной индукции, используя формулы для магнитного поля;
5. При нахождении магнитной индукции поля, созданного несколькими токами, следует использовать принцип суперпозиции полей, при этом обязательно нужно помнить, что это векторная сумма.
Рассмотрим пример задачи второго типа, т.е. задачи на силовое действие магнитного поля на проводник с током.
Задача 3. Прямой проводник длиной 0,2 м и массой 5 г подвешен горизонтально на двух невесомых нитях в однородном магнитном поле. Вектор магнитной индукции перпендикулярен проводнику и равен по модулю 49 мТл. Какой ток надо пропустить через проводник, чтобы одна из нитей разорвалась, если нить разрывается при нагрузке, равной или превышающей 39,2 мН?

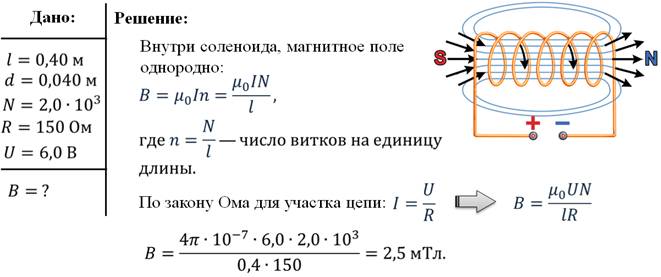
Задача 4. Определите силу взаимодействия, приходящуюся на единицу длины проводов воздушной линии электропередач, если сила тока в линии составляет 500 А, а расстояние между проводами 50 см.
Выделим основные этапы, необходимые для решения задач подобного типа:
1. Сделать схематический чертеж, указав на нем линии индукции магнитного поля. Часто линии индукции изображают в плоскости чертежа, в некоторых случаях удобно их изображать перпендикулярно плоскости;
2. Изобразить контур с током, находящийся в этом поле. Отметить углы между направлением поля и отдельными элементами контура, если последний состоит из нескольких прямых проводников;
3. Используя правило левой руки, определить направление сил Ампера, действующих на каждый элемент контура, и изобразить их на чертеже;
4. Записать формулы для сил Ампера или вращающего момента, создаваемого этими силами и найти из них искомую величину;
5. Если в задаче рассматривается равновесие проводника или его движение в магнитном поле, то, кроме силы Ампера, нужно указать и все остальные силы, действующие на проводник, и записать условия его равновесия или основное уравнение динамики, спроецировав векторные величины на оси Х и У, найти искомую величину.
Рассмотрим третий тип задач: о силовом действии магнитного поля на движущиеся в нем заряженные частицы.
Задача 5. Протон влетает в однородное магнитное поле со скоростью 1000 м/с под углом 600 к линиям магнитной индукции. Определите радиус и шаг винтовой линии, по которой будет двигаться протон, если магнитная индукция поля равна 10 мТл.


Выделим общие этапы решения задач данного типа. При решении задач о силовом действие магнитного поля на движущиеся в нем заряженные частицы необходимо:
1) Сделать чертеж, указав на нем линии индукции магнитного поля, начальную скорость частицы и отметить знак ее заряда;
2) Если скорость частицы направлена под углом к линии индукции магнитного поля, ее следует разложить на две составляющие, одна из которых должна быть перпендикулярна магнитной индукции, вторая параллельна ей. Такое разложение позволяет представить сложное движение в виде двух более простых и в значительной мере упрощает задачу, поскольку при движении частицы вдоль линии магнитного поля сила Лоренца на частицу не действует;
3) Изобразить силы, действующие на заряженную частицу. При нахождении направления силы Лоренца по правилу левой руки следует обратить особое внимание на знак заряда частицы;
4) Указав силы, нужно попытаться определить вид траектории частицы;
5) записать основное уравнение динамики, выбрать оси координат и спроецировать векторные величины на оси х и у;
6) используя формулу силы Лоренца, подставить в полученные уравнения значения сил, добавить при необходимости к уравнениям динамики еще формулы кинематики и решить полученную систему уравнении относительно искомой величины.

 Получите свидетельство
Получите свидетельство Вход
Вход




 0
0 42739
42739

