Расчёт сопротивления проводника. Удельное сопротивление. Примеры расчетов

Сопротивление в проводниках возникает из-за взаимодействия электронов с ионами кристаллической решетки. Если вдуматься, то можно заметить, что чем длиннее проводник, тем больше такое взаимодействие.

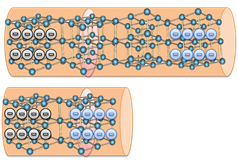
Также, логично предположить, что чем толще проводник, тем больший поток электронов может пройти через поперечное сечение.

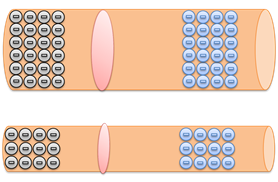
И, конечно, мы знаем, что разные вещества по-разному проводят ток. Исходя из этих знаний, мы можем установить следующее:

Чем длиннее проводник, тем больше его сопротивление.

Чем толще проводник, тем меньше его сопротивление.

Сопротивления проводников одинаковой длины и толщины могут быть различны, в зависимости от вещества.

Ну а как именно зависит сопротивление проводника от его размеров, можно узнать только с помощью опытов. Мы уже немного знакомы с методикой проведения подобных экспериментов: нам нужно провести некоторые измерения, и, построив график, установить зависимость сопротивления от тех или иных величин. Данные опыты были проведены Георгом Омом.

Подключим проводник к источнику тока и, с помощью амперметра и вольтметра, измерим силу тока и напряжение. Мы используем, так называемый, мультиметр — современный прибор, который выполняет функции амперметра и вольтметра, в зависимости от настроек. Но, тем не менее, мы по-прежнему должны следовать правилам: когда мы хотим измерить силу тока, мультиметр подключается последовательно. На мультиметре есть переключатель между режимами измерения той или иной величины. Также, когда мы хотим измерить напряжение, мультиметр подключается параллельно. Используя закон Ома, мы можем вычислить сопротивление данного проводника.

Подобным способом, мы можем вычислить сопротивление проводников разной длины, но той же толщины, сделанных из того же материала. Проведя несколько измерений, выясним, что сопротивление проводника увеличивается ровно во столько раз, во сколько увеличивается его длина.

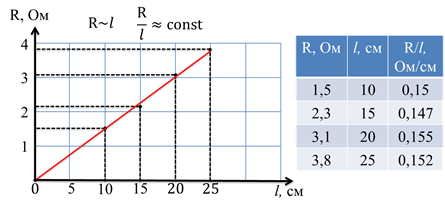
В таблице с данными можно увидеть незначительные несоответствия. Однако, мелкие погрешности в измерениях, при проведении любого опыта, неизбежны. Тем не менее, закономерность очевидна: сопротивление проводника прямо пропорционально длине проводника. Это подтверждается и графиком, который является прямой линией.

Проведем несколько иной опыт: сравним сопротивления проводников из того же материала, одинаковой длины, но разной толщины. Поскольку роль играет не сама толщина, а площадь поперечного сечения проводника, то мы попытаемся выяснять, как зависит сопротивление именно от этого параметра.

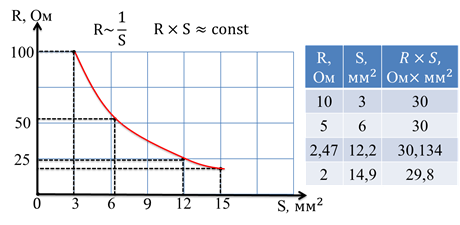
Полученные данные показывают, что на этот раз сопротивление проводника обратно пропорционально площади поперечного сечения проводника. Наш график зависимости сопротивления от поперечного сечения имеет форму ветви гиперболы.

Как вы уже, наверное, догадались, удельное сопротивление проводников из того или иного материала тоже вычисляется экспериментальным путём. На этот раз, все проводники имеют одну и ту же длину и толщину, но состоят из разного вещества.

Удельное сопротивление проводника — это сопротивление проводника из данного вещества с площадью поперечного сечения 1 м² и длиной 1 м. В таблице даны значения удельного сопротивления для некоторых веществ.  

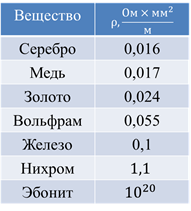
Однако, площадь поперечного сечения проводника удобнее измерять в квадратных миллиметрах, поскольку это больше соответствует размерам реальных проводников.

Итак, исходя из наших опытов, сопротивление проводника прямо пропорционально длине проводника, обратно пропорционально площади поперечного сечения и зависит от вещества:

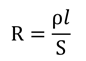
Из формулы мы можем выразить удельное сопротивление и определить его единицы измерения:

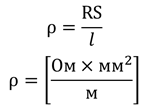
Упражнения.

Задача 1. Железный провод длиной 250 м имеет площадь поперечного сечения 2 мм². Найдите сопротивление данного провода.

Задача 2. Какое напряжение должно быть на эбонитовом диске толщиной 1 мм, чтобы через него прошел ток в 1 мкА? Диаметр диска составляет 1 см.

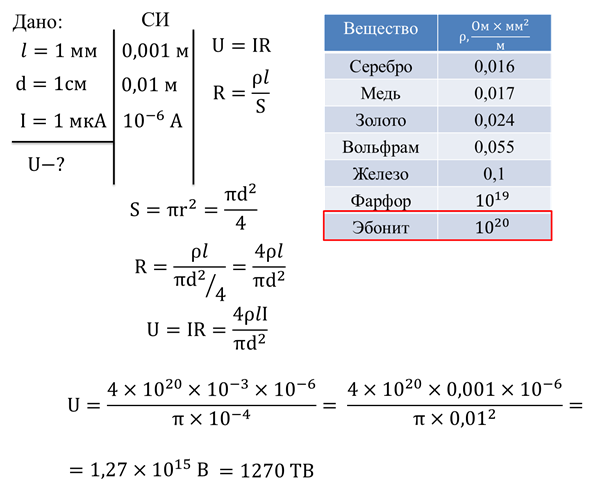
Мы видим, что даже для того, чтобы через эбонит прошел очень маленький ток, нужно просто огромное напряжение. Такое напряжение создать практически невозможно. Даже в современных ускорителях частиц достигалось напряжение не больше нескольких ТВ. Поэтому, можно сказать, что мы не можем провести ток через эбонит. Этого следовало ожидать, поскольку удельное сопротивление эбонита огромно, и он является непроводником.

Задача 3. На рисунке показан график зависимости силы тока на участке цепи от неизвестной величины. Можете ли вы определить, что это за величина?

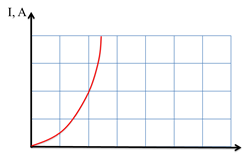
Итак, давайте вспомним, от чего вообще может зависеть сила тока. В первую очередь, сила тока — это количество заряда, прошедшего через поперечное сечение за единицу времени. Из формулы видно, что сила тока находится в линейной зависимости от количества заряда в единицу времени, а на рисунке мы видим график функции, который показывает нелинейную зависимость. Мы знаем, что график функции, описывающий любую линейную зависимость, будет являться прямой. Из формулы, описывающей закон Ома, мы видим, что сила тока прямо пропорциональна напряжению. Значит, неизвестная величина не является ни количеством заряда, ни напряжением. Сила тока обратно пропорциональна сопротивлению. Однако, мы уже знаем, что график функции зависимости силы тока от сопротивления представляет собой ветвь гиперболы, а на рисунке мы видим другой график.

Тогда следует заметить, что сила тока зависит от величин, которые, в свою очередь, зависят от других величин. Напряжение связано с работой по переносу заряда, но эта зависимость тоже линейная. Рассмотрим, от чего зависит сопротивление: от удельного сопротивления, от длины проводника и от площади поперечного сечения. Удельное сопротивление для каждого проводника — есть величина постоянная. Сопротивление находится в линейной зависимости от длины проводника, длина проводника — это независимая величина. Остается площадь поперечного сечения. Как раз-таки, она зависит не от радиуса, а от квадрата радиуса проводника, что приводит нас к нелинейной зависимости. Если мы преобразуем формулу, по которой вычисляется сила тока в проводнике, то увидим, что сила тока прямо пропорциональна квадрату радиуса проводника. Это единственная величина, которая могла привести к построению графика квадратичной функции. Действительно, если мы внимательно изучим график, то убедимся, что это парабола. Следует заметить, что это может быть график зависимости силы тока не от радиуса, а от диаметра. Однако, для того, чтобы это проверить, нам нужна дополнительная информация. Тем не менее, мы с уверенностью можем сказать, что это график зависимости силы тока либо от радиуса, либо от диаметра проводника (по форме эти два графика ничем не отличаются — существуют лишь числовые отличия).