Представим себе такую историю…
– Саша, ты меня звал? – спросил у друга Паша.
–
Да, звал, – ответил Саша. – Помоги мне, пожалуйста, разобраться. Я собрался
ехать на велосипеде в книжный магазин и спросил у старшего брата, как туда
проехать. Он мне объяснил, что сначала надо проехать  км
по дороге в сторону школы, а затем свернуть на дорогу, перпендикулярную той, по
которой я ехал. Это как?
км
по дороге в сторону школы, а затем свернуть на дорогу, перпендикулярную той, по
которой я ехал. Это как?
– Давай представим, что дороги – это у нас прямые. И твой брат сказал, что они перпендикулярны, – начал рассуждать Паша.

– А что это за перпендикулярные прямые? – перебил его Саша.
– Даже не знаю, – задумчиво ответил Паша и предложил, – а давай спросим у Мудряша.
– Ребята, прежде чем мы с вами поговорим, давайте немного разомнёмся и выполним устные задания, – предложил Мудряш.
– Теперь сверимся! – сказал Мудряш. – Посмотрите, что у вас должно было получиться!

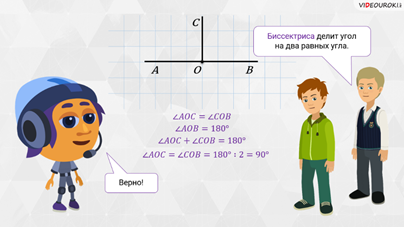
– А сейчас вернёмся к вашему вопросу и выясним, какие же прямые называют перпендикулярными, – начал Мудряш. – Ребята, давайте вспомним, какой угол называют развёрнутым.
–
Развёрнутым углом называют угол, равный 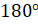 ,
– напомнили мальчишки.
,
– напомнили мальчишки.
–
Построим развёрнутый 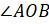 ,
– продолжил Мудряш. – Обратите внимание, что его стороны
,
– продолжил Мудряш. – Обратите внимание, что его стороны  и
и
 образуют
прямую. Теперь проведём биссектрису
образуют
прямую. Теперь проведём биссектрису 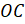 .
.

– Биссектриса делит угол на два равных угла, – вспомнил Паша.
– Верно! – отметил Мудряш.
–
А значит, 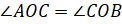 ,
– сказал Саша.
,
– сказал Саша.
–
Развёрнутый  ,
тогда можем записать, что
,
тогда можем записать, что 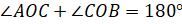 ,
– продолжил объяснять Мудряш. – А так как углы
,
– продолжил объяснять Мудряш. – А так как углы 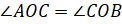 ,
то запишем:
,
то запишем: 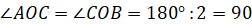 .
.
Если
мы с вами достроим луч 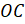 до
прямой
до
прямой 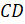 ,
то получим развёрнутый
,
то получим развёрнутый 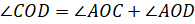 .
И эта сумма равна
.
И эта сумма равна  .
Выше мы выяснили, что
.
Выше мы выяснили, что 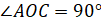 .
Выразим из предпоследнего равенства
.
Выразим из предпоследнего равенства 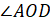 :
:
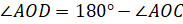 .
Подставим значение
.
Подставим значение  :
:
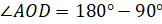 .
Выполним вычитание и получим, что
.
Выполним вычитание и получим, что 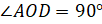 .
.
Таким
же образом мы можем показать, что и  .
.
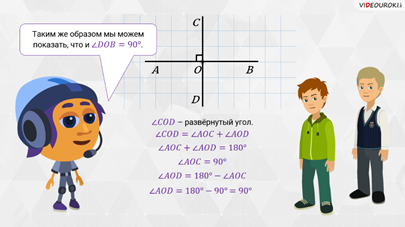
Итак,
при пересечении прямых  и
и
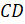 образовалось
четыре прямых угла.
образовалось
четыре прямых угла.
– И эти прямые называются перпендикулярными, – догадались Саша и Паша.
– Молодцы! – похвалил ребят Мудряш. – Запомните! Две прямые, образующие при пересечении четыре прямых угла, называют перпендикулярными прямыми.

Обозначают
перпендикулярные прямые вот так:  .
.
Прямые
можно обозначать и одной маленькой латинской буквой. Например, 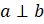 .
.
– А можно проверить, являются ли прямые перпендикулярными? – спросили у Мудряша мальчишки.
– Конечно. Проверить, перпендикулярны прямые или нет, можно, например, с помощью угольника, – начал объяснять Мудряш. – Для этого нам надо совместить точку пересечения прямых с вершиной прямого угла угольника и расположить его так, чтобы одна из прямых совпала со стороной прямого угла угольника.
– Тогда если вторая прямая совпадёт со второй стороной прямого угла угольника, то, значит, прямые пересекаются под прямым углом, – догадался Саша.
– Верно! – сказал Мудряш. – Следовательно, прямые перпендикулярны.

– А есть ещё какой-нибудь способ проверить, перпендикулярны ли прямые? – спросил Паша.
– Есть, – ответил Мудряш. – Это можно сделать с помощью транспортира. Для этого нам надо совместить точку пересечения прямых с центром транспортира и расположить транспортир так, чтобы одна из прямых прошла по линейке.
–
Тогда если вторая прямая проходит через штрих «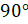 »,
то данные прямые пересекаются под прямым углом, – помог Мудряшу Саша.
»,
то данные прямые пересекаются под прямым углом, – помог Мудряшу Саша.
– А значит, эти прямые перпендикулярны, – добавил Паша.

– Молодцы! – похвалил ребят Мудряш. – Отметим, что совсем не обязательно измерять все четыре угла. Если один угол прямой, то и остальные три тоже будут прямыми.
– Давайте попробуем построить перпендикулярные прямые, – предложили мальчишки Мудряшу.
–
Построить перпендикулярные прямые также можно с помощью угольника или
транспортира, – начал Мудряш. – Чтобы построить перпендикулярные прямые с
помощью угольника, мы сначала проведём произвольную прямую 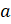 .
Возьмём угольник и совместим сторону его прямого угла с этой прямой. Затем
вдоль второй стороны прямого угла угольника проведём прямую
.
Возьмём угольник и совместим сторону его прямого угла с этой прямой. Затем
вдоль второй стороны прямого угла угольника проведём прямую 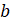 Таким
образом, мы получим перпендикулярные прямые
Таким
образом, мы получим перпендикулярные прямые 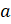 и
и
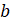 .
.
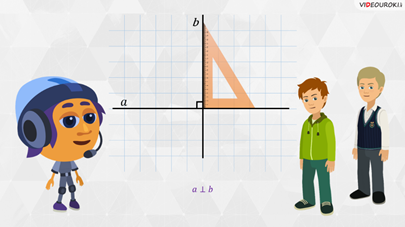
– Построить перпендикулярные прямые с помощью транспортира, наверное, будет сложнее, – задумались мальчишки.
–
Совсем нет, – успокоил ребят Мудряш. – Давайте снова проведём произвольную
прямую
 .
Приложим к этой прямой транспортир так, чтобы она прошла по линейке. Затем
найдём на шкале штрих, который соответствует
.
Приложим к этой прямой транспортир так, чтобы она прошла по линейке. Затем
найдём на шкале штрих, который соответствует 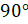 .
.
–
И проведём через него прямую, которая и будет перпендикулярна прямой  ,
– догадался Паша.
,
– догадался Паша.
–
И назовём эту прямую 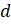 ,
– добавил Саша.
,
– добавил Саша.

– Всё верно! – отметил Мудряш и продолжил, – отметим, что с помощью угольника мы можем провести прямую, которая перпендикулярна данной, через некоторую точку. Причём эта точка может лежать на данной прямой, а может и не лежать.
Давайте
построим произвольную прямую 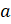 и
отметим на ней произвольную точку
и
отметим на ней произвольную точку  .
.
Возьмём
угольник и совместим сторону прямого угла угольника с нашей прямой 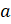 ,
а вершину прямого угла угольника совместим с точкой
,
а вершину прямого угла угольника совместим с точкой  .
.
Затем
проведём прямую 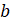 вдоль
второй стороны прямого угла угольника.
вдоль
второй стороны прямого угла угольника.
Вот
так мы с вами провели прямую 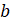 ,
перпендикулярную прямой
,
перпендикулярную прямой 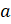 ,
через точку
,
через точку  ,
лежащую на прямой
,
лежащую на прямой 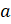 .
.

Ребята,
а сейчас давайте построим произвольную прямую  и
отметим произвольную точку
и
отметим произвольную точку 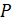 ,
которая не лежит на этой прямой.
,
которая не лежит на этой прямой.
–
И проведём через эту точку прямую, перпендикулярную прямой  ?
– заинтересованно спросили у Мудряша мальчики.
?
– заинтересованно спросили у Мудряша мальчики.
–
Да, – ответил Мудряш. – Для этого мы приложим угольник так, чтобы одна сторона
его прямого угла совпала с нашей прямой  ,
а вторая проходила через точку
,
а вторая проходила через точку 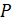 .
.
–
Затем проведём прямую вдоль второй стороны прямого угла угольника, – продолжил
построение Паша. – Можем назвать её, например, 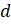 .
.
–
Получается, что мы провели прямую 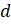 ,
перпендикулярную прямой
,
перпендикулярную прямой  ,
через точку
,
через точку 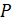 ,
которая не лежит на прямой
,
которая не лежит на прямой  ,
– сделали вывод Саша и Паша.
,
– сделали вывод Саша и Паша.

– Молодцы, ребята! – похвалил Пашу и Сашу Мудряш. – А теперь посмотрите на следующие рисунки. На них изображены перпендикулярные прямые, на которых лежат пары отрезков. Такие отрезки называют перпендикулярными.
Так,
на первом рисунке на перпендикулярных прямых 𝑎
и 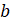 лежат
перпендикулярные отрезки
лежат
перпендикулярные отрезки  и
и
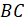 .
На втором рисунке на перпендикулярных прямых
.
На втором рисунке на перпендикулярных прямых  и
и
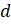 также
лежат перпендикулярные отрезки
также
лежат перпендикулярные отрезки 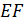 и
и
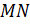 .
.

Перпендикулярными также могут быть два луча, луч и отрезок, отрезок и прямая, луч и прямая. Посмотрите на следующие рисунки.
–
На первом рисунке на перпендикулярных прямых 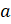 и
и
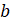 изображены
лучи
изображены
лучи  и
и
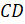 .
Они перпендикулярны, – сказали Саша и Паша.
.
Они перпендикулярны, – сказали Саша и Паша.
– Верно! – отметил Мудряш.

–
На втором рисунке на перпендикулярных прямых 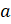 и
𝑏 изображены луч
и
𝑏 изображены луч  и
отрезок
и
отрезок 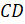 .
Они тоже перпендикулярны, – продолжили ребята, и у них возник вопрос, – а что
на третьем рисунке?
.
Они тоже перпендикулярны, – продолжили ребята, и у них возник вопрос, – а что
на третьем рисунке?
–
На следующем рисунке у нас изображены перпендикулярные прямые 𝑎
и 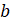 .
На прямой
.
На прямой 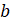 лежит
отрезок
лежит
отрезок  ,
– начал объяснять Мудряш.
,
– начал объяснять Мудряш.
–
А значит, отрезок  перпендикулярен
прямой
перпендикулярен
прямой 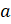 ,
– догадался Паша и продолжил, – тогда на последнем рисунке, так как прямые
,
– догадался Паша и продолжил, – тогда на последнем рисунке, так как прямые 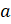 и
и
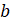 перпендикулярны,
луч
перпендикулярны,
луч  перпендикулярен
прямой
перпендикулярен
прямой 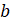 .
.
– Правильно, – сказал Мудряш и задал вопрос, – Саша, Паша, а какие геометрические фигуры, элементы которых перпендикулярны, вы знаете?
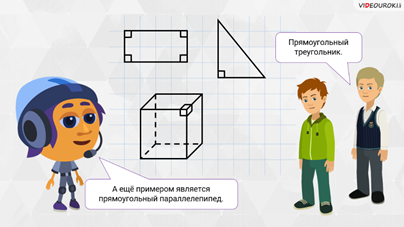
– Прямоугольник, – сразу же ответил Саша.
– Да, любые его две соседние стороны перпендикулярны, – добавил Мудряш.
– Прямоугольный треугольник, – привёл пример Паша, – так как один из его углов равен девяноста градусам.
– А ещё примером является прямоугольный параллелепипед, ведь он состоит из шести прямоугольников, а мы выше сказали, что у прямоугольника любые две соседние стороны перпендикулярны.
– Ребята, а сейчас давайте выполним задание, чтобы закрепить навыки построения перпендикулярных прямых, – сказал Мудряш.
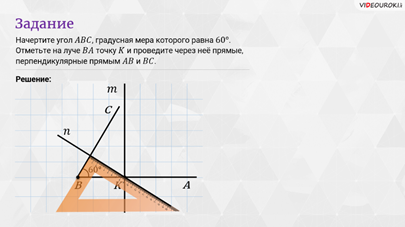
Задание:
Начертите
угол  ,
градусная мера которого равна
,
градусная мера которого равна  .
Отметьте на луче
.
Отметьте на луче  точку
точку
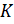 и
проведите через неё прямые, перпендикулярные прямым
и
проведите через неё прямые, перпендикулярные прямым  и
и
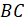 .
.
Решение: в
первую очередь мы с вами построим угол, равный  .
Для этого отметим произвольную точку
.
Для этого отметим произвольную точку  .
Затем начертим луч
.
Затем начертим луч  с
началом в этой точке
с
началом в этой точке  .
Теперь приложим к этому лучу транспортир так, чтобы его центр совпал с точкой
.
Теперь приложим к этому лучу транспортир так, чтобы его центр совпал с точкой  ,
а сам луч прошёл через начало отсчёта на шкале. Найдём на шкале транспортира
штрих, который соответствует
,
а сам луч прошёл через начало отсчёта на шкале. Найдём на шкале транспортира
штрих, который соответствует  ,
и проведём через него луч
,
и проведём через него луч 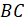 .
Таким образом, мы построили угол
.
Таким образом, мы построили угол  ,
который равен
,
который равен  .
.
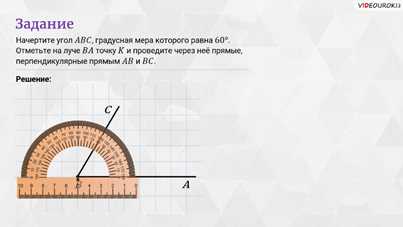
Отметим
на луче  точку
точку
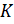 .
Проведём через неё сначала прямую, перпендикулярную прямой
.
Проведём через неё сначала прямую, перпендикулярную прямой  .
Для этого воспользуемся угольником. Совместим сторону его прямого угла с прямой
.
Для этого воспользуемся угольником. Совместим сторону его прямого угла с прямой
 ,
а вершину прямого угла – с точкой
,
а вершину прямого угла – с точкой 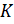 .
И проведём прямую
.
И проведём прямую  вдоль
второй стороны прямого угла нашего угольника.
вдоль
второй стороны прямого угла нашего угольника.

Теперь
проведём через точку 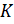 прямую,
перпендикулярную прямой
прямую,
перпендикулярную прямой 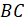 .
.
Приложим
угольник так, чтобы одна сторона его прямого угла совпала с нашей прямой 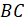 ,
а вторая проходила через точку
,
а вторая проходила через точку 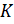 .
Теперь проведём прямую вдоль второй стороны прямого угла угольника и назовём её
.
Теперь проведём прямую вдоль второй стороны прямого угла угольника и назовём её
 .
.
Итак,
мы провели прямые  и
и
 ,
которые перпендикулярны соответственно прямым
,
которые перпендикулярны соответственно прямым  и
и
 .
.

 Получите свидетельство
Получите свидетельство Вход
Вход



 1
1 3901
3901





Спасибо!
Детям ваши уроки очень нравятся!