Фотон. Уравнение Эйнштейна для фотоэффекта

Изучая опыты Александра Григорьевича Столетова, мы с вами смогли сформулировать три основных закона внешнего фотоэффекта. Однако все попытки экспериментально объяснить наблюдаемые зависимости на основе законов электродинамики Максвелла, согласно которым свет — это электромагнитная волна, непрерывно распределённая в пространстве, оказались безрезультатными. Было абсолютно не ясно, почему энергия фотоэлектронов определяется только частотой света и почему лишь при достаточно малой длине волны свет вырывает электроны.

Для того, чтобы убрать возникшие противоречия, немецкий учёный Макс Планк выдвинул гипотезу, согласно которой атомы испускают электромагнитную энергию не непрерывно, а отдельными порциями — квантами. При этом энергия каждой порции прямо пропорциональна частоте излучения:

Е = hν.

Фундаментальная постоянная, входящая в это уравнение, была названа постоянной Планка, хотя сам Планк называл её «таинственным послом из реального мира»:

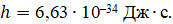
Из гипотезы Планка следовало, что отдельный осциллятор может обладать не любой энергией, а лишь энергией, кратной hν. Таким образом, впервые появилась идея о квантовании энергии.

Развивая идеи Макса Планка, Альберт Эйнштейн в 1905 году для объяснения экспериментальных законов внешнего фотоэффекта выдвинул гипотезу о дискретности самого электромагнитного излучения: свет излучается, поглощается и распространяется в виде отдельных порций (квантов).

По гипотезе Эйнштейна, монохроматическое электромагнитное излучение частотой v обладает не только волновыми свойствами, но и свойствами, характерными для потока частиц. Каждая такая частица движется со скоростью света и несёт квант энергии. В 1928 году американский физик Артур Комптон предложил называть эти частицы фотонами, что в переводе с древнегреческого означало «свет».

Энергию фотона можно выразить и через длину волны, используя соответствующее соотношение:

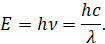
Так же энергию фотона часто выражают и через циклическую частоту. При этом в формуле для энергии фотона в качестве коэффициента пропорциональности вместо постоянной Планка используют величину

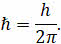
Читается она как «Аш с чертой», и называется постоянной Дира́ка:

На одном из прошлых уроков мы с вами показали, что частица, движущаяся со скоростью, близкой к скорости света, обладает релятивистским импульсом, который связан с энергией частицы выражением, представленным на экране:

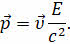
Если учесть, что фотон распространяется со скоростью света, то его импульс можно определить по одному из следующих уравнений:

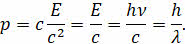
Отсюда получаем, что энергию фотона можно определить, как произведение его импульса и скорости света:

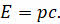
Теперь вспомним, как связаны между собой энергия и импульс релятивистской частицы:

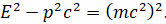
При подстановке в эту формулу энергии фотона находим, что масса фотона (а точнее, масса покоя фотона) равна нулю.

Оказывается, что фотон — это удивительная частица, которая обладает энергией, импульсом, но вследствие того, что скорость его движения всегда равна скорости распространения света, его масса покоя равна нулю. Напомним, что такие частицы называют безмассовыми.

Следовательно, фотон существует лишь пока он движется. Но несмотря на это, фотон является самой распространённой по численности частицей во Вселенной. На один нуклон (то есть на одно атомное ядро) приходится не менее 20 миллиардов фотонов.

Обобщив выше сказанное мы можем выделить следующие свойства фотона:

·                    существует только в движении;

·                    является безмассовой частицей;

·                    электрически нейтрален;

·                    модуль его скорости движения равен модулю скорости распространения света в вакууме во всех ИСО;

·                    его энергия пропорциональна частоте соответствующего электромагнитного излучения;

·                    модуль импульса фотона равен отношению его энергии к модулю скорости.

Таким образом, при освещении электрода электромагнитным излучением происходит взаимодействие фотонов с электронами вещества. Если энергия фотона достаточно велика, то какой-либо из электронов после поглощения фотона может получить энергию, достаточную для того, чтобы покинуть облучаемое тело. Электроны, покинувшие образец, имеют некоторую скорость, поэтому даже при отсутствии напряжения между электродами сила фототока не равна нулю.

Для того чтобы покинуть вещество, электрон должен совершить работу против сил связи электрона с атомами вещества. Она называется работой выхода. Для металлов эта работа связана с преодолением сил взаимодействия электронов с положительно заряженными ионами кристаллической решётки, которые удерживают электрон в веществе. Работа выхода для металлов обычно составляет несколько электронвольт.

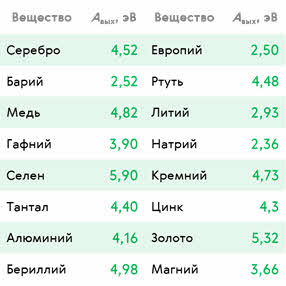
Электронвольт — это энергия, которую приобретёт частица с зарядом, равным элементарному, при перемещении между двумя точками с ускоряющей разностью потенциалов 1 В:

1 эВ =1,6 ∙ 10^–19 Дж.

Оставшаяся часть энергии поглощённого кванта составляет кинетическую энергию освободившегося электрона. Наибольшей кинетической энергией будут обладать те электроны, которые поглотят кванты света вблизи поверхности металла и вылетят из него, не успев потерять энергию при столкновениях с другими частицами в металле.

На основе закона сохранения энергии можно записать следующее уравнение для фотоэлектрона:

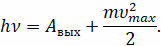
Это соотношение называют уравнением Эйнштейна для внешнего фотоэффекта.

Теперь, познакомившись с фотоном и уравнением Эйнштейна, можно приступить к объяснению экспериментальных законов фотоэффекта.

Итак, первый закон фотоэффекта утверждает, что сила фототока насыщения пропорциональна общему числу фотоэлектронов, покидающих поверхность металла за единицу времени. Число же таких фотоэлектронов пропорционально числу фотонов, падающих на поверхность за это же время. Обратите внимание, что именно пропорционально, а не равно, так как часть квантов света поглощается кристаллической решёткой, и их энергия переходит во внутреннюю энергию металла (он нагревается). Поэтому логично, что при увеличении интенсивности падающего света бо́льшее количество фотонов будут взаимодействовать с веществом. А это приводит к росту числа фотоэлектронов, покидающих поверхность металла.

Второй закон фотоэффекта говорит нам о том, что максимальная кинетическая энергия фотоэлектронов прямо пропорциональна частоте падающего на катод излучения и не зависит от интенсивности этого излучения.

И действительно, фотоэлектрон вырывается из катода за счёт действия одного кванта падающего излучения (одного фотона). Поэтому кинетическая энергия фотоэлектрона зависит не от полной энергии волны, а от энергии одного кванта, которая, как мы помним, линейно зависит от частоты излучения. При увеличении частоты падающего света максимальная кинетическая энергия фотоэлектронов возрастает линейно, как следует из уравнения Эйнштейна для фотоэффекта:

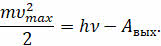
И, наконец, третий закон фотоэффекта: для каждого вещества существует минимальная частота света, называемая красной границей фотоэффекта, ниже которой фотоэффект невозможен.

Действительно, если частота падающего излучения меньше граничной частоты, при которой энергия кванта света равна работе выхода (hv_min = A_вых), то испускания электронов не происходит.

Из этого соотношения легко найти красную границу фотоэффекта:  

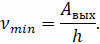
Так как h — это постоянная величина, то из формулы следует, что красная граница фотоэффекта зависит только от работы выхода электронов (иными словами, определяется только строением металла и состоянием его поверхности).

Используя соотношение между длиной волны и её частотой, можно получить формулу для определения длины волны излучения, соответствующей красной границе фотоэффекта:

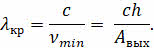
Для закрепления нового материала решим с вами такую задачу. Определите задерживающее напряжение между электродами фотоэлемента при освещении его светом с длиной волны 200 нм, если работа выхода электронов из металла равна 4 эВ.

В заключение отметим, что явление фотоэффекта нашло широкое применение не только в технике, но и в нашей с вами повседневной жизни. Приборы, принцип действия которых основан на явлении фотоэффекта, называют фотоэлементами.

Фотоэлементами оборудуются многие автоматические станки на производстве, для прерывания их работы в чрезвычайных ситуациях (например, при попадании руки человека в рабочую зонe пресса). Фотоэлементы применяются для выдвигания преграды в турникете метро, автоматического включение освещения на улицах, включения воды в кране и сушилки для рук. Их используют и в военном деле в самонаводящихся снарядах, для сигнализации и локации невидимыми лучами. С помощью фотоэлементов осуществляется воспроизведение звука, записанного на киноплёнке. Фотоэлементы нашли применение и в сортировке массовых изделий по размерам и окраске. Их широко применяют при производстве солнечных батарей, устанавливаемых на космических спутниках.

Как видим, явление фотоэффекта, открытое более 120 лет назад Генрихом Герцем, широко вошло в нашу повседневную жизнь и подарило множество замечательных приборов и открытий.