Преобразования графиков функций

Вопросы занятия:

·  повторить основные преобразования графиков функций.

Материал урока

Сегодня на уроке мы рассмотрим, как, если мы знаем график функции f(x) построить графики функции:

И начнём мы рассматривать случай, когда, зная график функции y = f(x) нам надо построить график функции y = f(x + a).

Для этого необходимо осуществить параллельный перенос графика функции игрек равно f(x) вдоль оси абсцисс на a единичных отрезков вправо, если a < 0 и влево, если a > 0.

Например.

Пример.

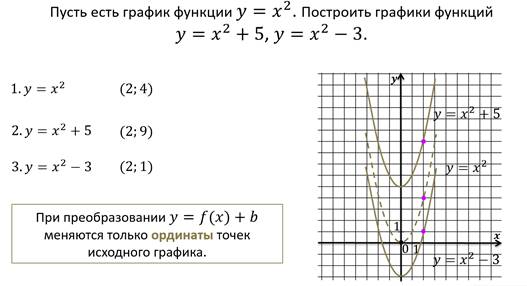
Теперь давайте построим график функции y = f(x) + b, если мы знаем график функции y = f(x).

Для этого необходимо осуществить параллельный перенос графика функции y = f(x) вдоль оси ординат на b единичных отрезков вверх, если b > 0 и вниз, если b < 0.

Например,

Пример.

Иногда приходится решать задания, в которых преобразование графиков представляет собой комбинацию элементарных преобразований.

Пример.

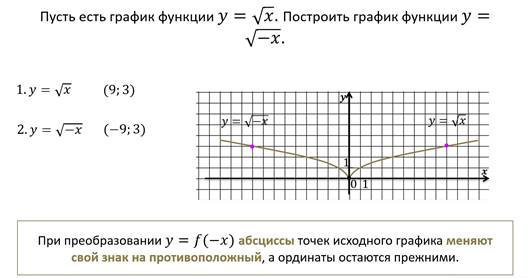
Теперь давайте посмотрим, как, зная график функции y = f(x), построить график функции y = f(-x).

Для этого необходимо график функции y = f(x) симметрично отобразить относительно оси ординат.

Пример.

Теперь рассмотрим построение преобразования y = -f(x). Для того, чтобы построить график функции y = -f(x), необходимо график функции y = f(x) симметрично отобразить относительно оси абсцисс.

Пример.

Теперь давайте рассмотрим, как, зная график функции y = f(x), можно построить график функции y = f(kx). Для этого необходимо выполнить следующие преобразования графика функции y = f(x): при k > 1 – сжатие графика к оси ординат в k раз, если 0 < k < 1, то надо выполнить растяжение графика от оси ординат в k раз.

Рассмотрим пример.

Пример.

Теперь давайте рассмотрим преобразование y = mf(x). Для построения такого преобразования, необходимо выполнить следующие преобразования графика функции y = f(x): при m > 1 – надо выполнить растяжение графика от оси абсцисс в m раз, при 0 < m <1, надо произвести сжатие графика к оси абсцисс в m раз.

Рассмотрим пример.

Пример.

Теперь давайте рассмотрим преобразование y = f(│x│).

Для этого преобразования необходимо ту часть графика, которая соответствует x > 0, оставить без изменения, а часть графика, которая соответствует x < 0, симметрично отобразить относительно оси ординат.

Теперь давайте рассмотрим преобразование y = │f(x)│.

Для этого преобразования необходимо ту часть графика, которая соответствует y > 0, оставить без изменения, а часть графика, которая соответствует y < 0, симметрично отобразить относительно оси абсцисс.

Например,

Теперь давайте рассмотрим несколько примеров.

Пример.

Обратите внимание, что в данном примере только один вариант решения. Потому что, если:

Итоги урока

Сегодня на уроке, мы рассмотрели элементарные преобразования графиков функций.