Раскрытие скобок

Часто при решении примеров удобно раскрыть скобки в выражении, нежели подсчитывать их значения. Сегодня на уроке мы рассмотрим, как правильно раскрывать скобки.

Итак, рассмотрим случаи, когда перед скобками стоит знак «+». Для этого воспользуемся хорошо известным для вас сочетательным свойством сложения:

Если к числу нужно прибавить сумму двух чисел, то можно сначала к этому числу прибавить первое слагаемое, а затем второе.

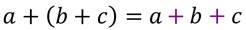
Обратите внимание, на экране записано два выражения соединённых знаком равенства. Вот только левая часть равенства содержит скобки, а правая – без скобок. Говорят, что при переходе от левой части равенства к правой произошло раскрытие скобок.

Рассмотрим ещё одно выражение:

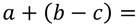
Как вы думаете, можно ли его преобразовать в выражение без скобок?

Можно. Вы знаете, что вычитание можно заменить сложением. Так и поступим, заменим в этом выражении вычитание сложением.

И давайте попробуем преобразовать ещё два выражения со скобками: 

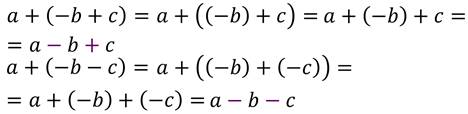
Опустим все промежуточные рассуждения и приравняем начальные и конечные части равенств.

Обратите внимание, перед каждой из скобок стоит знак «+».

Сделаем вывод:

Если перед скобками стоит знак «+», то можно опустить скобки и этот знак «+», сохранив знаки слагаемых, стоящих в скобках.

Если первое слагаемое в скобках записано без знака, то его надо записать со знаком «+».

Задание

Раскройте скобки и найдите значения выражений.

Мы разобрали случаи, когда перед скобками стоит знак «+». А как же поступить, если перед скобками стоит знак «».

Давайте рассмотрим выражение: – (2 + 3).

Найти значение этого выражения можно, сложив 2 и 3, а затем взять полученное число с противоположным знаком.

Тот же самый результат можно получить и другим способом. Для этого мы сложим числа противоположные исходным.

Сформулируем правило:

Если перед скобками стоит знак «–», то скобки и этот знак «минус» можно убрать, а знаки перед числами внутри скобок изменить на противоположные.

Например, раскроем скобки в выражениях.

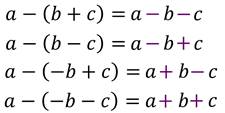
Задание

Раскройте скобки и найдите значения выражений.

Для раскрытия скобок в выражениях, содержащих умножение числа на сумму, используется распределительное свойство умножения:

По правилам умножения рациональных чисел, если a > 0, то знаки слагаемых b и c не изменятся, а если a <0, то изменятся на противоположные.

Например

Итоги

Если перед скобками стоит знак «+», то можно опустить скобки и этот знак «+», сохранив знаки слагаемых, стоящих в скобках.

Если первое слагаемое в скобках записано без знака, то его надо записать со знаком «+».

Если перед скобками стоит знак «–», то скобки и этот знак «минус» можно убрать, а знаки перед числами внутри скобок изменить на противоположные.