На этом уроке мы познакомимся с понятиями «отрезок», «прямая», «луч» и «плоскость». Рассмотрим расположение точек, отрезков, прямых и лучей в плоскости.
На прошлом уроке мы разобрались, как строить отрезок. Мы уже знаем, что отрезок – это прямая линия, ограниченная двумя точками.
Определение
Давайте начертим отрезок MN. Если продлить этот отрезок неограниченно за точку N, то мы получим новую фигуру, которая называется луч. У нас получился луч MN.

Точку М называют началом луча.
Если бы мы продлевали отрезок MN неограниченно за точку М, то у нас бы получился луч NМ, у которого точка N – начало луча.

Заметьте: обозначается луч большими заглавными буквами латинского алфавита, первой буквой записывают его начало, а затем букву, обозначающую какую-либо другую точку луча.
Обратите внимание, что луч имеет начало, но не имеет конца, т. е. он бесконечен в одну сторону.
Для того чтобы представить луч в окружающей среде, достаточно сфотографировать след от самолёта в безоблачном небе, где сам самолёт – это начальная точка, а след, оставленный на небе, – это прямая линия, которая бесконечна.

Либо солнечный луч, где начальная точка – это солнце, а конечной точки нет.

Определение
Если отрезок MN неограниченно продлевать в обе стороны – как за точку М, так и за точку N, то у нас получится фигура, которая называется прямой.

На рисунке у нас получилась прямая MN, также её можно назвать и прямая NМ. Как кому больше нравится!
Заметьте, что прямая не имеет ни начала, ни конца.
Любая точка прямой разделяет её на 2 луча.

В нашем случае точка О разделяет прямую MN на луч ОМ и луч ОN. Лучи, на которые точка разбивает прямую, называют дополнительными друг другу.
Представление о прямой можно получить, если сложить лист бумаги (линия, которая получилась при сгибе, и будет прямой) или туго натянуть верёвку.


В математике прямая представляется идеально ровной и бесконечной в обе стороны.
Прямую можно обозначить двумя вариантами.
1-й вариант: двумя заглавными буквами латинского алфавита, например MN. В таком случае говорят: «Прямая MN».
2-й вариант: прямую обозначают одной малой буквой, например m, и говорят: «Прямая m».
Давайте попробуем провести ещё одну прямую через эти же две точки.
У нас это не получится. Через любые две точки можно провести только одну прямую!
Точки, отрезки, лучи и прямые располагаются в плоскости. Примеры плоскостей в жизни мы встречаем каждый день. Представление о плоскости дают поверхности стола, оконного стекла или замёрзшего водоёма.



Только эти поверхности имеют границы, а плоскость в математике безгранична во всех направлениях. Мы рисуем фигуры на «кусках» плоскости, например в тетрадном листе или на школьной доске.
Теперь давайте рассмотрим расположение точек, отрезков, прямых и лучей в плоскости.
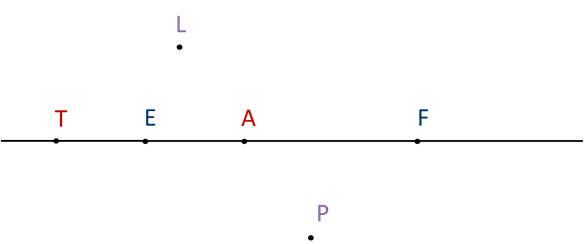
На рисунке изображены прямая EF и точки А, L, P и T. Точки А, E, F лежат на отрезке EF, а точки L, P, T не лежат на этом отрезке. Посмотрите, как это записывается.

Точки А, E, F лежат на луче EF, а точки А, E, F, Т лежат на луче FЕ. Посмотрите запись этих утверждений.

Точки А, E, F, Т лежат на прямой EF, а точки А, P, L – на прямой PL.
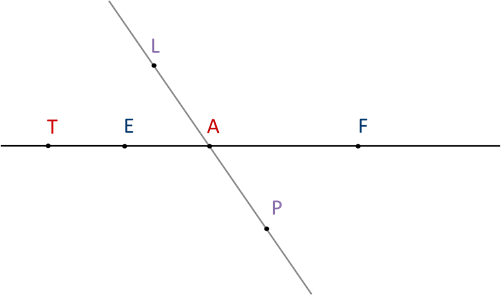
Обозначается это так:

Точка А лежит между точками Е и F. Точка L не лежит между точками Е и F, она находится вне отрезка EF. Точка Е лежит между точками А и Т, а точка А – между точками P и L.
На следующем рисунке изображены прямая a и прямая b.
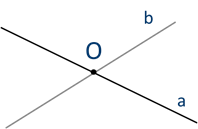
Если две прямые имеют одну общую точку, то говорят, что они пересекаются в этой точке. В нашем примере прямые а и b пересекаются в точке О. Точка О делит каждую прямую на две части. Точка О – точка пересечения прямых.
Посмотрите на взаимное расположение прямых m и n:

Они не имеют общих точек. Если прямые не имеют общих точек, то говорят, что они параллельны.
Запомните!
· Прямая бесконечна.
· Отрезок ограничен.
· Луч имеет начало, но не имеет конца.
· Плоскость бесконечна.
Итоги
Итак, на уроке мы с вами разобрались в отличиях понятий «отрезок», «прямая», «луч». Научились их строить. Узнали, что такое плоскость, а также рассмотрели расположение точек, отрезков, прямых и лучей в плоскости.

 Получите свидетельство
Получите свидетельство Вход
Вход



 0
0 6092
6092

