Данная тема посвящена решению задач на математический и пружинный маятники.
Задача 1. Как надо изменить жёсткость пружины маятника, чтобы увеличить частоту его колебаний в 2 раза?

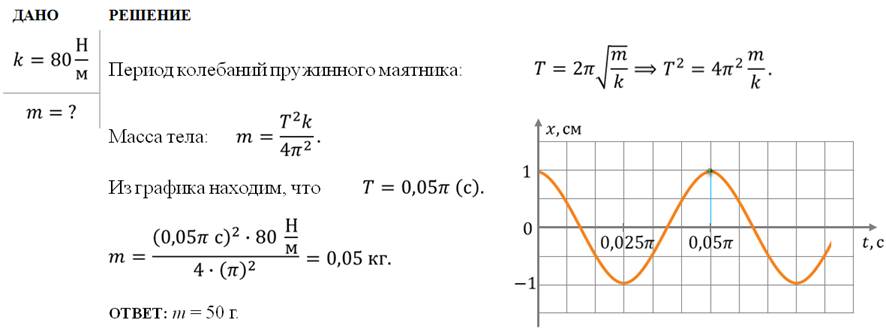
Задача 2. Небольшое тело, закрепленное на пружине жесткостью восемьдесят ньютон на метр, совершает гармонические колебания. График зависимости координаты этого тела от времени изображен на рисунке. Определите массу тела.
Задача 3. Самый высокогорный город мира — маленький перуанский шахтёрский городок Серро-де-Паско, расположенный в Центральных Андах на высоте 4380 метров над уровнем моря. На сколько будут отставать маятниковые часы за сутки, выверенные на уровне моря, если их поднять на эту высоту? Принять маятник в часах за математический, а Rз = 6370 км.



Задача 4. В ракете установлен математический маятник длиной l. Чему будет равен период колебаний такого маятника, если ракета начнёт подниматься с Земли вертикально вверх с ускорением а?
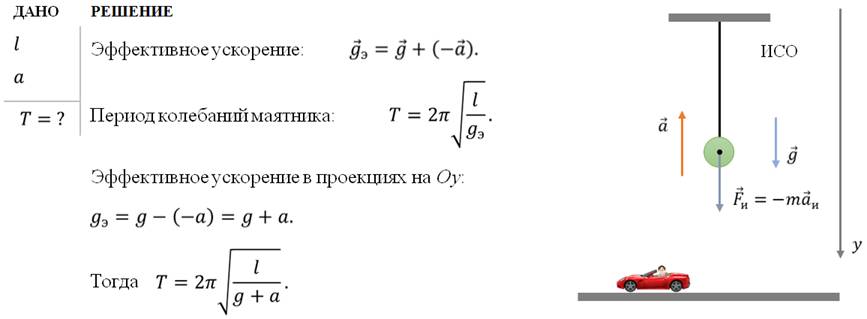
Задача 5. Шарик массой 1 кг совершает колебания в системе, показанной на рисунке. Жёсткости пружин равны 100 Н/м и 150 Н/м. Если в положении равновесия пружины не деформированы, то чему равен период колебаний тела? Силами сопротивления пренебречь.
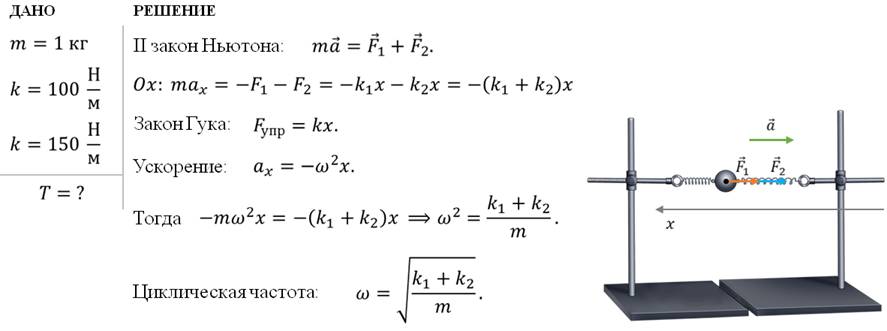
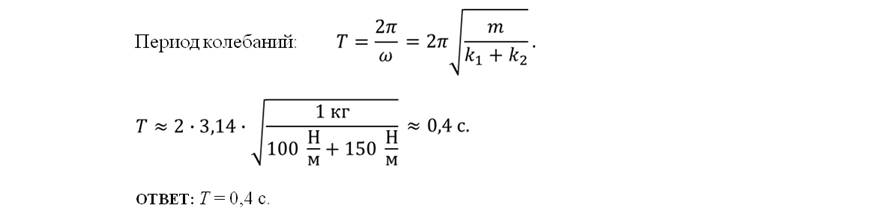
«Наше счастье зависит в большей степени от того,
как мы встречаем события нашей жизни,
чем от природы самих событий».
Александр фон Гумбольдт

 Получите свидетельство
Получите свидетельство Вход
Вход




 0
0 13930
13930

