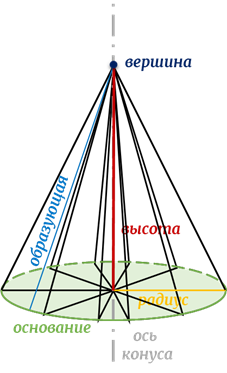
Напомним, что конус – это тело, полученное при вращении прямоугольного треугольника вокруг прямой, проходящей через один из его катетов.
Назовём элементы конуса.
Осью конуса называется прямая вращения.
Основание конуса
– круг радиуса 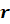 ,
который равен катету треугольника вращения.
,
который равен катету треугольника вращения.
Радиус
конуса 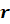 –
это радиус его основания.
–
это радиус его основания.
Вершина конуса – неподвижная вершина треугольника вращения.
Образующая
конуса 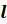 –
отрезок, соединяющий вершину конуса с любой точкой окружности основания. Все
образующие конуса равны между собой.
–
отрезок, соединяющий вершину конуса с любой точкой окружности основания. Все
образующие конуса равны между собой.
Высота конуса
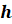 –
перпендикуляр, опущенный из вершины конуса на плоскость его основания. Высота
конуса совпадает с неподвижным катетом треугольника вращения.
–
перпендикуляр, опущенный из вершины конуса на плоскость его основания. Высота
конуса совпадает с неподвижным катетом треугольника вращения.
В
конусе радиус основания 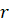 ,
высота
,
высота 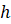 и
образующая
и
образующая 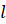 связаны
следующим соотношением:
связаны
следующим соотношением:
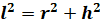 .
.
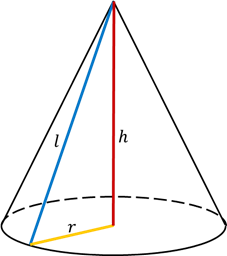
Сечение конуса плоскостью, проходящей через его вершину, представляет собой равнобедренный треугольник, у которого боковые стороны являются образующими конуса.
Осевым сечением конуса называется сечение конуса плоскостью, проходящей через его ось.
Осевое сечение конуса – равнобедренный треугольник, боковые стороны которого – образующие, а основание – диаметр основания конуса.
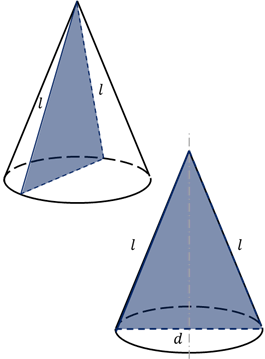
Боковую поверхность конуса, как и боковую поверхность цилиндра, можно развернуть на плоскость, разрезав её по одной из образующих. Развёрткой боковой поверхности конуса является круговой сектор.
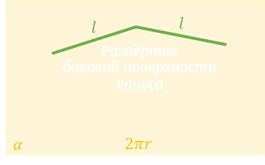
Обратите
внимание, радиус сектора равен образующей 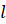 конуса,
а длина дуги сектора равна длине окружности основания конуса.
конуса,
а длина дуги сектора равна длине окружности основания конуса.
Площадь боковой поверхности конуса можно вычислить по следующим формулам:
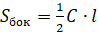 ,
,
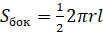 ,
,
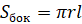 ,
,
где
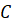 –
длина окружности основания,
–
длина окружности основания, 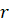 –
радиус основания,
–
радиус основания, 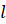 –
образующая.
–
образующая.
Площадь полной поверхности конуса равна сумме площади боковой поверхности конуса и площади его основания.
Тогда площадь полной поверхности конуса можно вычислить по формуле^
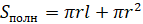 ,
,
где
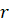 –
радиус основания конуса,
–
радиус основания конуса, 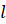 –
его образующая.
–
его образующая.
Объём конуса равен одной третьей произведения площади основания на высоту.
Тогда его можно вычислить по формуле:
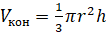 ,
,
где
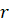 –
радиус основания конуса,
–
радиус основания конуса, 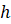 –
его высота.
–
его высота.
Плоскость, параллельная плоскости основания конуса, пересекает конус по кругу, а боковую поверхность – по окружности с центром на оси конуса. Эта плоскость разбивает конус на две части. Одна из частей (верхняя) представляет собой конус, а вторая (нижняя) называется усечённым конусом.
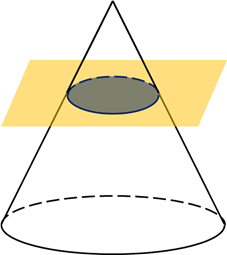
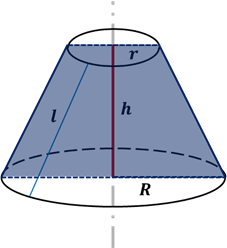
Усечённым
конусом называется часть конуса, ограниченная его основанием
и сечением, параллельным плоскости основания. Усечённый конус имеет ось,
высоту 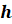 ,
радиусы оснований
,
радиусы оснований 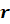 и
и
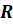 ,
образующую
,
образующую 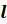 .
Осевое сечение усечённого конуса – равнобедренная трапеция.
.
Осевое сечение усечённого конуса – равнобедренная трапеция.
Площадь боковой поверхности усечённого конуса и объём усечённого конуса равен разности площадей боковых поверхностей и объёмов полного конуса и отсечённого.
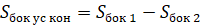 ,
,
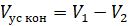
Площадь боковой поверхности усечённого конуса можно найти по следующим формулам:
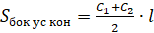 ,
,
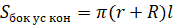
Объём усечённого конуса можно вычислить по следующим формулам:
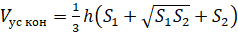 ,
,
где
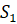 и
и
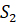 –
площади оснований,
–
площади оснований, 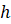 –
высота усечённого конуса;
–
высота усечённого конуса;
или
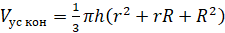 ,
,
где
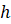 –
высота усечённого конуса,
–
высота усечённого конуса, 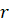 и
и
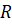 –
радиусы верхнего и нижнего оснований.
–
радиусы верхнего и нижнего оснований.
Основные моменты мы с вами повторили, а теперь давайте перейдём к практической части занятия.
Задача
первая. Радиус основания конуса равен 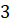 см,
высота конуса равна
см,
высота конуса равна 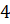 см.
Найдите площадь боковой поверхности и объём конуса.
см.
Найдите площадь боковой поверхности и объём конуса.
Решение.

Задача
вторая. В конус вписана правильная треугольная пирамида с
площадью основания 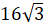 см2
и углом наклона бокового ребра к основанию, равным
см2
и углом наклона бокового ребра к основанию, равным 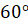 .
Найдите объём и площадь полной поверхности конуса.
.
Найдите объём и площадь полной поверхности конуса.
Решение.
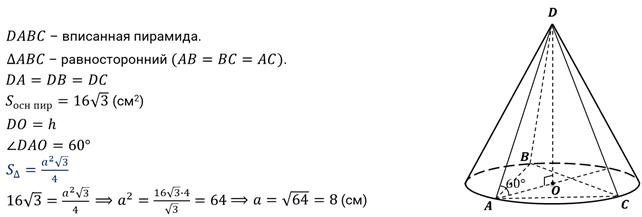
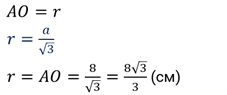
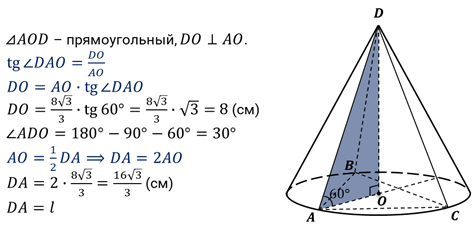
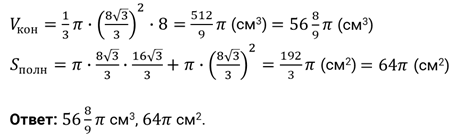
Задача
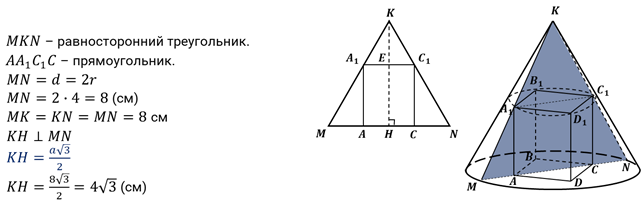
третья. В равносторонний конус с радиусом основания, равным 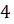 см,
вписан прямоугольный параллелепипед в основании которого лежит квадрат, с
высотой
см,
вписан прямоугольный параллелепипед в основании которого лежит квадрат, с
высотой 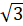 см
так, что одно его основание принадлежит основанию конуса, а вершины другого
основания принадлежат боковой поверхности конуса. Найдите объём
параллелепипеда. В ответе запишите значение
см
так, что одно его основание принадлежит основанию конуса, а вершины другого
основания принадлежат боковой поверхности конуса. Найдите объём
параллелепипеда. В ответе запишите значение 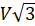 .
.
Решение.
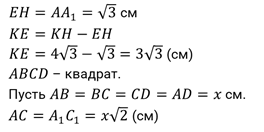
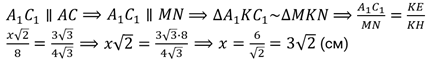

Задача
четвёртая. Длины радиусов оснований и образующей усечённого
конуса равны соответственно 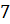 см,
см,
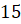 см
и
см
и 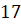 см.
Вычислите его высоту.
см.
Вычислите его высоту.
Решение.

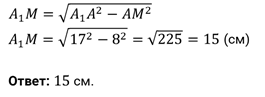

 Получите свидетельство
Получите свидетельство Вход
Вход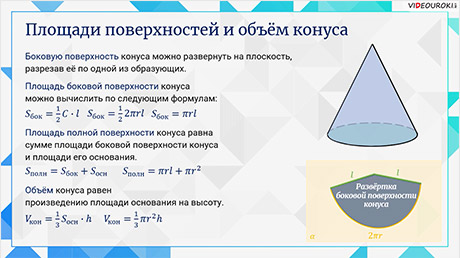




 20546
20546

