Цилиндр. Площади поверхностей. Объём

Напомним, что цилиндр – это тело, полученное при вращении прямоугольника вокруг прямой, проходящей через одну из его сторон.

Назовём элементы цилиндра.

Основания цилиндра – два равных круга радиуса .

Отрезок, соединяющий окружности оснований и перпендикулярный основаниям, называется образующей цилиндра и обозначается . Все образующие цилиндра параллельны и равны.

Осью цилиндра называется прямая, проходящая через центры оснований. Она параллельна образующим.

Высота цилиндра  – перпендикуляр, опущенный из любой точки одного основания на другое, или другими словами, это расстояние между плоскостями оснований цилиндра. Образующая цилиндра равна его высоте.

Радиусом цилиндра называется радиус его основания.

Цилиндр называется равносторонним, если его высота равна диаметру основания.

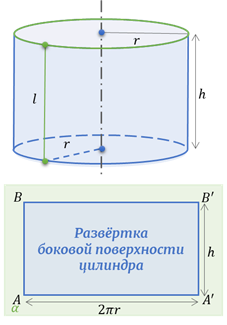
Осевым сечением цилиндра называется сечение цилиндра плоскостью, проходящей через его ось. Осевое сечение цилиндра – прямоугольник, две стороны которого есть образующие цилиндра, а две другие – диаметры его оснований.

Сечение, параллельное оси цилиндра, является прямоугольником.

Сечение, перпендикулярное оси цилиндра, является кругом, равным основаниям цилиндра.

Боковая поверхность цилиндра может быть развёрнута в прямоугольник со сторонами, одна из которых равна длине окружности основания, другая – высоте цилиндра.

Площадь боковой поверхности цилиндра можно вычислить по следующим формулам:

, , ,

где  – длина окружности основания,  – высота цилиндра,  – радиус основания,  – образующая.

Площадь полной поверхности цилиндра равна сумме площади боковой поверхности цилиндра и двух площадей его оснований.

Тогда площадь полной поверхности цилиндра можно вычислить по формуле:

,

где  – радиус оснований цилиндра,  – его высота.

Объём цилиндра равен произведению площади основания на высоту.

Тогда его можно вычислить по формуле:

,

где  – радиус оснований цилиндра,  – его высота.

Основные моменты мы с вами повторили, а теперь давайте перейдём к практической части занятия.

Задача первая. Радиус основания цилиндра равен  см, высота цилиндра равна диаметру его основания. Найдите площадь боковой поверхности цилиндра.

Решение.

Задача вторая. Найдите площадь сечения цилиндра плоскостью, параллельной его оси и проходящей на расстоянии  см от неё, если площадь полной поверхности цилиндра равна  см², а площадь боковой поверхности  см².

Решение.

Задача третья. Призма со сторонами основания  см и  см и диагональю  см вписана в цилиндр. Найдите объём и площадь полной поверхности цилиндра.

Решение.

Задача четвёртая. Плоскость, параллельная оси цилиндра, отсекает от окружности основания дугу . Диагональ полученного сечения равна  и удалена от оси цилиндра на расстояние . Найдите объём цилиндра.

Решение.

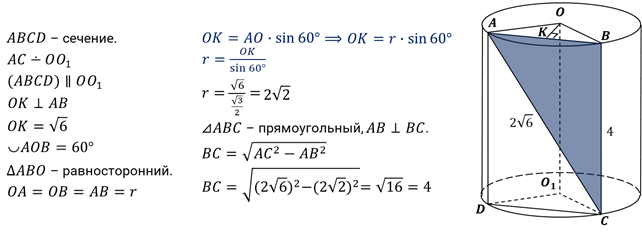
Задача пятая. В цилиндрический сосуд налили  см³ воды. Уровень жидкости оказался равным  см. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на  см. Найдите, чему равен объём детали. Ответ выразите в см³.

Решение.