Линейное уравнение с двумя переменными

Вопросы занятия:

·  повторить что такое линейное уравнение с одной переменной и сколько решений может иметь такое уравнение;

·  ввести понятия «линейное уравнение с двумя переменными», «решение уравнения с двумя переменными», «равносильные уравнения».

Материал урока

Ранее мы с вами рассматривали линейное уравнение с одной переменной.

Вспомним, что:

Сегодня на уроке мы познакомимся с линейным уравнением, но уже с двумя неизвестными.

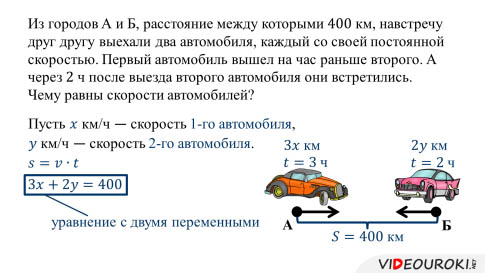
Давайте рассмотрим ситуацию

Полученное равенство содержит две переменные. А поэтому такие равенства называют уравнениями с двумя переменными (или с двумя неизвестными).

Посмотрите на примеры уравнений с двумя переменными

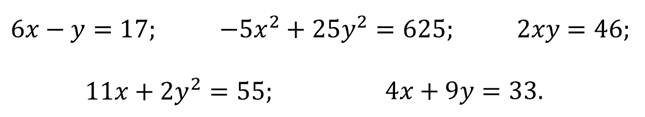
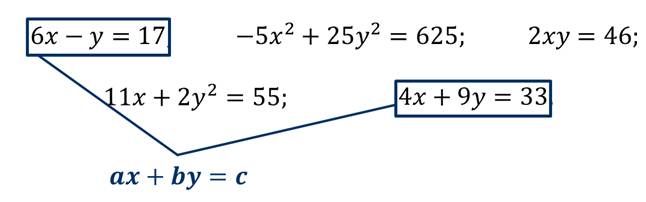
Сформулируем определение:

Определение.

Линейным уравнением с двумя переменными называется уравнение вида:

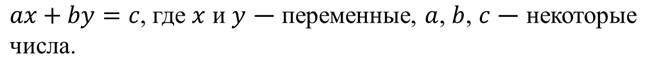
Вернёмся к задаче

То есть пара значений переменных (x = 60, y = 110) является решением этого уравнения. Отметим, что эти корни были найдены методом подбора, причём это не единственная пара чисел, удовлетворяющих нашему уравнению.

Определение.

Решением уравнения с двумя переменными называется пара значений переменных, которая обращает это уравнение в верное равенство.

Вспомним, что при изучении уравнений с одной переменной, мы говорили о равносильных уравнениях, то есть уравнениях, которые имеют одни и те же корни.

Аналогично можем сказать, что уравнения с двумя переменными, имеющие одни и те же решения, называются равносильными.

Причем уравнения с двумя переменными, не имеющие решений, также являются равносильными.

Равносильные уравнения обладают следующими свойствами:

Свойство 1.

Если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получится уравнения, равносильное данному;

Свойство 2.

Если обе части уравнения умножить (или разделить) на одно и то же отличное от нуля число, то получится уравнение, равносильное данному.

Снова вернёмся к нашему уравнению

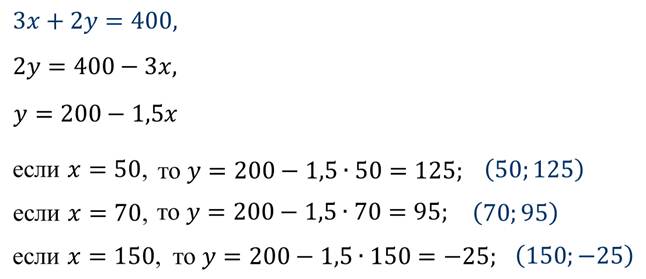
Но здесь важно знать, значение какой из переменных стоит на первом месте, а какой – на втором. Так в нашем случае сначала записано значение переменной x, а затем переменной y.

При этом пара чисел (150; - 25) являясь решением уравнения, не удовлетворяет условию задачи, так как скорость автомобиля не может быть отрицательной.

И давайте рассмотрим ещё одну задачу.

Пример.

Решение уравнений в целых числах, то есть когда надо найти только целые значения переменных, подробно рассматривал древнегреческий математик Диофант.

Поэтому уравнения с несколькими переменными, которые надо решить в целых числах, называют диофантовыми уравнениями. То есть уравнение, составленное в предыдущей задаче, является диофантовым, так как для него мы отыскивали только натуральные решения.

И давайте рассмотрим примеры.

Пример.

И ещё пример.

Пример.

Итоги урока

Итак, на этом уроке мы рассмотрели линейное уравнение с двумя переменными и один из способов решения таких уравнений.