Деление с остатком столбиком. Проверка деления с остатком

Привет, друзья! А вот и я.

Опять буду знакомить вас с новой темой. Я надеюсь, вы уже уверенно научились выполнять деление с остатком? Помните, как мы шестнадцать делили на пять?

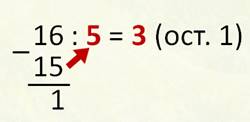
Вспоминаем таблицу умножения и деления с числом пять. Находим число, которое делится на пять без остатка и на числовом луче находится ближе остальных к числу шестнадцать. Это пятнадцать. Пятнадцать делим на пять, получается три, а разницу между шестнадцатью и пятнадцатью – один, записываем в остаток.

Вы уже знаете, что знак умножения может записываться по-разному – иногда точкой, иногда косым крестиком, а на клавиатуре компьютера или мобильного телефона – звёздочкой. Но и знак деления тоже может выглядеть по-разному: в тетрадях вы обычно пишете двоеточие, иногда этот знак выглядит как горизонтальная черта, а над ней и под ней по точке. Но для письменного деления многозначных чисел используют знак деления, который похож на лежащую на боку букву Т. И сегодня мы воспользуемся таким знаком деления для того, чтобы выполнять деление с остатком столбиком.

Вот посмотрите, допустим, нам надо разделить число двадцать пять на четыре.

Как это записать, я покажу на разлиновке в клеточку. Ведь при таком способе решения, как и при сложении и вычитании столбиком, очень важна аккуратность записи. Итак, пишу делимое – число двадцать пять. Справа от него, отступив одну клеточку, пишу делитель – четыре. Между ними ставлю знак деления – вертикальная черта длиной в две клетки, а от неё – горизонтальная. Вот она, буква Т. Вот делимое, вот делитель. Под чертой место для частного.

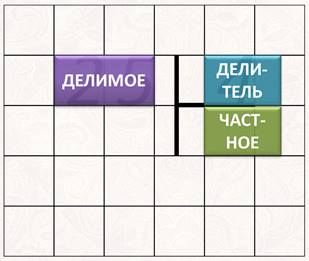
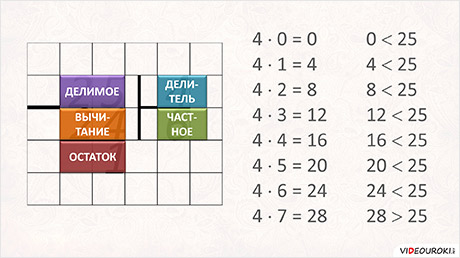
Сначала выясним, сколько раз число четыре содержится в двадцати пяти. Четыре умножаем на нуль, равно нуль. Нуль меньше двадцати пяти. Так что нуль в качестве частного нам уж точно не подходит.

Четыре умножаю на один. Четыре. Это число тоже меньше двадцати пяти и тоже нас не устраивает. Четыре умножаю на два – шесть. Оно тоже меньше двадцати пяти. Четыре умножаю на три – двенадцать, четырежды четыре – шестнадцать, четырежды пять – двадцать. Четыре умножить на шесть – двадцать четыре. На семь – двадцать восемь. А двадцать восемь не меньше, а больше двадцати пяти.

Стоп! Теперь получилось число, которое больше нашего делимого. Но это недопустимо. Возвращаемся к шестёрке. Итак, четыре содержится в числе двадцать пять шесть раз. Записываю в частном число шесть. А под делимым – то число, которое получилось при умножении делителя и частного – двадцать четыре.

А теперь вычитаю из делимого это полученное число двадцать четыре. Видите, получилось вычитание столбиком. А результат вычитания – это остаток. Я надеюсь, вы не забыли, что остаток обязательно должен быть меньше делителя. В этом примере остаток один. Он меньше четырёх. Значит, деление выполнено верно.

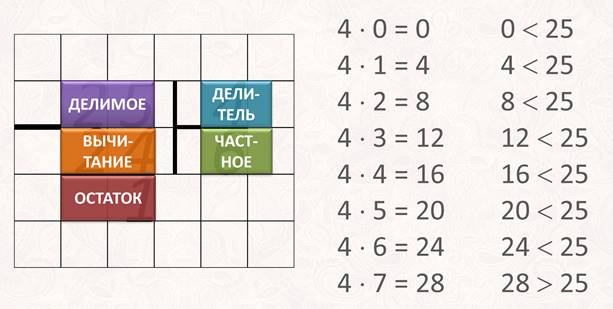
Запомните, как расположены компоненты деления. Делимое и делитель находятся на одной строчке, между ними пропускается одна клеточка. Частное расположено под делителем, а под делимым – действие вычитания и остаток.

Конечно, у нас получилось очень длинное вычисление. Методом проб и ошибок, начиная с нуля, мы нашли нужное нам число. Но, если вы хорошо знаете таблицу умножения, подбор нужного числа не будет столь долгим и утомительным.

Вот, к примеру, надо сорок пять разделить на шесть. Вспомнив таблицу умножения числа шесть, мы можем сказать, что ближайшими числами к делимому, которые делятся на шесть, являются числа сорок два и сорок восемь. Сорок восемь получится в результате умножения шести на восемь. Но число сорок восемь больше сорока пяти, и оно нам не подойдёт.

Сорок два получится в результате умножения шести на семь. Сорок два меньше сорока пяти. Значит, шесть содержится в сорока пяти семь раз. А остаток три. Наш остаток меньше делителя, значит, деление выполнено верно.

Ну а если, к примеру, надо число семь разделить на девять. Сколько раз число девять содержится в семи? Ну конечно, нуль раз. В частном записываем нуль. Нуль умножили на девять, тоже получился нуль, вычитаем... Остаток семь.

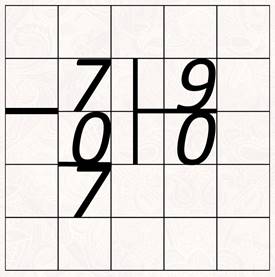
Если делимое меньше делителя, то в ответе получится нуль, а остаток будет равен делимому.

Ребята, а вы знаете, несмотря на то, что вы вроде бы всё правильно делаете, при делении с остатком случаются и ошибки. Как же проверить, правильно ли было выполнено деление?

Ну конечно обратными действиями. Мы выполняли деление и, чтобы найти остаток, вычитание. Значит, для проверки нам понадобится умножение и сложение.

Давайте сейчас разделим число сорок три на одиннадцать. Запишем решение в строчку. Сколько раз одиннадцать содержится в числе сорок три? Ну понятно, что не нуль и не один раз. Если взять два, получится число двадцать два. Оно меньше сорока трёх. Если взять три раза – это тридцать три. Оно тоже меньше сорока трёх. Возьмём число четыре – получится сорок четыре. Оно больше сорока трёх. Стоп! Возвращаемся к числу три. Число одиннадцать содержится в сорока трёх три раза и остаток десять.

Вроде бы всё правильно. Но убедиться в этом мы сможем, только выполнив проверку. Сравниваем остаток с делителем. Десять меньше одиннадцати. Это правильно. Теперь деление и вычитание проверяем умножением и сложением.

Делитель, одиннадцать, умножаем на частное, три, и к результату прибавляем остаток, десять. Одиннадцать умножить на три – тридцать три, и плюс десять – сорок три.

Ну, вроде бы всё рассказал. Ну, а если что-то по рассеянности пропустил, вам обязательно расскажет это ваш мудрый учитель.

А теперь я предлагаю вам повторить то, о чём мы сегодня говорили.

* Деление с остатком можно записывать как в строчку, так и столбиком.

* При записи столбиком делимое и делитель находятся на одной строчке, между ними пропускается одна клеточка, в которой записывается знак деления, похожий на букву Т, лежащую на боку. Частное расположено под делителем, а под делимым – действие вычитания и остаток.

Если делимое меньше делителя, то в ответе получится нуль, а остаток будет равен делимому.

Деление с остатком можно проверить.

1. Для этого сначала сравниваются остаток с делителем.

Важно! Остаток должен быть меньше делителя!

После сравнения остатка с делителем выполняем второй этап проверки.

2. Умножить частное на делитель и к полученному произведению прибавить остаток.

Ну вот и пришло время нам сегодня попрощаться. Хороших вам отметок, ребята! До свидания!