В мире математики

Сегодня на занятии мы будем выполнять самые разные задания. Это будут задания, для решения которых нам пригодятся не только знания, но и смекалка.

Давайте сразу приступим к выполнению заданий.

Задание первое. Ученик переписал числовое выражение, значение которого равно 58, но забыл поставить скобки.

У него получилось вот такое выражение:

6 · 8 + 20 : 4 – 2

Где в этом выражении должны стоять скобки?

Решение.

Задание второе. В пустые клетки данного квадрата размером 3 на 3 необходимо вставить числа 1, 4, 5, 6, 7, 8 так, чтобы квадрат стал магическим.

Напомним, что магические квадраты – это квадраты, разбитые на определённое количество клеток, в которые вписаны числа. При этом числа расположены так, что суммы чисел вдоль каждого горизонтального ряда, каждого вертикального столбца, а также каждой из двух диагоналей всегда одинаковы.

Решение. В первую очередь найдём сумму всех чисел, которые должны быть размещены в клетках квадрата.

1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45

Это сумма чисел, которые уже записаны в клетках квадрата и которые даны в условии задачи.

Получается, что сумма всех чисел – 45. Она складывается из сумм в каждом ряду.

В квадрате 3 ряда и сумма чисел в каждом ряду одинакова.

45 : 3 = 15

Это число будет магической константой нашего квадрата.

М = 15

Константа – это постоянная, не изменяющаяся величина. В данном случае константой является одинаковая сумма чисел в каждом столбике, в каждой строчке и в каждой диагонали.

Итак, найдём число, которое должно стоять вот в этой клетке…

Теперь найдём число, которое должно стоять в этой клетке квадрата…

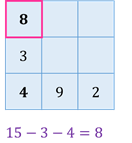
У квадрата есть две диагонали. Сумма чисел вдоль них также равна 15. Посмотрите на числа, стоящие вдоль одной из диагоналей. Неизвестно только одно число.

Найдём его…

Далее посмотрите на числа, которые стоят вдоль другой диагонали. Также неизвестно только одно число.

Найдём это число…

Теперь найдём число, которое должно стоять в средней клетке верхнего ряда…

И осталось найти ещё одно число…

Вот таким образом, мы вписали данные числа в квадрат так, что он стал магическим.

Задание третье. Установите закономерность в расположении чисел каждого ряда и допишите в соответствии с этой закономерностью ещё два числа.

Решение.

Задание четвёртое. 16 спичек выложены так, как показано на рисунке. Переложите 4 спички так, чтобы получилось 3 квадрата.

Решение.

Первый способ.

У нас получилось два квадрата с длиной стороны, равной двум спичкам, и один квадрат с длиной стороны, равной одной спичке. Всего – три квадрата.

Отметим, что начать перемещение спичек можно с любого угла большого квадрата.

Второй способ.

Получили три квадрата. Это два квадрата с длиной стороны, равной одной спичке, и квадрат с длиной стороны, равной трём спичкам.

Обратите внимание, что спички, из которых составлен маленький квадрат, можно было переложить и так…

При этом в каждом из вариантов получается три квадрата: два маленьких и один большой.

Следующее задание. Составьте фигуры, изображённые на рисунке, из фигурок пентамино.

С пентамино (известной логической игрой и головоломкой) мы познакомились на одном из наших занятий. Напомним, что набор пентамино содержит 12 фигурок, каждая из которых составлена из 5 одинаковых квадратов, причём квадраты «соседствуют» друг с другом только сторонами. Все элементы обозначаются латинскими буквами, форму которых они напоминают.

Решение.

Выполним ещё одно задание. Составьте картинку, изображённую на рисунке, из 7 частей танграма.

Вспомним, что танграм – это занимательная головоломка. Она получается, если взять квадрат размером 6 на 6 клеток и разрезать его на части вот таким образом…

Здесь 7 элементов. 2 больших треугольника, 2 маленьких и 1 средний. А также 2 четырёхугольника, один из которых – квадрат.

Решение. Давайте нижнюю часть собачки сложим из двух больших треугольников и одного среднего. Головой собачки будет квадрат. А ушами – маленькие треугольники. Хвостом собачки будет оставшийся четырёхугольник.