Связь между компонентами и результатом действия умножения

- Добрый день, мои дорогие ребята. Сегодня я расскажу вам о том, как связаны между собой компоненты и результат действия умножения. Вы спросите, почему я, а не полюбившиеся вам Плюс и Минус? Дело в том, что они прекрасно разбираются в сложении и вычитании, но вот действия умножения и деления им даются не очень хорошо. А их родственники Умножение и Деление ещё маловаты для того, чтобы что-то вам объяснять. Им и самим надо ещё учиться и учиться.

Ну что же, приступим.

Я предлагаю вам посмотреть на эти кубики.

Вы помните, с ними играли Плюс и его братик Умножение. Малыш Умножение построил вот такую стеночку из кубиков. Сейчас мы узнаем, сколько всего кубиков понадобилось для этой стенки. В ней по 3 кубика каждого цвета, и были использованы кубики 5 разных цветов. То есть, можно сказать, что брали по 3 кубика 5 раз. А математическая запись при этом выглядит так:

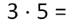
Но, чтобы написать ответ, нам необходимо вспомнить, что обозначает каждый из множителей. Вы же помните, что действие умножение заменяет действие сложение, когда слагаемые одинаковые.

В действии умножения первый множитель показывает, какие числа складываем, второй множитель показывает, сколько их. В нашем действии надо по 3 взять 5 раз:

Значит, и в действии умножения ответ - 15:

Я надеюсь, вы не забыли, что он называется произведением. Ну а теперь мы приступим к основной теме - связь между компонентами и результатом действия умножения.

Мы с вами решили задачу, в которой было известно, сколько кубиков составляют один ряд, и сколько таких рядов. А надо было узнать, сколько всего кубиков.

А теперь решим обратную задачу. Вы же помните - в обратной задаче неизвестное число становится известным, а одно из известных становится неизвестным.

Итак, у нас 15 кубиков, из которых сложена стенка. Мы видим, что кубики располагаются горизонтальными рядами разного цвета по 3 кубика в каждом ряду.

Сейчас мы будем узнавать, сколько таких рядов? Так как в каждом ряду кубиков поровну, то получим:

Ответ: 5 рядов.

Ну, и ещё одна обратная задача. Для того чтобы построить стенку, взяли 15 кубиков и поставили их в 5 рядов. По сколько кубиков получилось в каждом ряду?

Получаем:

Ну вот, мы и решили 3 задачи. А сейчас я хочу обратить ваше внимание на запись решения этих задач. Вот решение первой задачи, выполненное действием умножения. В нём первый множитель - 3, второй множитель - 5, произведение равно 15.

А теперь посмотрите на решение второй задачи. Если вы внимательно посмотрите, то заметите, что здесь произведение из первой задачи разделили на первый множитель, и получили второй множитель.

А в третьей задаче произведение разделили на второй множитель и получили первый множитель.

Вы видите, как между собой связаны множители и произведение?

Запомните, ребята.

Если произведение двух множителей разделить на один из них, то получится другой множитель.

Давайте разберём ещё одну задачу. Если вы помните, Плюс с братиком Умножением построили 2 гаража, и в каждый поставили по 7 машинок. Сколько всего машинок было в двух гаражах?

Эта задача решается действием умножения. Находим произведение чисел 7 и 2:

Ответ: 14 машинок.

А теперь составляем обратную задачу. Плюс и Умножение поставили 14 машинок поровну в 2 гаража. По сколько машинок стоит в каждом гараже?

Эту задачу решаем действием деления. Нужно 14 разделить на 2 получаем…Помните? Если произведение двух множителей разделить на один из них, то получится другой множитель. 14 - это произведение чисел 7 и 2 Значит, получаем:

Ответ: 7 машинок.

Ну и ещё одна обратная задача.

Плюс и Умножение решили, поставили 14 машинок в гаражи по 7 машинок в каждый гараж. Сколько гаражей понадобится для этого?

Нужно 14 разделить на 7, получается.... Если 14, это произведение чисел 7 и 2, тогда получаем:

Ответ: понадобиться по 2 гаража.

Ну что, ребята, вы поняли, как связаны между собой множители и произведение?

Давайте для закрепления запишем вот такой пример:

А теперь составим из него два примера на деление. Произведение станет делимым, а множители, по очереди, делителями. Получаем:

Ну вот и пришла пора нам с вами прощаться. Я надеюсь, вы никогда не забудете, что если произведение двух множителей разделить на один из них, то получится другой множитель.

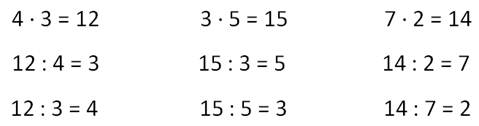
До свидания, ребята! Успехов вам!