Принцип Дирихле

Давайте представим, что у нас есть 4 зайца, которые не дружат друг с другом и постоянно дерутся. Мы хотим посадить их в клетки, чтобы, наконец, они успокоились и им не с кем было бы драться. Удастся ли это сделать, если у нас есть только 3 клетки?

Конечно, нет, так как в одну из клеток нужно будет посадить не меньше 2 зайцев – и драки не избежать.

Так получилось, потому что клеток меньше, чем зайцев.

Также мы не сможем посадить 7 зайцев в 3 клетки, чтобы в каждой было не больше 2 зайцев. В одну из клеток придётся посадить 3 зайца.

Такие подсчёты с зайцами и клетками связаны с математическим утверждением – принципом Дирихле.

Сформулируем этот принцип так: если зайцы рассажены в клетки, причём количество зайцев больше количества клеток, то хотя бы в одной из клеток находится больше одного зайца.

Задачи, в которых используется принцип Дирихле, называют задачами на принцип Дирихле. При решении таких задач важно понять, что является «зайцем», а что служит «клеткой».

Давайте решим несколько задач.

Задача первая. В спортивном лагере 22 человека. Можно ли утверждать, что среди них найдутся хотя бы 2, имена которых начинаются с одной и той же буквы?

Решение.

А можно ли утверждать, что среди 35 учеников класса обязательно найдутся 2 ученика, фамилии которых начинаются с одной и той же буквы?

Можно, ведь в алфавите только 33 буквы. Причём есть буквы, на которые фамилия начинаться не может.

Задача вторая. В школе 400 учеников. Почему среди учащихся этой школы обязательно найдутся 2 ученика, родившиеся в один день?

Решение.

Задача третья. В школе 735 учащихся. Можно ли утверждать, что по крайней мере 3 ученика должны отмечать день своего рождения в один и тот же день?

Решение.

Задача четвёртая. Работая в школьном саду на уборке урожая фруктов, школьники собрали 22 ящика, в одних из которых – яблоки, в других – груши, в третьих – сливы. Можно ли утверждать, что имеется по крайней мере 8 ящиков, содержимое которых составляет один из указанных видов фруктов?

Решение.

Решим следующую задачу. В школе 33 класса, 1150 учеников. Найдётся ли в этой школе класс, в котором не менее 35 учащихся?

Решение.

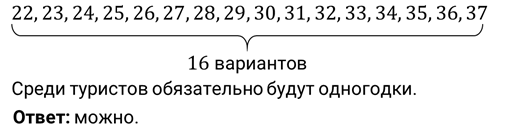
И решим ещё одну задачу. В поход пошли 20 туристов. Самому старшему из них 37 лет, а самому младшему 22 года. Можно ли утверждать, что среди туристов есть одногодки?

Решение.