Независимые события

В повседневной жизни мы часто сталкиваемся с ситуациями, когда события каким-то образом связаны между собой. То есть по наступлению одного события можно судить об изменении вероятности другого. Например, если небо ясное, то мы считаем вероятность дождя небольшой. Но если вдруг сгустились тучи, то мы заново оцениваем ситуацию и считаем, что вероятность дождя теперь высокая.

Если мы бросаем игральный кубик, то вероятность того, что выпадет 2 очка, равна . Вероятность того, что выпадет 6 очков, тоже равна . Если же нам сказали (но мы этого сами не видели), что выпало больше 3 очков, то выпадение 2 очков стало невозможным событием (условная вероятность этого стала равна 0), а вероятность выпадения 6 очков выросла до .

Бывают события, которые не зависят друг от друга. Например, при бросании двух монет результат бросания первой монеты не влияет на результат бросания второй монеты. Про такие события говорят, что они независимы.

Можно считать, что события  и  независимы, если наступление одного из них не влияет на вероятность другого.

Если вероятности событий  и  больше 0, то независимость событий  и  можно выразить равенствами: . Тогда из известных нам формул  и  получается равенство 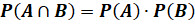. Возьмём это равенство за определение независимости двух событий.

Два события  и  называются независимыми, если вероятность их пересечения равна произведению их вероятностей.

Аналогично можно говорить о независимости трёх, четырёх и более событий. Если вероятность пересечения любого набора этих событий равна произведению их вероятностей, то события называются независимыми.

Часто независимые события возникают, когда случайный эксперимент состоит из нескольких независимых случайных испытаний.

Пример. Игральный кубик бросают 2 раза. Событие  – «в первый раз выпало меньше 4 очков», событие  – «во второй раз выпало больше 4 очков». Будут ли события  и  независимыми?

Изобразим результаты этого случайного эксперимента с помощью таблицы размером 6 на 6 клеточек, где номер строки – результат первого броска, а номер столбца – результата второго броска.

Событие  состоит в том, что в первый раз выпало меньше 4 очков. Выделим в таблице это событие зелёным цветом.

Событие  состоит в том, что во второй раз выпало больше 4 очков. Выделим в таблице это событие синим цветом.

Общее число элементарных событий рассматриваемого случайного эксперимента равно 36. Событию  благоприятствуют 18 элементарных событий. Событию  благоприятствуют 12 элементарных событий. Пересечению событий  и  благоприятствуют 6 элементарных событий.

Получается, что 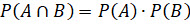, а значит, события  и  независимы.

Следует отметить, что независимые события встречаются не только при независимых испытаниях.

Пример. Случайным образом выбираем натуральное число от 1 до 100. Пусть событие  – «выбранное число чётное, событие  – «выбранное число делится нацело на 5».

Покажем, что события  и  независимы. Для этого нужно найти вероятность события , вероятность события , вероятность пересечения событий  и , а затем убедиться, что выполняется равенство .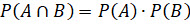

Среди 100 первых натуральных чисел всего 50 чётных чисел и 25 чисел, которые делятся нацело на 5.

Поэтому 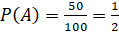, . Тогда .

Пересечение событий  и  состоит в том, что выбранное число делится нацело и на 2, и на 5, то есть оно делится нацело на 10.

Среди первых 100 натуральных чисел всего 10 чисел, которые делятся нацело на 10. Следовательно, .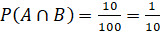

Видим, что вероятность пересечения событий  и  равна 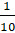 и произведение вероятностей событий  и  равно 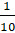. Получается, что известное нам равенство выполняется. Значит, события  и  независимы.

Не следует путать независимые и несовместные события. Несовместные события, как правило, зависимы: если произошло одно из них, то мы заведомо знаем, что не произошло другое.

Чаще о независимости событий судят не по тому, выполняется или нет данное равенство, а по тому, как устроен случайный эксперимент, в котором эти события наступают.

Выполним несколько заданий.

Задание первое. События  и  независимы. Чему равна вероятность пересечения событий  и , если , ?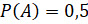

Решение.

Задание второе. События  и  независимы. Чему равна вероятность события , если , ?

Решение.

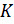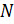Задание третье. События ,  и  независимы. Найдите вероятность пересечения этих событий, если , , .

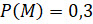Решение.

Задание четвёртое. Игральный кубик бросают 2 раза. Являются ли независимыми данные события?

Решение.

Задание пятое. Бросают игральный кубик. Событие  – «выпадет нечётное число очков». Событие  – «выпадет число очков, кратное 3». Являются ли независимыми события  и ?

Решение.

До встречи на следующих занятиях!