Дерево случайного опыта

Пример. Рассмотрим случайный эксперимент, в котором монету бросают 2 раза. Возможные события этого эксперимента будем изображать с помощью дерева.

Начальную вершину дерева обозначим буквой S (это состояние, когда ни один бросок ещё не сделан). От этой вершины проведём вниз два ребра к вершинам, которые обозначим буквами О и Р. Эти вершины изображают события «орёл» и «решка» при первом броске.

Около рёбер запишем вероятности этих событий. Они равны , ведь математическая монета считается симметричной, то есть имеет равные шансы выпадения орла или решки.

Затем от каждой из вершин проведём ещё по 2 ребра к событиям, которые могут случиться при втором броске. Около рёбер запишем вероятности событий.

Мы построили дерево случайного эксперимента, в котором монету бросают 2 раза.

Запомните, что при построении дерева случайного эксперимента нужно следить, чтобы сумма вероятностей около всех рёбер, выходящих из одной вершины, была равна 1.

Обратите внимание на одно из рёбер построенного дерева.

Около него указана вероятность. Она равна . Это условная вероятность события «выпало два орла» при условии, что в первый раз выпал орёл.

Получается, около рёбер в дереве случайного эксперимента подписываются условные вероятности.

Если дерево случайного опыта конечное, то элементарные события в дереве случайного опыта изображаются цепями, ведущими из начальной вершины к конечным вершинам дерева.

Например, элементарное событие «выпало две решки» изображено цепью, которая выделена зелёным цветом.

Найти вероятность элементарного события можно с помощью правила умножения вероятностей: нужно найти произведение условных вероятностей вдоль соответствующей цепи.

Чтобы найти вероятность события «выпало две решки», нужно умножить вероятности вдоль соответствующей цепи.

Не элементарные, а более сложные события изображаются промежуточными вершинами дерева или какой-нибудь фигурой (например, овалом), объединяющей благоприятствующие элементарные события.

Пример. На рисунке изображено дерево некоторого случайного эксперимента, в котором 4 элементарных события:  и .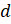

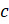Случайное событие  показано овалом, который объединяет элементарные события  и .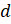

Промежуточная вершина 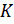 изображает другое событие, которому благоприятствуют элементарные события  и .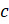

Найдём вероятности событий  и .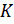

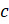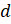Событию ЭМ благоприятствуют элементарные события  и . Значит, нужно найти сумму вероятностей соответствующих цепей.

Событию 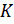 благоприятствуют 3 элементарных события. Но нам не нужно искать вероятности всех трёх цепей, ведь три ветки, ведущие к вершинам  и 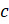, «растут» из ребра 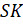, которое имеет вероятность 0,3.

Сформулируем общее правило нахождения вероятностей событий с помощью дерева, которое получается из правила сложения вероятностей несовместных событий.

Чтобы найти вероятность события с помощью дерева, нужно сложить вероятности всех цепочек, ведущих к этому событию от начальной вершины.

Дерево позволяет рассматривать случайный эксперимент по частям, мысленно расположив случайные события в некотором порядке. Но так как очерёдность эта только мысленная, то при желании её можно поменять.

Деревья очень удобны при решении задач, связанных со случайным выбором.

Задача. В классе 9 девочек и 11 мальчиков. Случайным образом из класса выбирают двух человек. Какова вероятность того, что будут выбраны одна девочка и один мальчик?

Решение.

Изобразим дерево случайного эксперимента, мысленно разбив одновременный выбор случайной пары на два последовательных выбора.

Обозначим буквой S начальную вершину. От этой вершины проведём вниз 2 ребра. Выбор девочки обозначим буквой Д, а выбор мальчика – буквой М.

Известно, что классе 9 девочек и 11 мальчиков. Тогда всего в классе 20 человек.

При первом выборе вероятность выбрать девочку равна 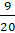, а мальчика – 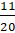. Укажем эти вероятности около соответствующих рёбер.

При выборе второго ребёнка вероятности появления девочки и мальчика зависят от того, кто был выбран в первый раз.

Если в первый раз была выбрана девочка, то осталось 8 девочек из 19 человек. Поэтому во второй раз девочка будет выбрана с вероятностью 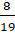, а мальчик будет выбран с вероятностью .

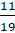Если в первый раз был выбран мальчик, то осталось 10 мальчиков из 19 человек. Поэтому во второй раз мальчик будет выбран с вероятностью , а девочка будет выбрана с вероятностью .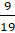

Событию А «выбраны одна девочка и один мальчик» благоприятствуют 2 элементарных события. Они изображены в дереве цепочками, которые выделены зелёным цветом.

Чтобы найти вероятность события А, сложим вероятности цепочек, ведущих к этому событию от начальной вершины дерева.

Выполним несколько заданий.

Задание первое. На рисунке изображено дерево некоторого случайного эксперимента. Вычислите вероятности данных цепочек.

Решение.

Чтобы выполнить это задание, надо найти произведение условных вероятностей вдоль каждой из данных цепей.

Задание второе. На рисунке изображено дерево некоторого эксперимента и событие N. Рёбра проведены пунктиром. Известно, что рёбра, исходящие из одной вершины, равновероятны. Укажите около рёбер соответствующие вероятности. Обведите сплошной линией цепочки, благоприятствующие событию N. Найдите вероятность события N.

Решение.

До встречи на следующих занятиях!