В прошлой теме говорилось о том, что такое механическая волна.
Механическая волна – это колебание, которое распространяется с течением времени в упругой среде.
Все волны делятся на два вида — продольные и поперечные. Волна называется поперечной, если частицы среды совершают колебания в направлении, перпендикулярном к направлению распространения волны. Такие волны могут распространяться в любых средах.
Волна называется продольной, если частицы среды совершают колебания в направлении распространения волны. Продольные волны могут существовать только в твердых средах.
Рассмотрим более подробно процесс передачи колебаний от точки к точке при распространении поперечной волны. Для этого разберем различные стадии процесса распространения поперечной волны через каждые четверть периода.
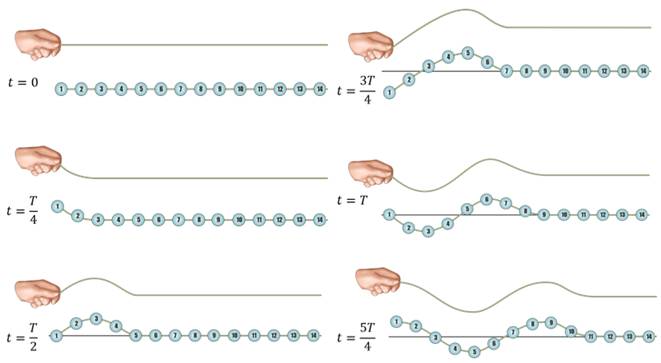
Установка представляет собой цепочку пронумерованных шариков, которые символизируют частицы среды. Будем считать, что между шариками, как и между частицами среды, существуют силы взаимодействия.
При смещении точки 1, возникнут силы упругости, которые заставят точку 2 двигаться вслед за точкой один. Это приводит к возникновению сил упругости между точками 2 и 3 и т.д.
Таким образом, благодаря силам взаимодействия каждый шарик в цепочке будет повторять движение первого, но с некоторым запаздыванием. Это запаздывание будет тем больше, чем дальше от первого шарика находится данный шарик.
За вторую четверть периода точка 1 вернется в положение равновесия. Точка 3 испытает максимальное отклонение, а точка 5 только начнет движение.
К концу третьей четверти периода точка 1 испытает максимальное отклонение вниз, точка 3 будет проходить положение равновесия, точка 5 испытает максимальное отклонение вверх, а точка 7 только начнет движение.
К концу периода точка 1 завершит полное колебание и снова придет в положение равновесия, точка 3 отклонится на амплитудное значение вниз, точка 5 будет проходить положение равновесия, точка 7 отклонится на амплитудное значение вверх, а точка 9 только начнет движение.
Еще через четверть периода точки 1 и 9 уже будут колебаться одинаково. Таким образом, за время равное периоду колебаний, волна распространяется от точки 1 до точки 9.
Каждый шарик в отдельности будет совершать колебательное движение. А все вместе эти колебания будут представлять собой поперечную волну.
Раз это колебание, то волне будут присущи все характеристики, которые соответствуют колебанию: амплитуда, период колебания и частота.
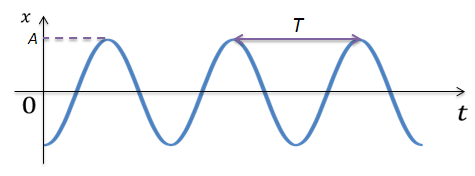
Амплитуда — это максимальное смещение тела от положения равновесия.
Промежуток времени, в течение которого тело совершает одно полное колебание, называется периодом.
Число колебаний в единицу времени называется частотой колебаний.
Кроме этого возмущение, создаваемое колеблющимся в упругой среде телом, передается от одной точки среды к другой. Это происходит не мгновенно, а с определенной скоростью. Скоростью распространения волны называется физическая величина, определяемая расстоянием, которое проходит любая точка фронта волны за единицу времени. Вектор скорости направлен по нормали к волновой поверхности в сторону распространения волны и в однородной среде совпадает с направлением луча. Следует отличать скорость распространения волны от скорости колебания частиц среды около своих положений равновесия.
Пусть волна распространяется вдоль горизонтальной оси (например, вдоль упругого горизонтального шнура). В данный момент времени форма волны повторяется в пространстве вдоль шнура через определенные отрезки. На рисунке показан профиль волны в определенный момент времени.
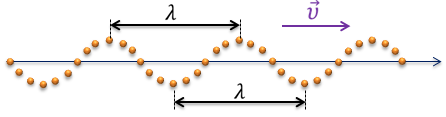
Расстояние между ближайшими точками, колеблющимися в одинаковых фазах, называется длиной волны. Длина волны обозначается греческой буквой l (лямбда). Онаравна расстоянию, на которое распространяется фронт волны за время, равное периоду колебаний источника волн:

Так как период и частота связаны соотношением:
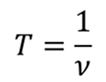
то скорость волны связана с частотой колебаний уравнением:
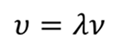
Отсюда
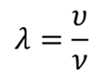
Тогда смещение точки среды с координатой r в момент времени t равно

Это и есть уравнение плоской бегущей монохроматической волны (при этом предполагают, что затуханием волны в процессе ее распространения можно пренебречь). Смещение любой точки среды из равновесного положения при прохождении волны является функцией двух переменных: времени и расстояния до равновесного положения точки среды.
Основные выводы:
– Волне присущи все характеристики, которые соответствуют колебанию: амплитуда, период колебания и частота. Кроме этого возмущение, создаваемое колеблющимся в упругой среде телом, передается от одной точки среды к другой. Это происходит с определенной скоростью.
– Скорость распространения волны — это физическая величина, определяемая расстоянием, которое проходит любая точка фронта волны за единицу времени. Вектор скорости направлен по нормали к волновой поверхности в сторону распространения волны и в однородной среде совпадает с направлением луча.
– Расстояние между ближайшими точками, колеблющимися в одинаковых фазах, называется длиной волны.
– Уравнение плоской бегущей монохроматической волны:


 Получите свидетельство
Получите свидетельство Вход
Вход




 0
0 6363
6363

