Сегодня на занятии рассмотрим логические задачи, при решении которых удобно применять так называемые круги Эйлера.
Леонард Эйлер был выдающимся учёным. Жил он в XVIII веке. Эйлер внёс огромный вклад в развитие физики, математики, астрономии и других наук. Его именем названы более 20 математических формул. В день 200-летия со дня рождения этого великого математика было издано на его родине, в Швейцарии, всё его наследие, которое состояло из 72 томов по 600 страниц.
Ну а что это за круги Эйлера, вы увидите вот на таком примере.
Пусть, например, А – множество отличников в классе, а Б – множество спортсменов в этом же классе.
Нарисуем круг, который изображает множество А. Нарисуем круг, который изображает множество Б. Тогда общая часть этих кругов изображает отличников, которые занимаются спортом.

Отметим, что иногда вместо кругов для изображения множеств применяют фигуры другой формы, например, овалы.

Применение кругов Эйлера при решении некоторых видов задач придаёт им наглядность и простоту.
Давайте решим такую задачу. У всех друзей Миши есть домашние питомцы. 7 друзей любят и держат кошек, а 5 – собак. И только у 3 есть и кошка, и собака. Сколько у Миши друзей?
Решение.

Решим следующую задачу. 35 шестиклассников являются читателями школьной и районной библиотек. Из них 25 берут книги в школьной библиотеке, 20 – в районной. Сколько учеников не являются читателями районной библиотеки?
Решение.

Можно узнать, сколько учеников посещают только районную библиотеку.

Следующая задача. Сколько в классе учащихся, если известно, что лыжным спортом увлекаются 28 человек, отличников в классе 12, причём отличников-спортсменов, увлекающихся лыжами, 10 человек?
Решение.

Отметим, что правильнее будет сказать, что в классе не менее 30 учеников, ведь могут быть ученики, которые не являются ни лыжниками, ни отличниками.
Решим такую задачу. Известно, что из всех учеников класса художественную школу посещают 10 человек. Музыкальную школу – 8 человек. Спортивную школу – 12 человек. Две школы, художественную и музыкальную, – 3. Две школы, музыкальную и спортивную, – 2. Две школы, художественную и спортивную, – 2. Все три школы посещает 1 человек. Сколько учеников посещают только одну школу?
Решение.


 Получите свидетельство
Получите свидетельство Вход
Вход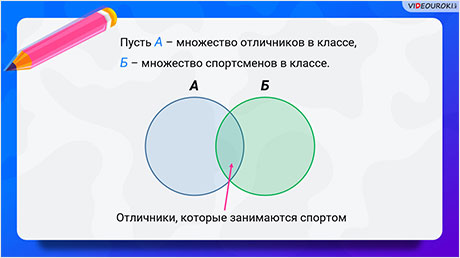




 3234
3234

