Посмотрите на эту фигуру:
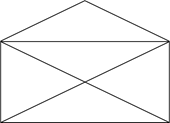
Она похожа на открытый конверт.
Наверное, многие из вас раньше пробовали нарисовать такой конверт, не отрывая карандаш от бумаги и не проводя больше одного раза по одной и той же линии.
У кого-то это получалось, а у кого-то – нет.
Вообще, эту фигуру можно нарисовать одним росчерком, если проводить линии, например, вот в такой последовательности.
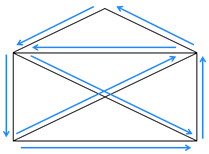
Обратите внимание, что не было проведено дважды ни по одной из линий фигуры.
А теперь посмотрите вот на такую фигуру:
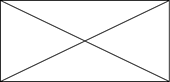
Эта фигура напоминает закрытый конверт.
На первый взгляд данная фигура кажется более простой, ведь она содержит меньше линий. Но вот нарисовать её, не отрывая карандаш от бумаги и не проводя никакой линии дважды, у нас не получится.
Почему какие-то фигуры получается нарисовать, не отрывая карандаш от бумаги и не проводя никакую линию больше одного раза, а какие-то – нет?
Давайте разберёмся. Посмотрите на рисунок, который создан при помощи нескольких линий. Такие рисунки ещё называют графами.
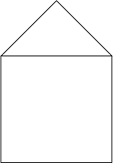
Вы, наверное, слышали, что словом «граф» называют богатого и знатного человека в старинных романах. Однако в математике граф – это рисунок, созданный при помощи прямых линий, образующих углы.
«Граф» в переводе с греческого означает «пишу». Точки, в которых соединяются линии графа, называются узлами.

В нашем графе пять узлов.
Посмотрите, в первом, втором и третьем узлах соединяется по 2 линии. То есть чётное число. Поэтому эти узлы называются чётными.
А вот в четвёртом и пятом узлах соединяется по 3 линии. То есть нечётное число. Поэтому эти узлы называются нечётными.
Получается, что в этом графе 3 чётных узла и 2 нечётных.
Попробуем нарисовать данную фигуру одним росчерком, то есть, не отрывая карандаш от бумаги и не проводя никакую линию дважды.
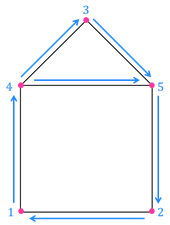
Получилось.
Теперь посмотрите на фигуру, которая похожа на домик с дверью.
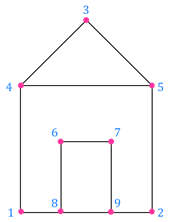
В первом, втором, третьем, шестом и седьмом узлах соединяется по 2 линии. А значит, эти узлы являются чётными.
В четвёртом, пятом, восьмом и девятом узлах соединяется по 3 линии. А значит, эти узлы являются нечётными.
Получается, что в этом графе 5 чётных узлов и 4 нечётных.
Надо отметить, что нечётных узлов здесь больше двух.
Запомните! Если в фигуре (на графе) число нечётных узлов больше двух, то её нельзя нарисовать одним росчерком.
Значит, фигуру в виде домика с дверью нельзя нарисовать одним росчерком. Ведь у этой фигуры целых 4 нечётных узла.
А сейчас давайте выполним несколько заданий.
Задание первое. Выясните, какие из фигур можно вычертить, не отрывая карандаш от бумаги и не проводя больше одного раза по одной и той же линии.
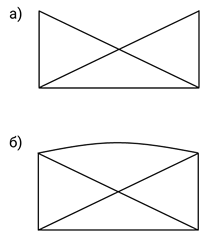
Решение.

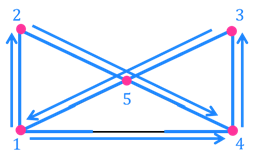

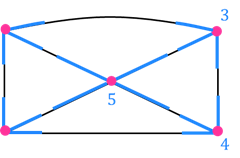
А догадался ли кто-нибудь из вас, что те фигуры, которые можно нарисовать одним росчерком, можно сделать и сгибанием из одного куска проволоки?
Задание второе. Можно ли из одного куска проволоки получить фигуру, которая изображена на рисунке?
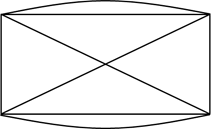
Решение.

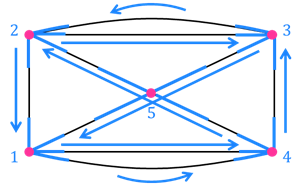
Задание третье. Выясните, можно ли нарисовать фигуру, которая изображена на рисунке, не отрывая карандаш от бумаги и не проводя более одного раза ни одной линии.

Решение.



 Получите свидетельство
Получите свидетельство Вход
Вход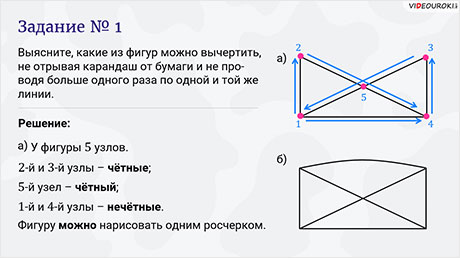




 7303
7303

