Свойства скалярного произведения векторов

Вам уже известно определение скалярного произведения векторов и правило его вычисления.

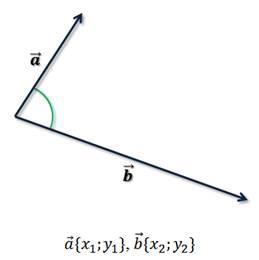
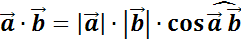
Кроме этого вы знаете, что скалярное произведение можно находить ещё и в координатах.

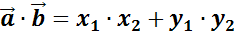
Сегодня будем говорить о свойствах скалярного произведения векторов.

Запишем первое свойство. Скалярный квадрат всегда является числом неотрицательным     .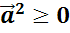

Действительно, ведь скалярный квадрат вектора равен квадрату его длины. А значит, он больше либо равен нулю.

Причём скалярный квадрат положителен, если вектор ненулевой, и равен нулю, если вектор нулевой.

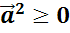
Второе свойство называют переместительным законом. Скалярное произведение векторов  равно скалярному произведению векторов  :  .

Пользуясь определением скалярного произведения, это не трудно доказать.

Что и требовалось доказать.

Третьим свойством запишем распределительный закон .

, ,

Что и требовалось доказать.

Четвёртым свойством запишем сочетательный закон .

, ;

Что и требовалось доказать.

Итак, мы доказали четыре свойства скалярного произведения векторов. Рассмотрим несколько задач, в которых можно применить данные свойства.

Задача. Найти значение выражений, если , , .

а)

б)

в)

г)

Решение.

а)

б)

в)

г)

Задача. Найти , если , .

, , , .

Решение.

А теперь рассмотрим геометрические задачи, которые решаются с применением скалярного произведения векторов.

Задача. Найти величину  в , если , , .

Решение.

Ответ: .

Задача.  квадрат, где  середина , а  середина . Доказать, что .

Доказательство.

,        ,

Итак, найдём каждую координату данных векторов как разность соответствующих координат их конца и начала.

Найдём скалярное произведение этих векторов.

Что и требовалось доказать.

Подведём итоги нашего урока.

Сегодня Вы познакомились со свойствами скалярного произведения векторов. Мы рассмотрели примеры их применения при выполнении различных заданий. В том числе убедились, что скалярное произведение векторов иногда очень удобно применять при решении геометрических задач.