Уравнение состояния идеального газа

На прошлых уроках мы с вами рассмотрели идеальный газ с позиций молекулярно-кинетической теории. И выяснили, как зависит давление идеального газа от концентрации его молекул и температуры.

Однако состояние макроскопической системы считается полностью определённым, если известны все её макроскопические параметры — давление, температура и объём. Поэтому нам необходимо установить, как связаны между собой эти макроскопические параметры.

Уравнение, связывающее температуру, давление и объем идеального газа в состоянии теплового равновесия, называют уравнением состояния идеального газа. Несмотря на то, что это уравнение было получено экспериментально, его легко можно вывести из основного уравнения МКТ:

p = nkT.

Как известно, концентрация газа — это число молекул газа в единице объёма:

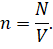
Тогда мы можем записать, что давление газа прямо пропорционально температуре и числу молекул и обратно пропорционально его объёму:

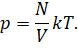
Теперь давайте соберём в левой части уравнения все макропараметры газа: его давление, объём и температуру:

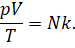
Обратите внимание на правую часть записанного равенства: «Ка» (k) — это постоянная Больцмана, а N — число молекул газа, которое при неизменной массе газа тоже является величиной постоянной. Поэтому правая часть уравнения является константой. Отсюда следует, что при неизменной массе и неизменном химическом составе газа отношение произведения его давления и объёма к абсолютной температуре является величиной постоянной:

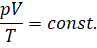
Это и есть уравнение состояния идеального газа. Впервые оно было получено французским физиком Бенуа Клайпероном в 1834 году, поэтому его называют уравнением Клайперо́на.

В справедливости уравнения можно убедиться на таком опыте. Возьмём гофрированный сосуд, объём которого можно менять при помощи винта. Объём газа измеряется с помощью линейки, а давление — при помощи манометра, подключённого к сосуду. Температура газа в сосуде равна температуре окружающей среды и может быть измерена термометром.

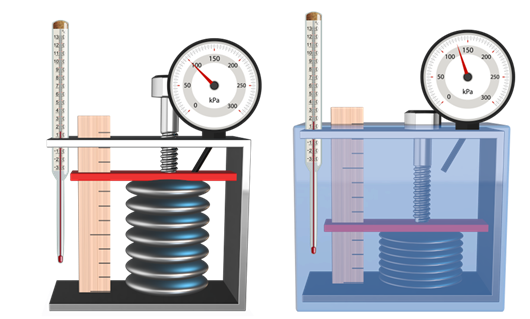
Теперь при помощи винта изменим объём сосуда. А сам сосуд поместим в горячую воду, тем самым изменив температуру газа и его давление. Дождёмся теплового равновесия.

Нетрудно заметить, что в пределах погрешности эксперимента отношение произведения давления и объёма газа к абсолютной температуре действительно является постоянной величиной:

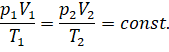
Реальные газы тоже можно описать при помощи уравнения состояния. Но для этого необходимо выполнение двух условий. Во-первых, давление газа должно быть таково, чтобы собственный объём всех молекул газа был пренебрежимо мал по сравнению с вместимостью сосуда, в котором находится газ. А во-вторых, температура газа должна быть не слишком низкой и не слишком высокой, чтобы абсолютное значение потенциальной энергии межмолекулярного взаимодействия было пренебрежимо мало́ по сравнению с кинетической энергией теплового движения молекул.

Получим ещё одно уравнение, связывающее все три макропараметра. Для этого вернёмся к формуле, в которой мы уже расписали концентрацию газа через отношение числа его молекул к занимаемому объёму:

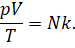
Давайте выразим число молекул газа через постоянную Авога́дро, массу и молярную массу газа из формул для количества вещества:

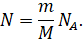
И подставим это значение в исходную формулу: .

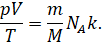
Произведение двух постоянных (Больцмана и числа Авогадро) называют универсальной (или молярной) газовой постоянной. О её физическом смысле этой постоянной мы с вами будем говорить немного позднее.

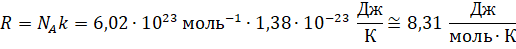
Тогда с учётом введённого обозначения можно записать, что произведение давления идеального газа и его объёма равно произведению отношения массы газа к его молярной массе, универсальной газовой постоянной и абсолютной температуры газа:

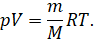
Это уравнение впервые было получено выдающимся русским учёным Дмитрием Ивановичем Менделеевым в 1874 году. Оно тоже является уравнением состояния идеального газа, и поэтому его называют уравнением Клайперона — Менделеева.

Из него вытекают два очень важных следствия. Во-первых, если выразить из уравнения число молекул газа, то можно заметить, что если различные газы занимают равные объёмы при одинаковых температурах и давлениях, то число молекул в них тоже одинаково. Иными словами, из него вытекает установленный опытным путём закон Авогадро, о котором мы упоминали на прошлых уроках: при равных давлениях и температурах в одинаковых объёмах любых газов содержится одинаковое число молекул.

А второе следствие мы рассмотрим на таком примере. Пусть у нас есть смесь химически не реагирующих разрежённых газов, находящихся в сосуде вместимостью V. Тепловое движение частиц каждого газа равномерно распределяет их по всему объёму сосуда. В результате столкновений частиц друг с другом в смеси устанавливается тепловое равновесие.

Общее число частиц газов в сосуде равно сумме частиц каждого из газов:

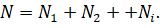
Конечно же, каждый газ в отдельности будет создавать давление на стенки сосуда. Оно называется парциальным давлением. То есть парциальное давление — это давление газа, входящего в состав газовой смеси, если бы он один занимал весь объём, предоставленный смеси, при той же температуре.

Запишем для каждого газа уравнение состояния:

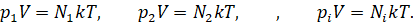
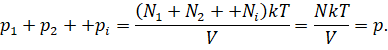
Можно записать, что давление смеси химически не реагирующих между собой газов равно сумме парциальных давлений каждого из газов.

Этот закон называют законом Дальтона, так как открыт он был экспериментальным путём в 1801 году английским учёным Джоном Дальтоном.

Для закрепления нового материала решим с вами задачу. Баллон вместимостью 20 л, содержащий газ при давлении 3 МПа и температуре 320 К, соединили с пустым баллоном вместимостью 5,0 л. Определите давление газа, которое установилось в баллонах после расширения, если температура газа стала равной 285 К.

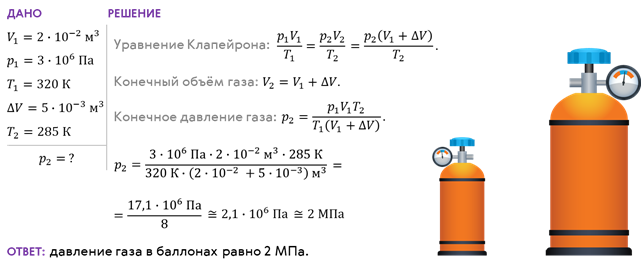
В заключение отметим, что уравнение Клайперона — Менделеева справедливо для любой массы газа и связывает между собой параметры одного состояния газа. Использование этого уравнения позволяет описать различные процессы, происходящие в идеальном газе.