– Паша, привет. Хочешь мандарин?
– Привет, Саша. Да, хочу. Я очень люблю мандарины.
– Смотри, у меня 3 мандарина, нас двое. Надо как-то эти мандарины разделить.
– Давай почистим все мандарины, посчитаем, сколько всего долек, и поделим их на 2.
– Давай. Смотри, в каждом мандарине 12 долек. У нас 3 мандарина, значит, и долек 36. Каждому получается по 18 долек.

– Подожди, Саша. Но мы можем же мандарины поделить и по-другому. Взять каждый по одному, а третий мандарин разделить пополам. В нём 12 долек, значит, каждый получит по 1 целому мандарину и по 6 долек.
– Ты прав, Паша. И как тогда записать? Если
мы берём по 18 долек, то можем это записать как 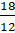 . Потому что в каждом мандарине по 12 долек. А если делим так, как ты
предложил, то записать как?
. Потому что в каждом мандарине по 12 долек. А если делим так, как ты
предложил, то записать как? 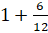 , что ли?
, что ли?
– Ничего не понимаю. Давай пойдём к Электроше. Он точно нам поможет разобраться.
– Электроша,
привет. Смотри, мы попробовали разделить на двоих 3 мандарина и у нас что-то не
очень понятное получилось. Если сначала мандарины разделить на дольки и делить
их, то получится, что каждый из нас должен взять 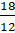 мандарина, а если сначала каждому взять по одному
целому мандарину, а оставшийся поделить на дольки, то получится, что у каждого
из нас 1 целый мандарин и ещё 6 двенадцатых мандарина. Как записать такое
деление?
мандарина, а если сначала каждому взять по одному
целому мандарину, а оставшийся поделить на дольки, то получится, что у каждого
из нас 1 целый мандарин и ещё 6 двенадцатых мандарина. Как записать такое
деление?

– Успокойтесь, ребята. Сейчас мы с вами во всём разберёмся, но сначала давайте устно выполним несколько упражнений.

Вернёмся к вашей задаче.
Запишем дробь 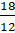 . Какая это дробь? Паша, ты помнишь, как называются такие дроби?
. Какая это дробь? Паша, ты помнишь, как называются такие дроби?
– Конечно, Электроша, помню. Числитель этой дроби больше знаменателя, значит, перед нами неправильная дробь.
Давайте подумаем, суммой каких дробей её можно представить?
– Ну, например, 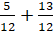 .
.
– Или 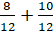 .
.
Мы можем ещё долго перечислять.

– Да, мальчики, вы правильные суммы
называете. А давайте запишем 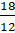 в виде суммы дробей
в виде суммы дробей 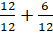 . Что вы можете сказать о дроби
. Что вы можете сказать о дроби 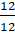 ?
?
– Числитель равен знаменателю, значит, эта
дробь равна 1. То есть нашу дробь можно записать так: 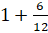 .
.
– А 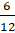 – это какая дробь?
– это какая дробь?
– Числитель меньше знаменателя, значит, это правильная дробь.

– Ой, – удивился Саша, – так у нас же получилось то же самое, когда мы сначала взяли себе по целому мандарину, а потом оставшийся мандарин поделили пополам.
– Конечно, Саша. У вас и должно было так получиться.
У нас получилось, что неправильную дробь мы представили в виде суммы натурального числа и правильной дроби.

Давайте посмотрим, может, это только дробь 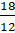 можно так представить?
можно так представить?
Возьмём дробь 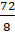 . И представим её в виде суммы двух дробей
. И представим её в виде суммы двух дробей 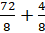 .
.
Чему равна дробь 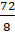 ? Паша, ты можешь подсчитать?
? Паша, ты можешь подсчитать?
– Конечно. Эта дробь равна 9. Тогда получим,
что дробь 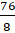 равна сумме
равна сумме 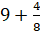 .
.

Опять получилась сумма натурального числа и правильной дроби. Так что получается, Электроша? Любую неправильную дробь можно представить в виде такой суммы?
– Да, запомните правило: любую неправильную дробь, у которой числитель не делится нацело на знаменатель, можно представить в виде суммы натурального числа и правильной дроби.
Обратите внимание на слова «числитель не
делится нацело на знаменатель». Если же числитель делится нацело на
знаменатель, например, дробь  , то такая дробь равна просто натуральному числу, в нашем случае, 3.
, то такая дробь равна просто натуральному числу, в нашем случае, 3.

Но вернёмся к нашим примерам. Как правило, такие суммы записывают так 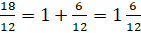 ,
, 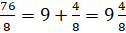 и читают: «одна целая шесть
двенадцатых» и «девять целых четыре восьмых».
и читают: «одна целая шесть
двенадцатых» и «девять целых четыре восьмых».
Числа такого вида называют смешанными числами. Ну, почему такое название, я думаю, вам понятно.

– Да, Электроша, ясно. Смешали натуральные числа и дробные, вот и получились смешанные числа.
– Да, Саша, ты прав. У каждого компонента смешанной дроби есть своё название.
Так, натуральное число называют целой частью смешанного числа, а дробь – дробной частью смешанного числа.
Обратите внимание, дробная часть смешанного числа – это обязательно правильная дробь.

Например, число 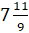 – это несмешанное число, потому что
– это несмешанное число, потому что 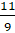 – это неправильная дробь.
– это неправильная дробь.

– Всё понятно, Электроша. А дай нам задание, чтобы проверить, как мы поняли, что такое смешанные числа.
– Хорошо.
Среди предложенных чисел 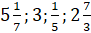 укажите смешанные. Начинай ты, Паша.
укажите смешанные. Начинай ты, Паша.
– 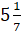 – это смешанное число. У него есть целая часть и дробная
часть. В дробной части – правильная дробь.
– это смешанное число. У него есть целая часть и дробная
часть. В дробной части – правильная дробь.
Число 3 несмешанное, так как у него нет дробной части.
 тоже несмешанное число, потому что у него нет целой
части.
тоже несмешанное число, потому что у него нет целой
части.
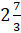 – это несмешанное число, потому что в дробной части
этого числа находится неправильная дробь.
– это несмешанное число, потому что в дробной части
этого числа находится неправильная дробь.
– Молодец, Паша.

Сейчас мы с вами научимся переводить неправильную дробь в смешанное число.
То есть разберём то, как правильно выделять или, другими словами, находить целую и дробную части числа.
Давайте посмотрим на дробь 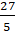 . Это неправильная дробь, и 27 без остатка на 5 не делится. То есть мы
точно можем представить эту дробь суммой натурального числа и правильной дроби,
другими словами, смешанным числом.
. Это неправильная дробь, и 27 без остатка на 5 не делится. То есть мы
точно можем представить эту дробь суммой натурального числа и правильной дроби,
другими словами, смешанным числом.
Выполним деление с остатком числа 27 на 5.
Получим, что 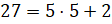 . Здесь 5 – это неполное частное, а 2 – остаток. Тогда целой частью
смешанного числа будет число 5, а числителем дробной части – число 2.
Знаменателем дробной части смешанного числа будет знаменатель неправильной
дроби, то есть 5.
. Здесь 5 – это неполное частное, а 2 – остаток. Тогда целой частью
смешанного числа будет число 5, а числителем дробной части – число 2.
Знаменателем дробной части смешанного числа будет знаменатель неправильной
дроби, то есть 5.

– Ну как, мальчики, вы всё поняли?
– Вроде бы, да. Но давай решим какое-нибудь задание, чтобы нам стало ещё яснее.
– Хорошо.
Вот задание для тебя, Саша.
Переведите неправильные дроби в смешанные числа 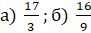 .
.
Первая дробь – 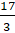 . Разделим 17 на 3. Получим, что
. Разделим 17 на 3. Получим, что 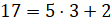 . Тогда можем записать, что
. Тогда можем записать, что 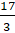 равно смешанному числу
равно смешанному числу 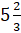 .
.
– Я так понял, Электроша?
– Да, Саша. Ты всё правильно понял. Продолжай.
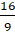 . Разделим 16 на 9 с остатком. Получим, что
. Разделим 16 на 9 с остатком. Получим, что 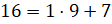 . Тогда дробь
. Тогда дробь 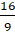 равна
равна 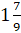 .
.
– Молодец, Саша.

Запомните правило: для того, чтобы неправильную дробь, у которой числитель не делится нацело на знаменатель, преобразовать в смешанное число, надо числитель разделить на знаменатель.
Полученное неполное частное записывается как целая часть смешанного числа, а остаток – как числитель дробной части смешанного числа.
Знаменатель дробной части будет равен знаменателю неправильной дроби.

Теперь давайте вернёмся к предыдущему правилу и немного его исправим. Теперь можно записать так: любую неправильную дробь, у которой числитель нацело не делится на знаменатель, можно представить в виде смешанного числа.
Ну что, вам стало понятно, что такое смешанные числа и как неправильные дроби в них переводить?
– Да, это понятно. Но вот интересно, а смешанное число можно перевести в неправильную дробь?
– Да, Паша. Можно.
Давайте возьмём, например, число
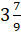 .
.
Представим это число в виде суммы 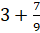 .
.
Мы помним, что любое натуральное число можно
представить в виде дроби с любым знаменателем. Представим 3 в виде дроби со
знаменателем 9. Получим, что смешанное число равно 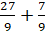 . Как складываются дроби с одинаковыми знаменателями, мы знаем
. Как складываются дроби с одинаковыми знаменателями, мы знаем 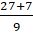 . Получим, что
. Получим, что 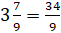 .
.

Попробуй, Саша, перевести число
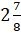 в неправильную дробь.
в неправильную дробь.
– Представим это число в виде суммы 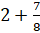 . 2 запишем как
. 2 запишем как 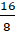 . Сложим
. Сложим 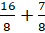 и получим, что
и получим, что 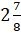 можно представить в виде неправильной дроби
можно представить в виде неправильной дроби 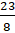 .
.
Есть правило, которое помогает упростить перевод смешанного числа в неправильную дробь.
Для того, чтобы преобразовать смешанное число в неправильную дробь, надо целую часть числа умножить на знаменатель дробной части. К полученному произведению надо добавить числитель дробной части. Эту сумму записать как числитель неправильной дроби, а в её знаменатель записать знаменатель дробной части смешанного числа.

Вернёмся к нашим примерам и попробуем перевести смешанное число в дробь
по этому правилу 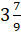 ,
, 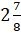 .
.
Начнём с 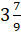 . Умножим 3 на 9 и прибавим 7. Это будет числитель неправильной дроби, а
знаменателем дроби будет число 9. Получим дробь
. Умножим 3 на 9 и прибавим 7. Это будет числитель неправильной дроби, а
знаменателем дроби будет число 9. Получим дробь 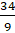 .
.
Попробуй, Паша, перевести этим способом в дробь число 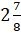 .
.
– Умножим 2 на 8 и добавим 7. Получим, что
числитель неправильной дроби будет равен 23. А знаменатель – 8. 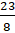 .
.
– Молодец, Паша.
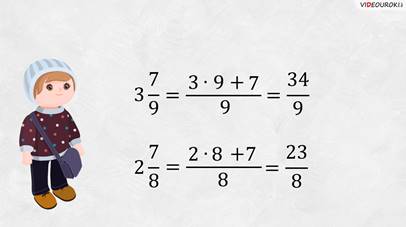
Выполните такое задание.
Преобразуйте смешанные числа в дроби, а
неправильные дроби – в смешанные числа 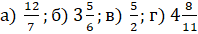 .
.
Начинай ты, Саша.
– Итак, дробь 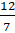 .
.
Разделим 12 на 7 с остатком. Получим 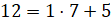 . Тогда
. Тогда 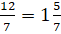 .
.
Переведём
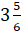 в неправильную дробь. Умножим 3 на 6 и добавим 5. Получим,
что числитель дроби равен 23. Знаменатель дроби будет равен 6.
в неправильную дробь. Умножим 3 на 6 и добавим 5. Получим,
что числитель дроби равен 23. Знаменатель дроби будет равен 6.
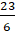 .
.
– Теперь, Паша, продолжи решать ты.
Дробь  . Разделим 5 на 2 с остатком. Получим
. Разделим 5 на 2 с остатком. Получим 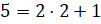 . То есть дробь
. То есть дробь 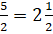 .
.
Для того, чтобы перевести число
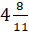 в неправильную дробь, умножим 4 на 11 и прибавим 8.
Числитель дроби будет равен 52. Знаменатель дроби будет равен 11.
в неправильную дробь, умножим 4 на 11 и прибавим 8.
Числитель дроби будет равен 52. Знаменатель дроби будет равен 11.


 Получите свидетельство
Получите свидетельство Вход
Вход



 0
0 8664
8664