Опыты с зеркалами, которые мы проводили на прошлом занятии, позволили нам прикоснуться к удивительному миру симметрии.
В переводе с греческого слово «симметрия» означает «соразмерность, пропорциональность, одинаковость в расположении частей».
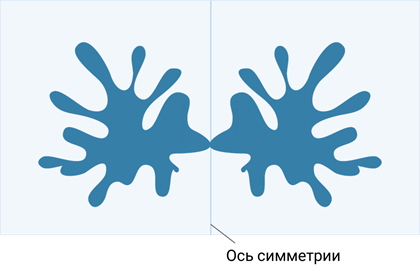
Посмотрите на кленовый лист, бабочку, снежинку. Их объединяет то, что они симметричны. Если мы на каждом из рисунков начертим прямую вот таким образом…

А затем поставим зеркальце вдоль этой прямой на каждом рисунке, то отражённая в зеркале половинка фигуры дополнит её до целой (такой же, как исходная фигура).

Поэтому такая симметрия называется зеркальной (или осевой, если речь идёт о плоскости). Прямая, вдоль которой поставлено зеркало, называется осью симметрии.
Если симметричную фигуру сложить пополам вдоль оси симметрии, то её части совпадут.
С симметрией мы постоянно встречаемся в повседневной жизни. Люди используют симметрию в орнаментах, предметах быта, технике. Издавна человек использовал симметрию в архитектуре. Древним храмам, башням средневековых замков, современным зданиям она придаёт гармоничность, законченность. Симметрия также встречается в природе. Она создаёт ощущение порядка, гармонии, красоты.
Давайте сделаем кляксу. Для этого на лист бумаги капнем чернил. Сложим лист вдвое, а затем разогнём. Линия сгиба листа является осью симметрии кляксы.
Получается, что клякса имеет одну (вертикальную) ось симметрии.
А вот у снежинки 6 линий сгиба и все они являются осями симметрии.

У геометрических фигур может быть одна или несколько осей симметрии, а может и не быть совсем.
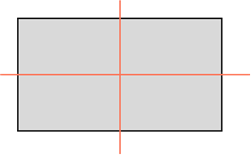
Так, прямоугольник обладает двумя осями симметрии, каждая из которых проходит через середины двух его противоположных сторон. То есть, вырезав прямоугольник из бумаги и перегнув его по любой из двух осей симметрии, половинки фигуры совпадут.
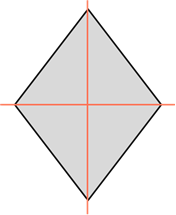
Ромб также обладает двумя осями симметрии. Это прямые, которые содержат его диагонали.
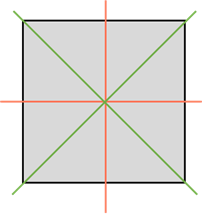
Квадрат имеет четыре оси симметрии. Две проходят через середины его противоположных сторон. И ещё две – это прямые, которые содержат его диагонали.
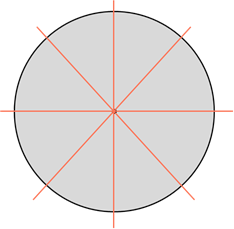
Круг. Его осью симметрии является любая прямая, которая проходит через его центр, то есть содержит диаметр круга. А значит, круг имеет бесконечно много осей симметрии
Теперь посмотрите на следующую фигуру. Это произвольный параллелограмм. У него нет ни одной оси симметрии.

У произвольного треугольника тоже нет осей симметрии.
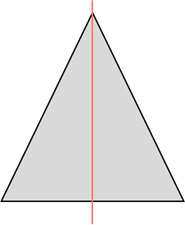
У равнобедренного треугольника есть одна ось симметрии.
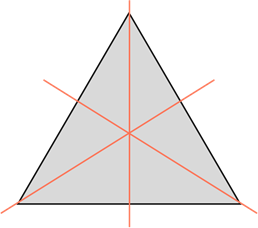
У равностороннего (то есть у правильного) треугольника – три оси симметрии.
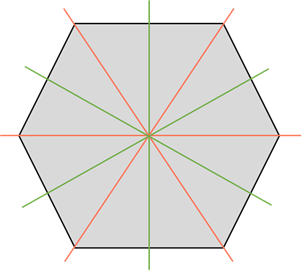
Теперь посмотрите на шестиугольник. У него три оси симметрии, которые проходят через противоположные вершины, и ещё три оси, которые проходят через середины противоположных сторон. То есть всего шесть осей симметрии.
Таким образом, мы можем сказать, что круг – «самая симметричная» фигура из рассмотренных, так как он имеет бесконечно много осей симметрии.
Сейчас давайте посмотрим на следующие фигуры и выясним, какая из них лишняя.
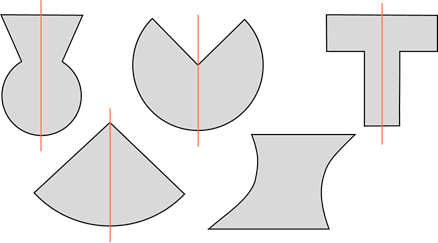
Итак, первая фигура напоминает замочную скважину. Она имеет одну ось симметрии.
Вторая фигура тоже имеет одну ось симметрии.
У третьей фигуры (в виде буквы Т) одна ось симметрии.
У четвёртой тоже одна. А вот пятая фигура не имеет ни одной оси симметрии. И поэтому она лишняя.
Теперь давайте посмотрим на следующие пять фигур. Что у них общего?
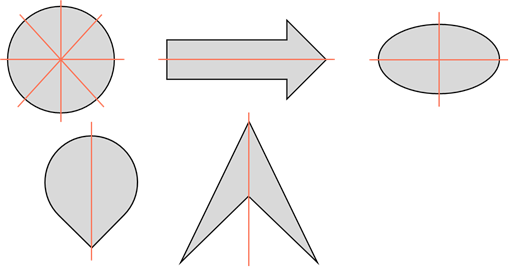
Первая фигура – круг. Выше мы выяснили, что у круга бесконечно много осей симметрии. Вторая фигура (в виде стрелки) имеет только одну ось симметрии. Третья фигура – эллипс. У эллипса две оси симметрии. Четвёртая фигура имеет одну ось симметрии. Пятая фигура тоже имеет одну ось симметрии. Каждая фигура имеет хотя бы одну ось симметрии.
На предыдущем занятии мы с вами проводили опыт с двумя плоскими зеркалами. С помощью составленного из двух зеркал калейдоскопа мы получали симметричные фигуры.
Давайте изобразим в виде прямых два зеркала под углом 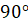 друг к
другу. Затем нарисуем в одном из углов некоторую линию и, не пользуясь
настоящими зеркалами, дорисуем её до симметричной фигуры, которая получилась бы
при отражении в зеркалах. Полученная фигура имеет две оси симметрии. Понятно,
что угол ними равен
друг к
другу. Затем нарисуем в одном из углов некоторую линию и, не пользуясь
настоящими зеркалами, дорисуем её до симметричной фигуры, которая получилась бы
при отражении в зеркалах. Полученная фигура имеет две оси симметрии. Понятно,
что угол ними равен 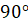 .
.
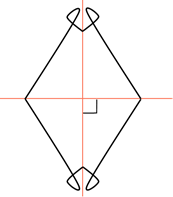
Посмотрите на рассмотренные выше фигуры, которые имеют две оси
симметрии. Угол между осями равен 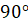 .
.
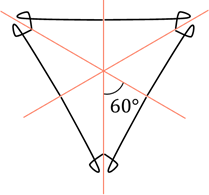
Если, например, мы поставим зеркала под углом 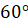 друг к
другу, то линия отразится 5 раз, а полученная фигура будет иметь 3 оси
симметрии.
друг к
другу, то линия отразится 5 раз, а полученная фигура будет иметь 3 оси
симметрии.
Давайте научимся точно строить отражение фигуры в зеркале.
Представим, что прямая l – зеркало (или ось симметрии). Изобразим некоторую ломаную 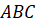 и построим
её отражение в зеркале.
и построим
её отражение в зеркале.
Итак, из вершин  ,
, 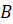 и
и 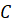 опускаем перпендикуляры на прямую l. Затем продолжаем их «за
зеркало» на такое же расстояние (равное длине соответствующего отрезка).
Получаем точки
опускаем перпендикуляры на прямую l. Затем продолжаем их «за
зеркало» на такое же расстояние (равное длине соответствующего отрезка).
Получаем точки  ,
, 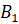 и
и 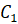 . Соединяем
эти точки. Ломаная
. Соединяем
эти точки. Ломаная 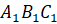 является
отражение ломаной
является
отражение ломаной 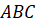 .
.
Можно сказать, что ломаная 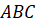 симметрична
ломаной
симметрична
ломаной 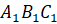 относительно
прямой l.
относительно
прямой l.
Построим с вами треугольник, симметричный треугольнику 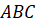 относительно
прямой l.
относительно
прямой l.
Из вершин  и
и 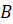 опустим
перпендикуляры на прямую l. Затем продолжим их за прямую l на такое же расстояние
(равное длине соответствующего отрезка). Получим точки
опустим
перпендикуляры на прямую l. Затем продолжим их за прямую l на такое же расстояние
(равное длине соответствующего отрезка). Получим точки  и
и 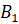 .
.
При этом точка 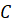 осталась на
месте. Она лежит на оси симметрии. Она симметрична сама себе.
осталась на
месте. Она лежит на оси симметрии. Она симметрична сама себе. 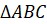 и
и 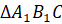 симметричны
относительно прямой l.
симметричны
относительно прямой l.
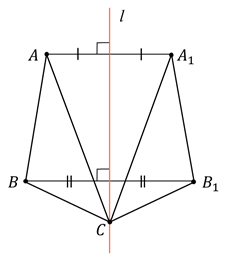
А сейчас посмотрите на рисунок.

Давайте выясним, симметрична ли точка  точке
точке  относительно
прямой l. Для этого мы соединим точки
относительно
прямой l. Для этого мы соединим точки  и
и  . Затем с
помощью угольника проверим, перпендикулярна ли прямая l отрезку
. Затем с
помощью угольника проверим, перпендикулярна ли прямая l отрезку 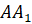 . Перпендикулярна.
. Перпендикулярна.
Потом с помощью линейки проверим, делит ли прямая l отрезок  и
и  пополам. Делит.
пополам. Делит.

Значит, точки  и
и  симметричны
относительно прямой l.
симметричны
относительно прямой l.
Кроме симметрии относительно прямой существует ещё симметрия
относительно точки, так называемая центральная симметрия. Она
характеризуется наличием центра симметрии – точки О, которая обладает
определённым свойством. Можно сказать, что точка О является центром
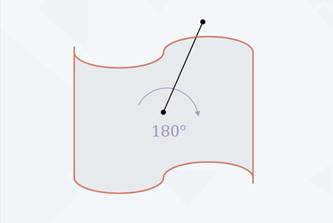
симметрии, если при повороте вокруг точки О на 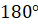 фигура
переходит сама в себя.
фигура
переходит сама в себя.
Понятие центральной симметрии распространяется и на трёхмерное пространство.
Проверить, является ли фигура центрально-симметричной или нет,
можно с помощью обычной иголки и кальки. Наложим на нашу фигуру кальку. Затем,
проколов фигуру в предполагаемом центре и обведя её контур, надо повернуть фигуру
на 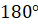 вокруг
иголки. Если фигура «вошла» в свой контур, то она центрально-симметричная.
вокруг
иголки. Если фигура «вошла» в свой контур, то она центрально-симметричная.
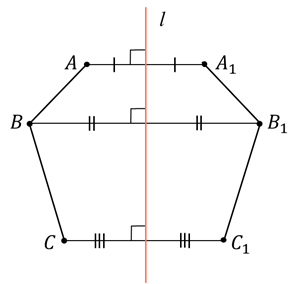
Сейчас посмотрите на плоские фигуры, которые имеют и центр симметрии, и оси симметрии.
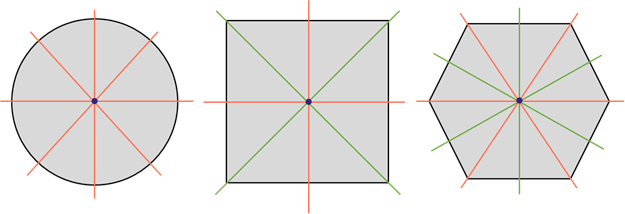
Это круг. Выше мы сказали, что он имеет бесконечно много осей симметрии, каждая из которых содержит его диаметр. А вот центром симметрии круга является его центр.
Квадрат имеет четыре оси симметрии. Центром симметрии квадрата является точка пересечения его диагоналей.
У шестиугольника шесть осей симметрии. Центром его симметрии является точка пересечения его диагоналей.
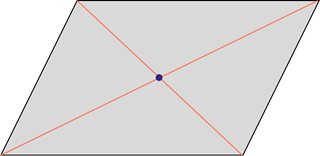
Выше мы сказали, что произвольный параллелограмм не имеет ни одной оси симметрии. Но он имеет центр симметрии – это точка пересечения его диагоналей.
А вот, например, равнобедренный треугольник имеет ось симметрии, но не имеет центра симметрии. То же самое можно сказать и про пятиугольник, у которого есть оси симметрии, но центра симметрии нет.

 Получите свидетельство
Получите свидетельство Вход
Вход




 12094
12094

