Решение задач на нахождение четвёртого пропорционального

Ох, привет, ребята!

Я, как всегда, в заботах и хлопотах. Дело в том, что в нашем саду в этом году был отличный урожай овощей и фруктов. Все это хранится в подвалах нашего замка. А сегодня царица Математика приказала отправить часть наших запасов в школу юных математиков. И вот теперь мне надо разложить эти фрукты и овощи по ящикам и пакетам. Но прежде, чем приступить к работе, я все точно рассчитаю.

А поможет мне в этом умение решать задачи на нахождение четвёртого пропорционального. И я предлагаю вам тоже присоединиться к решению таких задач.

Ой, я слышу, что некоторые ребята говорят, что они уже умеют решать такие задачи – мы, мол, уже их решали.

Такие, да не совсем такие. Так что, давайте скорее в них разбираться. Вот первая задача.

Тридцать два килограмма лука мы уже разложили в пакеты по четыре килограммов в каждый пакет. Сколько килограммов чеснока можно расфасовать в такое же количество меньших по размеру пакетов, если в каждый пакет входит два килограмма чеснока?

Как всегда, для решения задач на нахождение четвёртого пропорционального, нужно нарисовать таблицу. Вот таблица из трёх колонок.

И, конечно, в названии первой колонки будет число один. Масса содержимого ОДНОГО пакета. Во второй колонке, по традиции, есть слово количество – количество пакетов. Ну и третья колонка – масса содержимого ВСЕХ пакетов.

Что известно в задаче?

Тридцать два килограмма – это масса всех пакетов с луком. Ещё про лук мы знаем, что масса каждого пакета с луком – четыре килограмма. В нашей задаче есть ещё число два килограмма. Это масса одного пакета с чесноком. Надо узнать, массу всех пакетов с чесноком.

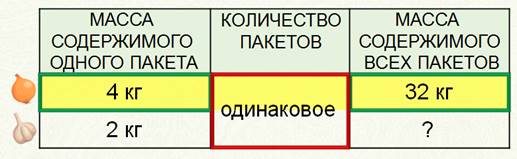
А что же написать в колонку Количество пакетов? Это неизвестно. Про них только сказано, что количество пакетов с чесноком такое же, как и количество пакетов с луком. Поэтому просто напишем, что количество пакетов одинаковое. Теперь внимательно смотрим на таблицу и находим строчку, в которой есть два данных. Имея два данных, мы можем найти третье. Нам известна масса всего лука и масса одного пакета с луком, а неизвестно количество пакетов. Как это можно найти? Вот как фасовался лук.

Мы весь лук разложили поровну, по четыре килограмма в пакеты, то есть, выполняли действие деления.

32 : 4 = 8 (п.)

Получилось восемь пакетов с луком.

По условию задачи мы знаем, что пакетов с чесноком столько же, сколько и с луком, и масса каждого пакета чеснока – два килограмма. Теперь мы можем узнать, сколько всего чеснока. По два килограмма восемь пакетов, то есть, восемь раз, получается шестнадцать килограммов чеснока.

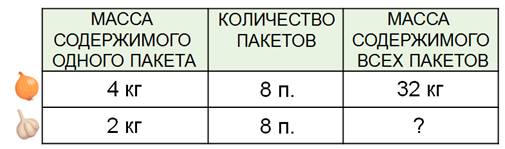
2 × 8 = 16 (кг)

Ответ: 16 кг чеснока.

Ну вот, задачка и решена. Отправим малышам шестнадцать килограммов чеснока и тридцать два килограмма лука.

А теперь возьмёмся за яблоки и груши. Их мы будем складывать в ящики.

В кладовой стоит двадцать одинаковых ящиков с яблоками, в которых разложено восемьдесят килограммов яблок. Сколько таких же ящиков необходимо принести, чтобы разложить ещё сорок килограммов груш?

Опять, прежде чем приступить к решению задачи, составим краткое условие в виде таблицы.

Первая колонка – масса содержимого ОДНОГО ящика, вторая – количество ящиков, третья – масса содержимого ВСЕХ ящиков.

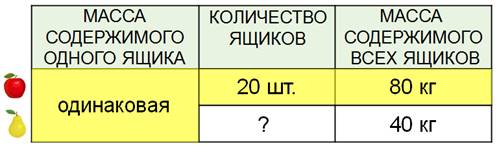
Двадцать ящиков – количество, восемьдесят килограммов – масса всех яблок. Сорок килограммов – масса всех груш, которые осталось разложить по ящикам. Ну, а раз ящики такие же, то масса яблок и груш в них будет одинаковой.

В первой строке таблицы есть два данных – масса всех яблок и количество ящиков. Имея два данных, можно найти третье – массу содержимого одного ящика. Когда яблоки раскладывали поровну по ящикам, выполняли действие деления. Вот и мы разделим массу всех яблок на количество ящиков.

1) 80 : 20 = 4 (кг) – масса яблок в одном ящике

Ящики с грушами будут такие же по своей массе, поэтому во второй строчке таблицы у нас стало известно ещё одно данное – четыре килограмма – масса содержимого одного ящика. Так, два данных у нас есть. Находим третье – количество ящиков, необходимое для того, чтобы разложить груши. Мысленно раскладываем груши по ящикам – сорок килограммов по четыре килограмма.

Это тоже действие деления.

40 : 4 = 10 (ящ.)

Ответ: 10 ящиков.

Десять ящиков необходимо для того, чтобы разложить все груши. Ну вот, все расчёты выполнены, можно приступать к работе. Хотя… Нет, не могу не поделиться. Я ведь заметил, что решить эту задачу можно и другим способом.

Посмотрите ещё раз внимательно на таблицу.

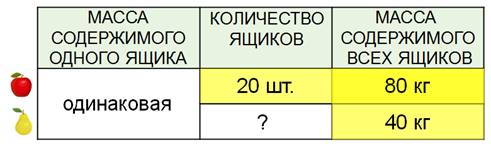
Мы с вами перед тем, как приступить к решению, выбирали строчку, в которой есть два данных. А что если выбирать не строчку, а столбик? В нашей таблице два известных данных есть в третьем столбике. Там указано, что яблок – восемьдесят килограммов, а груш – сорок. С такими числами мы можем узнать, во сколько раз груш меньше, чем яблок. Восемьдесят делим на сорок, получается – в два раза меньше.

80 : 40 = 2 (раза) – меньше

А если груш в два раза меньше, значит, и ящиков для них нужно в два раза меньше. Поэтому можно двадцать разделить на два.

20 : 2 = 10 (ящ.)

Ответ: 10 ящиков.

Видите, ответ такой же, как и в первом способе – десять ящиков. Значит, задачу можно было решить и таким способом. Правда, не каждую задачу на нахождение четвёртого пропорционального можно решать двумя способами. Эту задачу мы смогли решить таким способом потому, что в паре чисел, находящихся в одном столбике, одно из них можно было разделить на другое, то есть это кратные числа. Бывают такие задачи, которые можно решить только первым способом, выбирая в таблице строчку с двумя данными. Но встречаются и такие, которые можно решить только вторым способом, выбирая в таблице столбик с двумя данными, кратными друг другу. Будьте внимательны при выборе способа решения задачи.

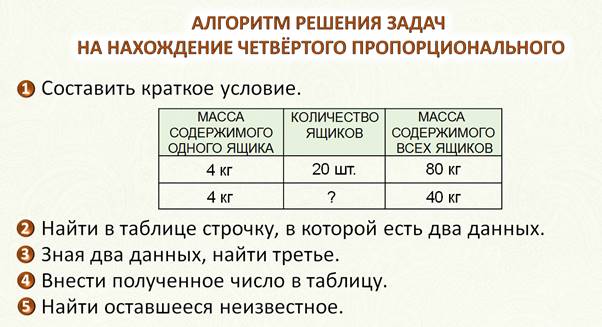
Ну, что, время не ждёт. Пора делами заниматься. Но, прежде чем расстаться, я хочу ещё раз вам напомнить. Для решения задач на нахождение четвёртого пропорционального нужно:

* Составить краткое условие в виде таблицы из трёх колонок, в первой из которых, обычно, встречается слово «один» – масса содержимого одного пакета, или одного ящика. Вторая колонка – количество – ящиков, пакетов. Третья колонка – масса содержимого всех пакетов, ящиков.

* Найти в таблице строчку, в которой есть два данных.

* Зная два данных, найти третье.

* Внести полученное число в таблицу. При этом и в другой строке таблицы становится известным два числа.

* Найти оставшееся неизвестное.

Но иногда задачу можно решить и другим способом, так как я сегодня вам показал – сравнивать числа не в строчках, а в колонках.

Ну все, поспешу я продукты разложить и отправить. А с вами я сегодня прощаюсь. Всего вам хорошего!