Моделирование корреляционных зависимостей

Прежде чем приступить к изучению новой темы, давайте повторим некоторые важные моменты из прошлых уроков.

Итак, в течение последних нескольких уроков мы с вами изучаем «Информационное моделирование». Как вы помните, в информационной модели отражаются знания человека об объекте моделирования. А информационная модель – это описание в той или иной форме объекта моделирования.

Математические модели также относятся к информационным моделям. Математической моделью называется совокупность математических соотношений, уравнений, неравенств, описывающих основные закономерности изучаемого объекта, процесса или явления.

Статистика — это род практической деятельности людей цель, которой сбор, обработка и анализ информации.

Также на прошлых уроках мы научились строить математическую модель по статистическим данным, а затем делать прогноз по полученной модели методом вычислений.

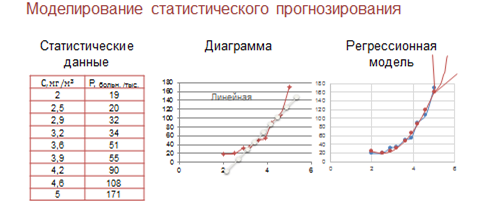
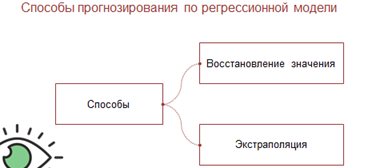
Есть два способа прогнозирования по регрессионной модели.

Первый способ. Если прогноз рассчитывается в пределах экспериментальных значений независимой переменной. Такой прогноз называется восстановлением значения.

Второй способ. Если прогноз рассчитывается за пределами экспериментальных данных. Такой прогноз называется экстраполяцией.

То есть на прошлых уроках, при построении регрессионной математической модели, мы с вами точно знали, что зависимость между двумя факторами существует.

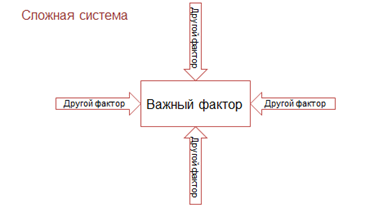
А что делать, если нужно рассмотреть и построить модель по сложно системе? В которой на один важный фактор влияют многие другие факторы?

Сегодня на уроке мы с вами будем разбираться со следующими вопросами:

·       Что такое корреляционная зависимость?

·       Какие возможности даёт корреляционный анализ?

·       А также разберёмся, какие задачи можно решать с помощью корреляционного анализа.

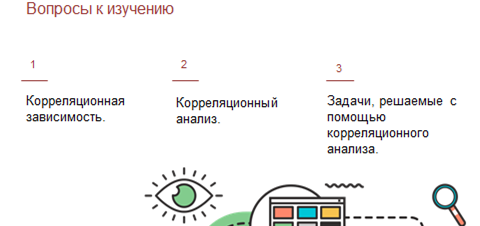
Важнейшей целью статистики является изучение объективно существующих связей между явлениями. Например, на прошлом уроке мы рассматривали связь между содержанием угарного газа в воздухе и числом заболевших людей астмой.

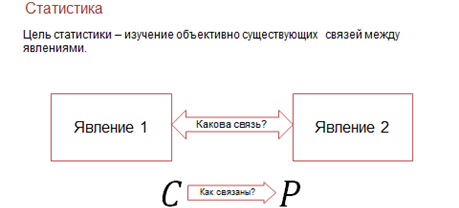
В ходе статистического исследования связей между явлениями, необходимо показать причинно-следственные зависимости между показателями, т.е. насколько изменение одних показателей зависит от изменения других показателей. В нашем примере как влияет увеличение содержания угарного газа в воздухе на число больных астмой.

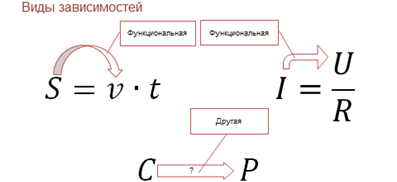
Существует два вида зависимостей. Вам уже хорошо знакомая — функциональная (если определённому значению переменной «x» соответствует строго определённое значение «y»).

Помните, мы рассматривали зависимость пути от времени.

Однако далеко не всегда зависимость может быть простой (или относительно простой). Часто случается так, что данному значению одной величины соответствует целый ряд значений другой, причём при изменении данной величины меняются и другие значения, а также и его среднее.

В таких случаях говорят о корреляционной зависимости.

Корреляционная зависимость – это зависимость между величинами, каждая из которых подвергается неконтролируемому разбросу.

Образцовым примером такой зависимости является связь между ростом отцов и детей. Конечно, у высокого отца может быть низкорослый сын, а у низкорослого — высокий, но в большинстве случаев прослеживается склонность увеличения роста детей с увеличением роста отцов.

Также примерами корреляционных зависимостей являются: зависимость между количеством удобрений и урожайностью, спросом на товары и ценой на рынке. Зависимость стажа работы на производительность труда рабочего.

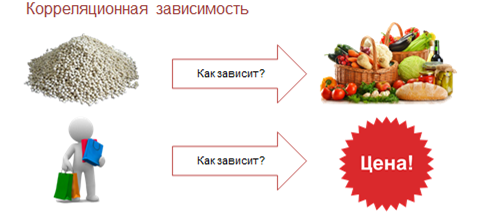
Естественно, стаж влияет на производительность, но он не может определять её полностью, так как на производительность также влияют квалификация и образование рабочего, возраст и его состояние здоровья, да и другие факторы.

То есть можно сделать вывод, что стаж далеко не единственный фактор производительности. И связь между этими переменными – корреляционная.

Раздел математической статистики, который исследует корреляционные зависимости, называется корреляционным анализом.

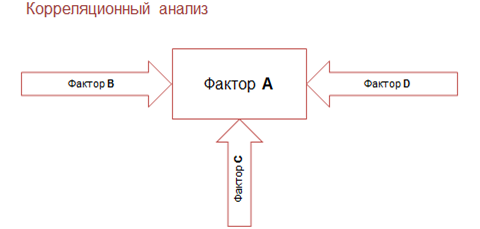
Пусть важным свойством какой-то сложной системы является фактор А.

На А могут оказывать влияние многие другие факторы, например, B, C и D.

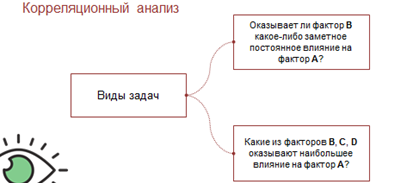
При изучении корреляционных зависимостей мы рассмотрим два вида задач.

Первый вид – Оказывает ли фактор В какое-либо заметное постоянное влияние на фактор А?

И второй – Какие из факторов B, C или D оказывают наибольшее влияние на фактор А?

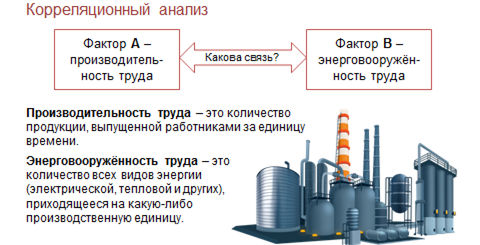
Рассмотрим пример сложной системы на предприятии: здесь факторам А будет производительность труда рабочих, то есть количество продукции, выпущенной работниками за единицу времени.

Фактором B рассмотрим так называемую «Энерговооружённость труда», то есть количество всех видов энергии (электрической, тепловой и других), приходящееся на какую-либо производственную единицу.

Специалисты по статистике знают, что для того, чтобы выявить зависимость от какого-то определённого фактора, нужно максимально исключить влияние других факторов. Иначе говоря, мы будем рассматривать предприятия, которые занимаются выпуском подобной продукции, но с разной энерговооружённостью. То есть предприятие может быть прибыльным или убыточным. Иметь широкий рынок сбыта продукции, или узкий.

Будем рассматривать производительность труда в тысячах рублей и энерговооружённость в киловаттах, в расчёте на одного работающего, для 14 предприятий.

Напомним, статистические данные являются относительными или усреднёнными.

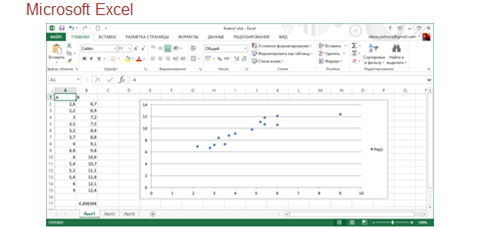
Итак, перед нами таблица сбора данных по 14 предприятиям. Построим по этим данным точечную диаграмму. Для этого выделяем диапазон ячеек А2 B 15. На вкладке Вставка в разделе Диаграммы выбираем тип диаграммы – точечная, вид – точечная с маркерами.

Обратите внимание, значения обеих величин: производительность труда и энерговооружённость – имеют существенный разброс. И кажется, что никакой взаимосвязи между ними нет, но она вполне может быть.

Мы получили графическое представление корреляционной зависимости.

Корреляционный анализ изучает вероятностную зависимость каждой из величин, при которой изменение одной величины ведёт к изменению распределения другой, а также меру такой зависимости.

Оценку корреляции величин начинают с высказывания гипотезы о возможном характере зависимости между их значениями.

Чаще всего считают, что это линейная зависимость. Тогда мера корреляционной зависимости – это величина, которая называется коэффициентом корреляции.

Коэффициент корреляции (обычно обозначают греческой буквой ƍ) характеризует величину отражающую степень взаимосвязи двух переменных между собой.

Он может изменяться в пределах от -1 до +1. (здесь и далее читать: единица)

Если ƍ равно нулю то, это говорит об отсутствии корреляционных связей между величинами. Причём, если ƍ близко к 1 (или -1) то говориться о сильной корреляции, а если близко к 0, то о слабой.

Если ƍ близко к + 1, то это означает что при увеличении (или уменьшении) значений одной переменной будет закономерное увеличение (или уменьшение) другой переменной т.е. взаимосвязи типа увеличение-увеличение (или уменьшение-уменьшение).

Если ƍ близко к - 1, то это означает, что при увеличении (или уменьшении) значений одной переменной будет закономерное уменьшение (или увеличение) другой переменной т.е. взаимосвязи типа увеличение-уменьшение (уменьшение-увеличение).

Для построения корреляционных зависимостей, а также для вычисления коэффициента корреляции ƍ удобно пользоваться табличным процессором Excel.

В Excel функция вычисления коэффициента корреляции называется CORREL и входит в группу статистических функций.

Давайте вычислим коэффициент корреляции для нашей зависимости.

Поместим курсор в любую свободную ячейку, например, B 17. Теперь на вкладке Формулы в разделе Библиотека функций нажимаем вставить функцию. В открывшемся окне мастера функций введём в окошко Поиск функции название функции CORREL и нажимаем поиск. Далее в окошке Выберите функцию нажимаем два раза мышкой по необходимой нам функции. В открывшемся окне функции CORREL в окошко Массив 1 укажем диапазон значений для фактора А, то есть А2 А15. В окошко Массив 2 укажем диапазон значений для фактора B, то есть B 2 B 15. И нажимаем Ок.

Теперь в ячейке Бэ 17 мы увидим ответ: ƍ равно ноль целых восемьсот девяносто восемь тысяч триста девяносто четыре миллионных (0, 898394)

Эта величина находится ближе к плюс единице, следовательно, можно сделать вывод, что корреляция сильная.

Наличие зависимости между производительность труда рабочих и энерговооружённостью нетрудно понять. Рабочие с удовольствием будут работать на предприятии, где сделан ремонт, обновлено и исправно рабочее оборудование, в помещениях хорошее освещение. На таких предприятиях люди работают легко и с удовольствием и, естественно, производительность их труда будет выше.

А сейчас давайте повторим главные моменты из сегодняшнего урока:

·       Корреляционная зависимость – это зависимость между величинами, каждая из которых подвергается неконтролируемому разбросу.

·       Раздел математической статистики, который исследует корреляционные зависимости, называется корреляционным анализом.

·       Коэффициент корреляции ƍ, характеризует величину отражающую степень взаимосвязи двух переменных между собой. Он может изменяться в пределах от -1 до +1.