Кроме призм для управления пучками света существуют и другие устройства, среди которых особое место занимают линзы.
Линза — это прозрачное тело, ограниченное криволинейными (чаще всего сферическими) или криволинейной и плоской поверхностями.
Слово линза с латинского переводится, как ‘чечевица’. Чечевица — это растение, плоды которого выглядят как короткие, приплюснутые с обеих сторон бобы.
Первое упоминание о линзах можно найти в древнегреческой пьесе Аристофа́на «Облака», датируемой 424 годом до нашей эры, где с помощью выпуклого стекла и солнечного света добывали огонь.
Из произведений Плиния Старшего следует, что такой способ разжигания огня был известен и в Римской империи. Там также описан, возможно, первый случай применения линз для коррекции зрения. Известно, что римский император Нерон смотрел гладиаторские бои через вогнутый изумруд для исправления близорукости.
Но самой древней считается линза Нимруда (или линза Лэйарда), созданная примерно в 750—710 годах до нашей эры и найденная при раскопках в городе Нимруд — одной из древних столиц Ассирии.

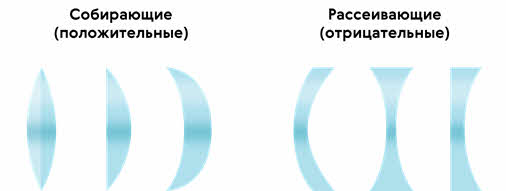
В зависимости от форм различают собирающие (положительные) и рассеивающие (отрицательные) линзы. К группе собирающих линз обычно относят линзы, у которых середина толще краёв (их ещё называют выпуклыми линзами), а к группе рассеивающих — линзы, края которых толще середины (вогнутые линзы).
Физической моделью реальной линзы служит тонкая линза. Так мы будем называть линзу, если её толщина мала по сравнению с радиусами сферических поверхностей линзы и расстоянием предмета от линзы.
Отметим сразу, что в дальнейшем, говоря о линзе, мы всегда будем иметь ввиду именно тонкую линзу.
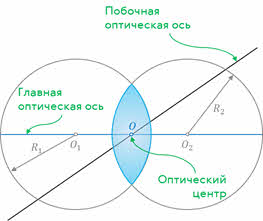
Для такой линзы вершины сферических поверхностей практически совпадают, и эту точку называют оптическим центром линзы.
Прямая, проходящая через центры сферических поверхностей, называется главной оптической осью линзы. Любая другая прямая, проходящая через оптический центр линзы, называют побочной оптической осью.
Теперь посмотрим, как с помощью линзы можно изменить направление падающих на неё лучей. Для этого поместим в центр оптической шайбы двояковыпуклую линзу и направим на неё луч света вдоль главной оптической оси.

Как видим, луч прошёл через линзу без преломления. Если направить луч света через оптический центр под некоторым углом к главной оптической оси, то он также не изменит своего первоначального направления. Следовательно, луч света проходит через оптический центр линзы без преломления.
Теперь направим на линзу пучок света, лучи которого параллельны главной оптической оси. Как видим, они пересеклись в одной точке, лежащей на главной оптической оси. Значит, двояковыпуклая линза собирает преломлённые лучи. Поэтому такая линза и называется собирающей.

Заменим линзу на двояковогнутую и повторим эксперимент. Не трудно заметить, что все лучи, кроме центрального, расходятся. Значит, двояковогнутая линза рассеивает параллельный пучок падающих на неё лучей. Поэтому такую линзу и принято называть рассеивающей.
Выпуклую линзу можно представить в виде совокупности плоскопараллельной пластинки (в середине) и усечённых призм, расширяющихся к середине призмы, а вогнутую — как совокупность плоскопараллельной пластинки и усечённых призм, расширяющихся к краям.
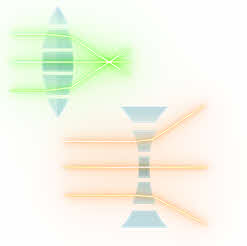
Напомним, что если призма сделана из оптически более плотного материала, чем окружающая среда, то она отклоняет луч к основанию. Именно поэтому параллельный пучок после преломления в выпуклой линзе станет сходящимся, а в вогнутой — расходящимся.
Точка, в которой пересекаются преломлённые линзой лучи, падающие параллельно главной оптической оси, или их продолжения, называется главным фокусом линзы. Обозначается он большой латинской буквой F.
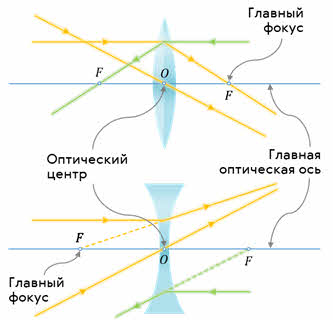
Главных фокусов у линзы два — передний и задний. Это обусловлено тем, что лучи света можно пустить как с одной, так и с другой стороны линзы. Оба фокуса лежат на главной оптической оси симметрично относительно оптического центра
Обратите внимание, что у собирающей линзы в фокусе пересекаются сами преломлённые лучи, а у рассеивающей линзы — их продолжения. Поэтому условились считать фокус собирающей линзы действительным, а рассеивающей — мнимым.
Расстояние от оптического центра линзы до её главного фокуса, называется фокусным расстоянием. Его тоже принято обозначать латинской буквой F, а единицей его измерения в СИ является метр:
[F] = [м].
Видоизменим наш опыт так, чтобы свет, идущий от источников, падал под некоторым углом к главной оптической оси. Как видим, пересечение лучей произошло не в главном фокусе, а в другой точке.
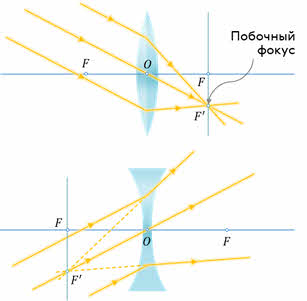
Причём эта точка находится в плоскости, проходящей через главный фокус перпендикулярно главной оптической оси. Она называется фокальной плоскостью, а точка, в отличие от главного фокуса, называется побочным фокусом или просто — фокусом.
Аналогично определяется фокальная плоскость и побочный фокус для рассеивающей линзы
Очевидно, что различные линзы будут по-разному преломлять лучи света. Например, более выпуклая линза преломляет лучи сильнее, чем более вытянутая, так как у последней больше фокусное расстояние. Чтобы количественно оценить преломляющую способность линзы, вводят величину, называемую оптической силой линзы, которая обратно пропорциональна фокусному расстоянию:
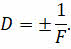
В записанной формуле знак «+» берётся для собирающей линзы, а «–» — для рассеивающей, так как её фокус мнимый.
Единицей измерения оптической силы в СИ служит м–1. Внесистемной же единицей измерения является диоптрия, которая, например в Российской Федерации, допускается к применению без ограничения срока наравне с единицами СИ с областью применения «оптика».
Очевидно, что оптическая сила равна одному диоптрию, если фокусное расстояние линзы равно одному метру:
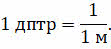
Опыт показывает, что общая оптическая сила двух или более линз, сложенных вместе, равна алгебраической сумме оптических сил этих линз:
D = D1 + D2 +… .
Основные свойства тонкой линзы главным образом определяются расположением её фокусов. Это означает, что, зная расстояние от источника света до линзы и её фокусное расстояние, можно без проблем найти расстояние до изображения, не рассматривая ход лучей внутри линзы. Следовательно, нет необходимости изображать на чертеже точный вид сферических поверхностей линзы. Поэтому собирающую и рассеивающую линзы обозначают символами, представленными на экране.
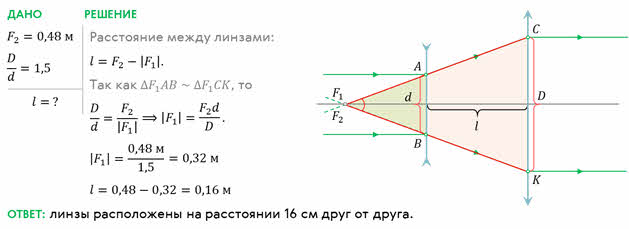
Для закрепления нового материала, решим с вами такую задачу. Главные оптические оси собирающей (фокусное расстояние 48 см) и рассеивающей линз совпадают. Цилиндрический пучок лучей, параллельный главным оптическим осям, падает на рассеивающую линзу. Пройдя через обе линзы пучок света остался параллельным. Если на выходе его диаметр увеличился в полтора раза, то на каком расстоянии друг от друга расположены линзы?

 Получите свидетельство
Получите свидетельство Вход
Вход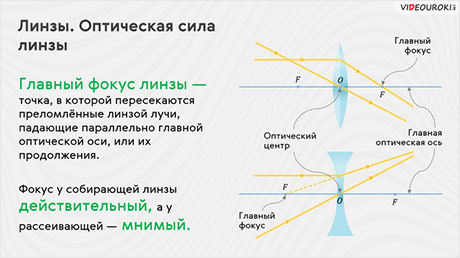




 5771
5771

