Возведение в квадрат суммы и разности двух выражений

Вопросы занятия:

·  вывести формулу квадрата суммы и разности двух выражений;

·  показать геометрическую иллюстрацию формулы квадрата суммы.

Материал урока

Нам известно, что при умножении многочлена на многочлен каждый член одного многочлена умножают на каждый член другого многочлена.

На этом уроке мы с вами поговорим, как в некоторых случаях упростить преобразования при умножении многочленов с помощью формул, которые называются формулами сокращённого умножения.

Давайте возведём в квадрат сумму:

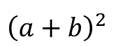
Представим это выражение в виде произведения двух многочленов

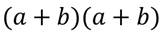
Выполним умножение

Приведём подобные слагаемые

Значит,

Это тождество называется формулой квадрата суммы.

Читается формула квадрата суммы так: квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого и второго выражений плюс квадрат второго выражения.

Посмотрите на рисунок, на котором геометрически проиллюстрирована формула квадрата суммы.

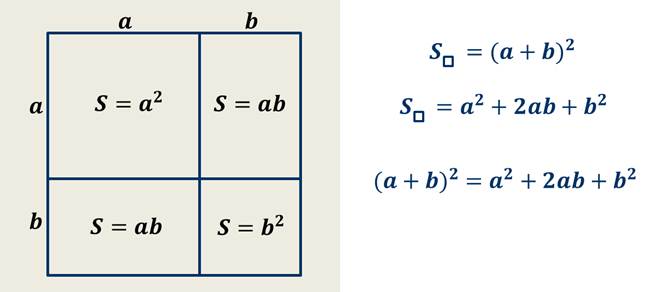
А это и есть формула квадрата суммы.

Теперь возведём в квадрат:

Представим это выражение в виде произведения

Выполним умножение

Приведем подобные слагаемые

Значит,

Это тождество называется формулой квадрата разности.

Читается формула квадрата разности так: квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого и второго выражений плюс квадрат второго выражения.

Теперь рассмотрим несколько примеров.

Пример.

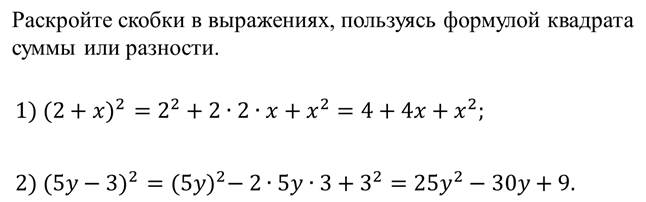
Пример.

Пример.