Вопросы:
· Определение циклического алгоритма.
· Виды циклов.
· Запись цикла с заданным условием продолжения работы.
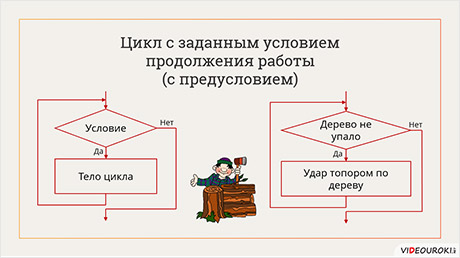
Итак, мы помним, что в разветвляющихся алгоритмах в зависимости от условия выполняется одна из двух последовательностей действий. Но часто возникает ситуация, когда от условия зависит количество исполнений некоторой последовательности действий. Например, лесоруб ударяет по дереву топором, до тех пор, пока оно не упадёт. Для описания таких ситуаций используются циклические алгоритмы.
Циклическими называются алгоритмы, которые содержат помимо прочих конструкцию повторения. Повторение (цикл) – это алгоритмическая конструкция, представляющая собой последовательность действий, которая выполняется многократно. Последовательность действий, исполняемых в цикле называется телом цикла.
Есть несколько способов организации повторений, в цикле. Так в зависимости от способов организации выделяют: циклы с заданным условием продолжения работы, циклы с заданным условием окончания работы и циклы с заданным числом повторений.
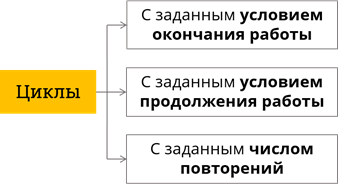
Виды организации цикла
Сегодня мы подробнее рассмотрим циклы с заданным условием продолжения работы (с предусловием).
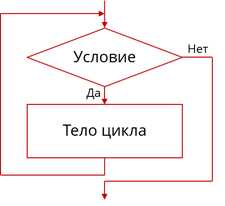
Блок-схема цикла с предусловием
Вспомним алгоритм действий лесоруба, который мы рассмотрели в начале урока. Его блок-схема соответствует циклу с заданным условием продолжения работы.
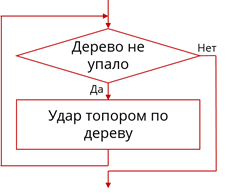
Блок-схема алгоритма действий лесоруба
На этом примере рассмотрим работу такого цикла. В начале проверяется условие цикла «Дерево не упало», которое, как и в ветвлении представляет собой логическое высказывание. Если это условие истинно – то выполняется тело цикла «Удар топором по дереву». После выполнения цикла снова проверяется его условие. Если оно истинно, то снова выполняется тело цикла. Так будет продолжаться до тех пор, пока выполняется условие цикла, то есть пока дерево не упало. Как только условие перестанет выполняться, то есть дерево упадёт, будут выполняться команды, расположенные после цикла.
Рассмотрим, как же записывается цикл с предусловием в языке Pascal. Для этого используется оператор цикла, который записывается служебным словом while. После этого слова через пробел записывается условие цикла, а после условия тоже через пробел записывается служебное слово do. На русский язык эту конструкцию можно перевести «Пока <условие> делай». На следующей строке, на расстоянии одного пробела от оператора цикла, будет следовать тело цикла. Оно состоит из серии операторов, записанных в порядке своего исполнения. Как правило они записываются в логических скобках, то есть между служебными словами begin и end. Если тело цикла состоит из одного оператора, то логические скобки записывать необязательно.
while <условие> do
begin
<оператор 1>;
<оператор 2>;
…
end;
Описание цикла с предусловием
Задача: Написать программу поиска наибольшего общего делителя двух целых положительных чисел по алгоритму Эвклида.
Как мы знаем, наибольшим общим делителем двух чисел называется набольшее число, на которое без остатка делятся оба числа.
Словесное описание алгоритма Эвклида: Пока числа не равны между собой – наибольшее из них заменяется разностью его самого и наименьшего числа. После чего выводится любое из них.
Составим блок-схему алгоритма. В начале пользователь вводит два целых числа, назовём их a и b. После этого следует условный блок a ≠ b. Если это условие выполняется – будет следовать ещё один условный блок, который будет определять из двух не равных чисел наибольшее. Его условием будет a > b. Если это условие выполняется, то переменной a мы должны присвоить значение разности a и b. В противном случае b будет больше a и переменной b мы присвоим значение b - a. После выполнения этого ветвления мы должны вернуться к условному блоку a ≠ b. Если условие этого блока не будет выполняться нам достаточно вывести на экран значение любой из переменных, например a.
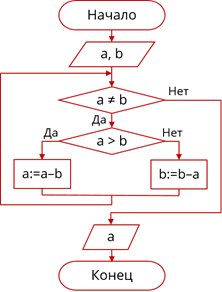
Блок-схема алгоритма
Напишем программу по составленной нами блок-схеме. Назовём её nod. Для решения задачи нам понадобятся две переменных, числа a и b. По условию задачи, это целые числа, поэтому переменные будут принадлежать к целочисленному типу integer. Запишем логические скобки. В начале будет следовать оператор writeln, который будет выводить поясняющее сообщение, что это программа расчёта НОД двух чисел и запрос на ввод двух чисел. Теперь запишем оператор readln (a, b). Дальше запишем оператор цикла с предусловием while. Его условие будет a<>b. Дальше будет следовать служебное слово do. Так как цикл будет содержать всего один условный оператор, логические скобки указывать не требуется. Запишем условный оператор if. Его условием будет a > b. После служебного слова then будет следовать оператор присваивания a:=a-b. Далее будет следовать служебное слово else. После него будет следовать оператор присваивания b:=b-a. После цикла достаточно написать оператор вывода значения переменной a.
program nod;
var
a, b: integer;
begin
writeln ('Программа расчёта НОД двух чисел. Введите два числа.');
readln (a, b);
while a<>b do
if a>b
then a:=a-b
else b:=b-a;
write ('НОД равен ', a);
end.
Исходный код программы
Запустим программу на выполнение. Введём числа 65 и 20. Их наибольший общий делитель действительно равен 5.

Программа работает верно. Задача решена.
Некоторые из вас могли заметить, что возможны случаи, когда алгоритм Эвклида будет работать медленно. Например, когда одно число во много раз больше другого. При числах 1 000 000 и 1, цикл в нашей программе повторится 999 999 раз. Поэтому появился усовершенствованный алгоритм Эвклида.
Словесное описание усовершенствованного алгоритма Эвклида: Пока оба числа не равно нулю, наибольшее из двух чисел заменяется остатком от деления себя на наименьшее число. После выполнения этих действий ненулевое число и будет равно значению НОД.
Изменим блок-схему алгоритма. Условие, записанное в первом условном блоке, изменится на a ≠ 0 и b ≠ 0. Ветви второго ветвления будут так же изменены. В них вместо разности переменным будут присваиваться остатки от деления их самих на другую переменную. Вывод ненулевого из чисел можно заменить выводом их суммы, так как одно из чисел всегда равно 0, значение суммы чисел будет равно ненулевому числу. Поэтому в блоке вывода в конце блок-схемы укажем a+b.
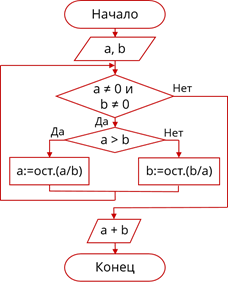
Блок-схема алгоритма
Изменим написанную нами программу. Для этого изменим условие цикла на (a<>0) and (b<>0). После слов then и else в операторах присваивания знаки минус заменим служебным словом mod, которым обозначается функция выделения остатка от деления. В операторе вывода в конце программы изменим a на a+b.
program nod;
var
a, b: integer;
begin
writeln ('Программа расчёта НОД двух чисел. Введите два числа.');
readln (a, b);
while (a<>0) and (b<>0) do
if a>b
then a:=a mod b
else b:=b mod a;
write ('НОД равен ', a+b)
end.
Изменённая программа
Снова запустим программу на выполнение и введём числа 740 и 222. Их наибольший общий делитель действительно 74.

Программа работает правильно. Задача решена.
Задача: Написать программу для перевода целых положительных чисел из десятичной системы счисления в двоичную. Мы помним алгоритм перевода числа из десятичной системы счисления в двоичную. Для этого достаточно число в десятичной системе счисления делить на два, и записывать остатки от деления пока оно не равно нулю. После чего вывести эти остатки от деления в порядке обратном записи.
Обозначим: с – число в десятичной системе счисления, строку s – число в двоичной системе счисления. Также нам понадобится промежуточная строка p.
Напишем программу для решения задачи. Назовём её DecToBin. В разделе описания переменных у нас будут переменные c типа integer, а также s и p типа string. Запишем логические скобки. В начале с помощью оператора writeln выведем на экран поясняющее сообщение о том, что это программа перевода чисел из десятичной системы счисления в двоичную и запрос на ввод числа. Далее будет следовать оператор readln (c). В начале программы строка Эс будет пуста, присвоим ей значение, не содержащее знаков. Теперь запишем цикл while c>0 do. Запишем логические скобки. После слова end будет следовать точка с запятой. В начале мы должны выделить остаток от деления c на 2 и добавить его в строку. Для перевода числовых значений в строковые есть функция str в скобках после соответствующего слова указывается числовое значение, в нашем случае c mod 2, и через запятую название строки, которой будет присвоен результат перевода в нашем случае p. Теперь нужно результат добавить в строку s. Так как цифры числа должны записываться в порядке обратном их нахождению, строке s присвоим результат Склейки строк p и s. Теперь присвоим переменной c результат её безостаточного деления на 2. После цикла с помощью оператора write выведем на экран поясняющее сообщение, что это введённое число в двоичной системе счисления и значение строки s.
program DecToBin;
var
c: integer;
s, p: string;
begin
writeln ('Программа перевода чисел из десятичной системы счисления в двоичную. Введите число в десятичной системе счисления.');
readln (c);
s:='';
while c>0 do
begin
str (c mod 2, p);
s:=p+s;
c:=c div 2;
end;
write ('Число в двоичной системе счисления: ', s);
end.
Исходный код программы
Запустим программу на выполнение. Введём число 255. В двоичной системе счисления это число действительно записывается 11111111.

Снова запустим программу и введём число 8. В двоичной системе это число действительно записывается 1000.

Программа работает правильно задача решена.
Важно запомнить:
· Циклическими называются алгоритмы, содержащие конструкцию повторения.
· Повторение (цикл) представляет собой последовательность действий, повторяющихся многократно.
· В зависимости от организации выделяют: циклы с заданным условием продолжения работы, циклы с заданным условием окончания работы и циклы с заданным числом повторений.

 Получите свидетельство
Получите свидетельство Вход
Вход




 12240
12240

