Вопросы:
· Различные способы записи ветвлений.
Задача: Написать программу, которая по номеру года определяет, сколько в нём дней.
Все годы делятся на високосные и не високосные. В первых – 366 дней, а в других – 365. Так задачу можно свести к определению того, является ли год, номер которого ввёл пользователь, високосным. Какие же годы являются високосными? Високосными называются годы, порядковые номера которых делятся на 4, но не делятся на 100, а также годы, номера которых делятся на 400.
Обозначим n – порядковый номер года и составим блок-схему алгоритма решения задачи. Сначала пользователь вводит порядковый номер года – n. Затем с помощью ветвления мы определим является ли введённый год високосным. Високосным является год, номер которого делится на 4, но не делится на 100, или же номер которого делится на 400. То есть остаток от деления n на 4 равен 0 и остаток от деления n на 100 не равен 0 или остаток от деления n на 400 равен 0. Если это условие выполняется – значит год високосный и в нём 366 дней. Программа должна вывести сообщение об этом. Если же условие не выполняется программа должна вывести сообщение о том, что в n-ном году 365 дней.
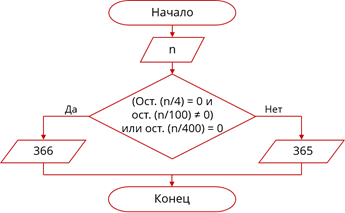
Блок-схема алгоритма
Напишем программу по составленной блок-схеме. Назовём её god. Для решения задачи нам потребуется всего одна переменная n. Так как это номер года, значит она может иметь только целое значение, то есть будет принадлежать к целому типу integer.
Запишем логические скобки. В начале программы будет следовать оператор writeln, который будет выводить на экран сообщение о том, что это программа определения количества дней в году. И запрос на ввод номера года. Затем будет следовать оператор readln (n). Теперь нужно проверить, является ли год високосным. Для этого запишем условный оператор. Операция нахождения остатка от деления записывается словом mod. То есть условием будет ((n mod 4=0) and (n mod 100<>0)) or (n mod 400=0). После слова Зэн будет следовать оператор write, который будет выводить на экран поясняющее сообщение о том, что в n-ном году 366 дней. После слова else будет следовать ещё один оператор write. Он будет выводить сообщение о том, что в n-ном году 365 дней.
program god;
var
n: integer;
begin
writeln ('Программа определения количества дней в году. Введите номер года.');
readln (n);
if ((n mod 4 = 0) and (n mod 100 <> 0)) or (n mod 400 = 0)
then write ('В ', n, ' году 366 дней.')
else write ('В ', n, ' году 365 дней.');
end.
Исходный код программы
Запустим программу на выполнение. Введём 368 год. Этот год действительно високосный и в нём 366 дней.

Снова запустим программу и введём 1900 год. Этот год действительно не является високосным, так как его номер делиться на 100. И в нём 365 дней.

Снова запустим программу и введём 2000 год. В этом году 366 дней, так как его номер делиться на 400.

И в последний раз запустим программу на выполнение. Введём 2007 год. В нём действительно 365 дней, так как его номер не делиться на 4.

Программа работает правильно. Задача решена.
Но эту же задачу можно решить и другим способом, используя вложенный условный оператор. Для этого условие того, что год високосный можно разбить на несколько частей. Сначала можно проверить, делиться ли номер года на 4. Если не делится, то в этом году 365 дней. Если же номер года делится на четыре – требуется дополнительная проверка. Условием этого ветвления возможность будет возможность безостаточного деления порядкового номера года на 100. Если условие не выполняется, то в этом году 366 дней. Если это условие выполняется, то нужна ещё проверка делимости номера года на 400. Если это условие выполняется – в таком году 366 дней. В противном случае – 365.
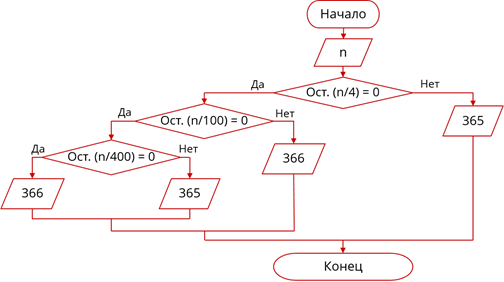
Блок-схема алгоритма
Изменим написанную нами программу, по изображённой блок-схеме определения високосного года. Удалим условный оператор. И запишем новый с условием: n mod 4=0. После слова then будет следовать условный оператор с условием: n mod 100=0. Если это условие будет выполняться, то дальше следует ещё один условный оператор с условием: n mod 400=0. После слова then в нём будет следовать оператор write, который выводит поясняющее сообщение о том, что в n-ном году 366 дней. После слова else будет следовать ещё один оператор write, который будет выводить на экран сообщение о том, что в n-ном году 365 дней. Просто скопируем предыдущий оператор вывода и далее будем вставлять его копию и изменять в ней количество дней. Далее будет следовать слово else для оператора с условием: n mod 100=0. После него будет следовать оператор write, который выведет на экран сообщение о том, что в n-ном году 366 дней. Далее будет следовать служебное слово else для оператора с условием: n mod 4=0. После него будет следовать оператор write, который будет выводить сообщение о том, что в n-ном году 365 дней. После него будет следовать точка с запятой.
program god;
var
n: integer;
begin
writeln ('Программа определения количества дней в году. Введите номер года.');
readln (n);
if n mod 4 = 0
then if n mod 100 = 0
then if n mod 400 = 0
then write ('В ', n, ' году 366 дней.')
else write ('В ', n, ' году 365 дней.')
else write ('В ', n, ' году 366 дней.')
else write ('В ', n, ' году 365 дней.');
end.
Исходный код программы
Запустим программу на выполнение и используем для проверки те же тесты, что и в первый раз.




Сравним исходные коды первоначальной и изменённой программ. Видно, что текст первоначальной программы короче. Однако, так как во втором варианте условие разбито на несколько более простых составляющих, для некоторых, этот вариант может показаться более понятным. В двух алгоритмах проверяются одни и те же условия, просто во втором варианте они разбиты на несколько условных операторов, то есть принцип работы у обеих программ будет один и тот же, поэтому и скорость работы у них будет приблизительно одинаковой.
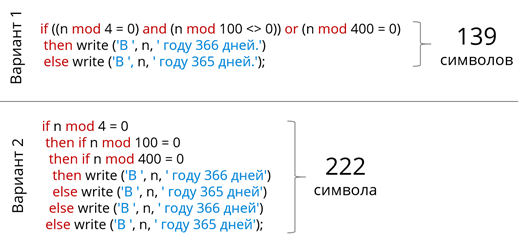
Сравнение вариантов программы
Задача: Точка на плоскости задана своими координатами x и y. Определить в какой координатной четверти лежит заданная точка, если её координаты не равны нулю.
Изобразим координатную плоскость и вспомним, как располагаются координатные четверти. Сверху и справа от начала отсчёта располагается первая координатная четверть. Остальные располагаются по возрастанию против часовой стрелки. Таким образом, для того, чтобы точка располагалась в I координатной четверти обе её координаты должны быть положительными. Во II четверти координата x будет отрицательной, а y – положительной. В III четверти обе координаты будут отрицательными. В IV четверти координата х точки будет положительной, а y – отрицательной.
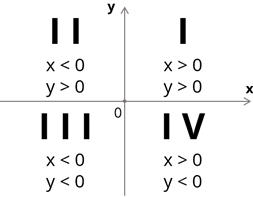
Составим блок схему алгоритма решения этой задачи. В начале работы программы пользователь вводит с клавиатуры координаты точки: x и y. Потом будет следовать ветвление с условием принадлежности точки к I координатной четверти, то есть x > 0 и y > 0. Если это условие будет выполняться – выведем на экран сообщение о том, что точка принадлежит к I координатной четверти. Если условие не будет выполняться – ничего делать не нужно. Далее будет следовать ветвление, с условием принадлежности точки к II координатной четверти, то есть x < 0 и y > 0. Если это условие будет выполняться – выведем на экран поясняющее сообщение о том, что точка принадлежит к II координатной четверти, если это условие не выполняется – ничего делать не нужно. Далее будут следовать такие же условные операторы, определяющие принадлежность точки к третьей и четвёртой координатным четвертям.
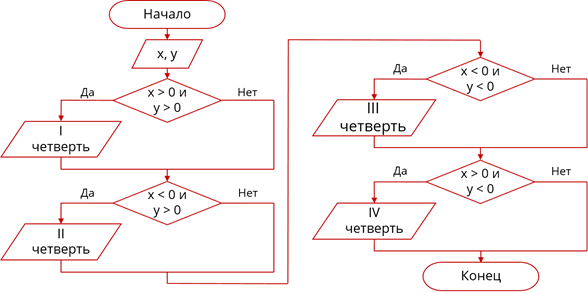
Блок-схема алгоритма
Напишем программу по составленной блок-семе. Назовём её tochka. Для решения задачи нам потребуется две переменные, которые будут хранить координаты точки: x и y. Так как в условии задачи не сказано, что координаты целые, укажем эти переменные вещественного типа real.
Запишем логические скобки. В начале запишем оператор writeln Который выводит на экран сообщение о том, что это программа, определяющая, в какой координатной четверти лежит точка и запрос на ввод координат точки. Далее будет следовать оператор readln (x, y). За ним будут следовать условные операторы, определяющие принадлежность точки к координатной четверти. Запишем первый из них. Его условием будет (x>0) and (y>0). После слова then будет следовать оператор write. Он будет выводить на экран поясняющее сообщение о том, что точка принадлежит к I координатной четверти. После него будет следовать точка с запятой. Так как условные операторы, определяющие принадлежность точки к координатным четвертям, будут похожи, скопируем первый из них, и в дальнейшем будем вставлять его изменять. После того, как мы вставили оператор в первый раз, изменим его условие, на соответствующее II координатной четверти, то есть (x<0) and (y>0). А в выводимом на экран сообщении изменим номер четверти на II. Ещё раз вставим скопированный условный оператор и изменим условие на (x<0) and (y<0). В выводимом сообщении изменим номер четверти на III. И снова вставим скопированный условный оператор. Изменим его условие на (x>0) and (y<0), а в выводимом сообщении, номер четверти – на IV.
program tochka;
var
x, y: real;
begin
writeln ('Программа определения того, в какой координатной четверти лежит точка. Введите координаты точки.');
readln (x, y);
if (x>0) and (y>0)
then write ('Точка лежит в I координатной четверти.');
if (x<0) and (y>0)
then write ('Точка лежит во II координатной четверти.');
if (x<0) and (y<0)
then write ('Точка лежит в III координатной четверти.');
if (x>0) and (y<0)
then write ('Точка лежит в IV координатной четверти.');
end.
Исходный код программы
Запустим программу на выполнение. Введём координаты точки (1; 1). Точка с этими координатами действительно принадлежит к I координатной четверти.
Снова запустим программу и введём координаты (-2; 3). Точка с этими координатами действительно принадлежит ко II координатной четверти.

Снова запустим программу и введём координаты (-5; -1). Эта точка находится в III четверти.

В последний раз запустим программу на выполнение и введём координаты (1; -7). Эта точка действительно в IV четверти.

Программа работает правильно. Задача решена.
Эту же задачу можно решать и по-другому. Сначала можно разделить координатную плоскость на 2 части, например верхнюю и нижнюю. Условием принадлежности к верхней полуплоскости будет положительная координата y. Если эта координата будет отрицательной, то точка будет принадлежать к нижней полуплоскости. Определив, к какой полуплоскости принадлежит точка, проще определить в какой она лежит четверти. Находясь в верхней полуплоскости и имея положительную координату x, точка находится в I координатной четверти, при отрицательной координате x, точка находится во II четверти. Также можно определить принадлежность точки к III или IV четверти.
Изменим, написанную нами программу. Для этого удалим написанные нами условные операторы. Вместо них запишем условный оператор, который определяет к какой полуплоскости принадлежит точка. Его условием будет y>0. Если это условие будет выполняться, то точка находится в верхней полуплоскости. Дальше будет следовать ещё один условный оператор с условием: x>0. Если это условие будет выполняться выведем на экран монитора поясняющее сообщение о том, что точка принадлежит к I координатной четверти, если условие выполнять не будет, то точка принадлежит ко II координатной четверти. Если условие y>0 не будет выполняться, то точка находится в нижней полуплоскости и далее будет следовать условный оператор с условием: x>0. Если это условие будет выполняться, то точка будет находится в IV четверти. Если это условие не будет выполняться, то точка будет в III четверти.
program tochka;
var
x, y: real;
begin
writeln ('Программа определения того, в какой координатной четверти лежит точка. Введите координаты точки.');
readln (x, y);
if y>0
then if x>0
then write ('Точка лежит в I координатной четверти.')
else write ('Точка лежит во II координатной четверти.')
else if x>0
then write ('Точка лежит в IV координатной четверти.')
else write ('Точка лежит в III координатной четверти.')
end.
Исходный код программы
Запустим программу на выполнение и зададим те же координаты точек, что и в первой программе.




Сравним различные части вариантов программы. Возможно первый вариант вам покажется нагляднее, так как каждой координатной четверти соответствует отдельный условный оператор. Однако условия в этих условных операторах состоят из двух простых логических высказываний. И если точка принадлежит к IV координатной четверти, то программа определит это только на четвёртом условном операторе. Условия в условных операторах второго варианта состоят из одного простого высказывания и для того, чтобы определить в какой координатной четверти находится точка работает всегда два условных оператора, внешний и один из вложенных. Внешний определяет полуплоскость, в которой находится точка, а вложенный – координатную четверть. Значит второй вариант программы будет работать быстрее.

Сравнение вариантов программы
Важно запомнить:
· Разветвляющиеся алгоритмы для решения одних и тех же задач могут быть записаны по-разному. Это связано с тем, что сложные логические высказывания можно разбивать на более простые.
· У различных программ для решения одной и той же задачи может изменяться размер исходного кода и скорость выполнения.

 Получите свидетельство
Получите свидетельство Вход
Вход





 2932
2932

