С помощью простых опытов мы показали, что в однородной среде свет распространяется прямолинейно. Если же пучок света падает на границу раздела двух однородных прозрачных сред, то часть его отражается и возвращается в первоначальную среду. При этом падающий луч, отражённый луч и нормаль к отражающей поверхности в точке падения луча лежат в одной плоскости. А угол отражения равен углу падения.
Также мы с вами смогли доказать закон отражения света с помощью принципа Гюйгенса, согласно которому, каждая точка волнового фронта является источником вторичных сферических волн. Огибающая поверхность к фронтам волн от вторичных источников определяет положение нового фронта волны.
Однако, свет, падая на границу раздела двух сред, не только отражается от неё, но и частично проходит во вторую среду и распространяется в ней. Явление изменения направления распространения света при его переходе из одной среды в другую называется преломлением света.
Интересно, что первые упоминания о преломлении света в воде и стекле встречаются в труде Клавдия Птолемея «Оптика», вышедшем в свет во II в. н. э..
Давайте вспомним некоторые понятия и законы, связанные с данным явлением. Для этого обратимся к простому опыту: укрепим в центре оптического диска тонкую стеклянную пластинку и направим на неё узкий пучок света. Как видим, небольшая часть света отразилась от пластинки, а часть света прошла сквозь неё, изменив при этом своё направление распространения.
Проведём перпендикуляр к границе раздела двух сред в точке падения луча и вспомним, что луч света, идущий к границе раздела двух сред, называется падающим лучом. А угол между падающим лучом и перпендикуляром, восста́вленным в точке падения луча, называется углом падения.

Луч же света, проходящий во вторую среду, называется преломлённым лучом. Следовательно, угол между перпендикуляром, восставленным к границе раздела двух сред в точке падения луча, и преломлённым лучом называется углом преломления.
Здесь же отметим, что если свет падает перпендикулярно на границу раздела двух сред, то он не испытывает преломления. Разумеется, не будет преломления и на границе, разделяющей две среды с одинаковыми физическими свойствами.
Сравним углы падения и преломления. Как видно, угол преломления меньше угла падения. Увеличим угол падения — угол преломления тоже увеличивается, но по-прежнему он меньше угла падения. А то, что мы на оптическом диске видим не только падающий луч, но и преломлённый, говорит о том, что они оба лежат в одной плоскости — плоскости диска. На основании вышесказанного мы можем с вами сформулировать первую часть закона преломления света. Итак, падающий луч, преломлённый луч и нормаль к границе раздела двух сред в точке падения луча лежат в одной плоскости.
Чтобы сформулировать вторую часть закона преломления рассмотрим падение плоской световой волны на плоскую поверхность раздела однородных изотропных и прозрачных сред при условии, что размеры поверхности раздела намного больше длины волны падающего излучения. Если угол падения отличен от нуля, то различные точки фронта волны достигнут границы раздела двух сред не одновременно.
Пусть фронт волны перемещается в первой среде со скоростью, модуль которой мы обозначим через υ1. Тогда в точке В колебания начнут возбуждаться с запаздыванием по времени на величину СВ/υ1.

В момент времени, когда волна достигнет точки B и в этой точке начнётся возбуждение колебаний, вторичная волна с центром в точке A уже будет представлять собой полусферу радиусом υ2Δt, где υ2 — это скорость распространения света во второй по ходу луча среде. Радиусы вторичных волн от источников, расположенных между точками A и B, меняются так, как показано на экране.
Огибающей вторичных волн является плоскость BD — касательная к сферическим поверхностям. Она представляет собой волновую поверхность преломлённой волны. При этом преломлённые лучи АА2 и BB2 перпендикулярны этой поверхности.
Давайте посмотрим на ΔАВС — он у нас прямоугольный
по построению. Следовательно, угол  равен
углу падения луча АА1, как углы со взаимно перпендикулярными
сторонами. Тогда длину стороны ВС можно найти:
равен
углу падения луча АА1, как углы со взаимно перпендикулярными
сторонами. Тогда длину стороны ВС можно найти:

Теперь рассмотрим ΔАВD — он тоже прямоугольный по построению. При этом угол  равен углу
преломления, как углы между двумя взаимно перпендикулярными сторонами. Поэтому
равен углу
преломления, как углы между двумя взаимно перпендикулярными сторонами. Поэтому

Разделим почленно последние два уравнения друг на друга и упростим полученное равенство:

Отношение  называют относительным
показателем преломления. Он показывает, во сколько раз скорость света в первой
походу луча среде отличается от скорости распространения света во второй среде:
называют относительным
показателем преломления. Он показывает, во сколько раз скорость света в первой
походу луча среде отличается от скорости распространения света во второй среде:

Чем он больше, тем сильнее преломляется свет на границе раздела двух сред.

Таким образом, отношение синуса угла падения к синусу угла преломления есть величина постоянная для данных двух сред, равная относительному показателю преломления второй среды относительно первой:

Это есть вторая часть закона преломления света, экспериментально установленная в 1620 году голландским учёным Виллебродом Снеллом. Однако эти результаты им опубликованы не были. Лишь в 1637 году (уже после смерти учёного) они были обнаружены в архивах математиком Рене Декартом, который использовал их при написании своих «Рассуждений о методе ...» в приложении «Диоптрика» (хотя некоторые историки склоняются к тому, что Декарт самостоятельно переоткрыл закон преломления света).
Из закона преломления света видно, что различие углов падения и преломления обусловлено тем, что скорость распространения света в различных средах различна. Следовательно, будет различна и длина световой волны. Однако, что очень важно, что при преломлении частота света остаётся неизменной.

Принято считать, что чем больше скорость распространения света в среде, тем меньше её оптическая плотность и наоборот. При этом если пучок света переходит из среды оптически менее плотной в среду оптически более плотную, то угол преломления меньше угла падения (преломлённый луч как бы прижимается к перпендикуляру). А если свет переходит из среды оптически более плотной в среду оптически менее плотную, то угол преломления больше угла падения (преломлённый луч как бы прижимается к границе раздела сред). Кстати, этот вывод логически следует из свойства обратимости, которое характерно не только для падающего и отражённого, но и для падающего и преломлённого лучей.
Если свет падает из вакуума в вещество, то вводится величина, называемая абсолютным показателем преломления. Он показывает, во сколько раз скорость света в вакууме больше, чем в данной среде.
С помощью закона преломления света можно рассчитать ход лучей в различных оптических устройствах, например в треугольной призме, изготовленной из какого-либо прозрачного материала. На экране вы видите сечение треугольной стеклянной призмы плоскостью, перпендикулярной её боковым рёбрам. Пусть монохроматический свет (то есть свет строго определённой частоты) падает на грань призмы, находящейся в воздухе. Так как свет переходит из среды оптически менее плотной в оптически более плотную, то угол преломления меньше угла падения. Пройдя через призму, свет падает на её вторую грань. Здесь он снова преломляется, но теперь угол падения меньше угла преломления.
Грани, на которых происходит преломление света, называются преломляющими гранями.
Угол между преломляющими гранями называется преломляющим углом призмы.
Угол, образованный направлением луча, входящего в призму, и направлением луча, выходящего из неё, называют углом отклонения.
А грань, лежащая против преломляющего угла, называется основанием призмы.

В заключении отметим, что в настоящее время существуют материалы с отрицательным показателем преломления. Их называют метаматериалами. В большинстве случаев их история начинается с упоминания работы советского физика Виктора Григорьевича Веселаго, опубликованной в журнале «Успехи физических наук» в 1967 году.

Существование подобных материалов было доказано в 2000 году англичанином Джоном Пендри и американцем Дэвидом Смитом. Одно из возможных свойств метаматериалов — это отрицательный (или левосторонний) показатель преломления, который проявляется при одновременной отрицательности диэлектрической и магнитной проницаемостей среды.

 Получите свидетельство
Получите свидетельство Вход
Вход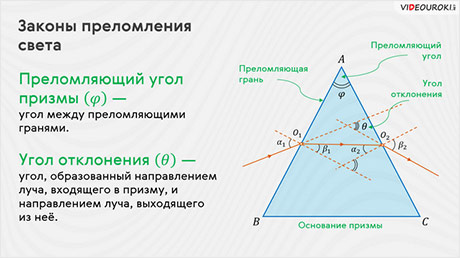




 5542
5542

