Работа силы

Все мы с детства знаем, что такое физическая работа. Самые элементарные действия, такие как, пододвинуть стол или нести рюкзак — это та или иная работа. И на эту работу, как мы говорим, нужно затратить силы.

Работа силы — это величина, характеризующая воздействие силы, в зависимости как от самой силы, так и от перемещения тела, к которому была приложена сила.

Мы, наверняка скажем, что нести рюкзак целый километр вдвое тяжелее, чем нести этот же рюкзак всего полкилометра. Хотя для того, чтобы удержать рюкзак на спине требуется одна и та же сила, не зависимо от расстояния, которое вы преодолеете.

Таким образом, работа силы в механике равна произведению силы и перемещения тела, к которому была приложена сила:

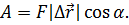
Напомним, что и сила, и перемещение являются векторными величинами. Если направление силы, вызвавшей перемещение, не совпадает с направлением самого перемещения, то работа определяется как произведение модуля силы, модуля перемещения и косинуса угла между направлением силы и направлением перемещения.

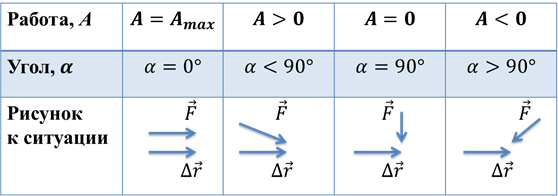
Поскольку косинус любого угла не может быть больше единицы, и косинус 0^о равен единице, можно заключить, что максимальная работа выполняется тогда, когда сила приложения направлена так же, как и перемещение. Это хорошо подтверждается и бытовыми наблюдениями.

 Если же, напротив, сила, приложенная к телу, перпендикулярна его перемещению, то работа этой силы равна нулю. Действительно: как бы мы сильно ни воздействовали на то или иное тело, это воздействие не может привести к его движению в направлении, перпендикулярном приложенной силе.

Поскольку косинус принимает отрицательные значения, если аргумент больше, чем 90^о, в этом случае, работа будет отрицательной. Ярким примером такой работы является работа силы трения, о которой мы в отдельности поговорим чуть позже. Ведь сила трения препятствует движение, а, значит, совершает отрицательную работу.

Заметим, что работа, сама по себе, не может быть куда-либо направлена, хотя и определяется с помощью векторных величин. Поэтому, работа является скалярной величиной.

Если на тело действуют несколько сил, то сумма работ всех сил равна работе равнодействующей силы.

Единицей измерения работы является джоуль: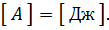

1 Дж — это работа, совершаемая силой 1 Н на перемещении 1 м, при условии, что направление этой силы совпадает с направлением перемещения.

Можно привести множество примеров совершения механической работы. Например, если человек двигает шкаф, то он совершает работу. Чем бо́льшую силу он прикладывает, и чем больше перемещает шкаф, тем бо́льшую работу он совершает. Лошадь может тянуть телегу с постоянной скоростью, но чем дальше телега уедет, тем бо́льшую работу совершит лошадь.

Необходимо отметить, что разделяется два вида работы: полезная работа и работа совершенная. Рассмотрим простой пример: один мальчик прошел 10 м, а другой — 5 м и вернулся обратно. Допустим, что оба мальчика затрачивают одинаковую силу на перемещения. При этом оба они прошли 10 м, а, значит, фактически совершили одинаковую работу. Но, вот полезная работа мальчика, который вернулся в исходную, точку равна нулю, поскольку его перемещение равно нулю. Мальчик затратил силы, но добился «нулевого результата»: его положение никак не изменилось.

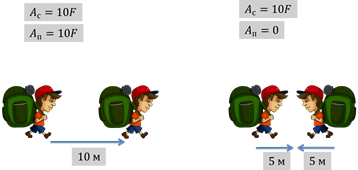
Так вот, в механике, говоря о работе силы, имеют ввиду полезную работу.

Примеры решения задач.

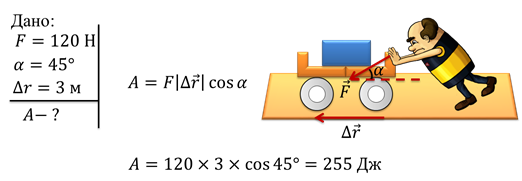
Задача 1. Человек толкнул телегу, приложив силу под углом 45° к горизонту. Модуль этой силы равен 120 Н. Пренебрегая трением, определите работу силы, приложенной человеком, если тележка проехала 3 м в горизонтальном направлении?

Задача 2. При растяжении пружины на 70 см, работа силы упругости составляет 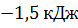. Найдите коэффициент жесткости этой пружины.

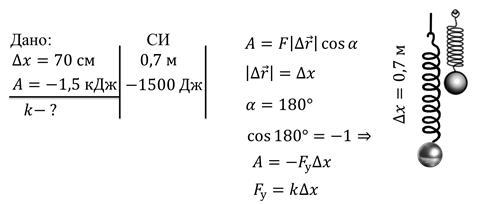
И тут у нас возникает сложность: ведь сила упругости, как мы помним, зависит от того, насколько сильно растянули пружину, поэтому, мы не можем найти силу упругости, просто разделив работу на перемещение. Тем не менее, зависимость силы упругости от растяжения является линейной, а, следовательно, график зависимости силы упругости от растяжения будет являться прямой линией. Если мы построим такой график, то убедимся, что площадь под ним будет равна работе силы упругости.